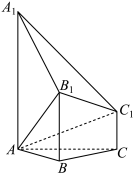
如图,已知多面体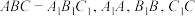 均垂直于平面
均垂直于平面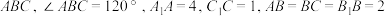 .
.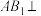 平面
平面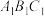 ;
;
(Ⅱ)求直线 与平面
与平面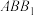 所成角的正弦值.
所成角的正弦值.
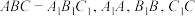 均垂直于平面
均垂直于平面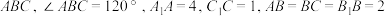 .
.
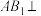 平面
平面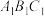 ;
;(Ⅱ)求直线
 与平面
与平面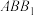 所成角的正弦值.
所成角的正弦值.
2018·浙江·高考真题 查看更多[80]
山东省青岛第二中学2024届高三下学期二模考试数学试题浙江省天域全国名校协作体2023-2024学年高三二模数学试题(已下线)期中真题必刷压轴60题(18个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)四川省自贡市第二十二中学校2023-2024学年高二上学期期中数学试题河南省洛阳复兴学校2023-2024学年高二上学期期中考试数学模拟试题(已下线)陕西省西安市铁一中学2023-2024学年高三上学期第一次月考理科数学试题陕西省西安市铁一中学2023-2024学年高三上学期9月月考理科数学试题陕西省西北工业大学咸阳启迪中学2022-2023学年高二下学期第一次月考理科数学试题陕西省延安市子长市中学2020-2021学年高二下学期期中理科数学试题福建省福州市四校联盟(永泰城关中学、连江文笔中学、长乐高级中学、元洪中学)2022-2023学年高二上学期期末联考数学试题(已下线)专题24 空间向量与空间角的计算-十年(2011-2020)高考真题数学分项(已下线)专题8.5 直线、平面垂直的判定及其性质(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题8.7 立体几何中的向量方法(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题8.7 立体几何中的向量方法(练)【理】-《2020年高考一轮复习讲练测》广西梧州市藤县第六中学2021-2022学年高二上学期期末热身考试数学(理)试题(已下线)专题07 点线面的位置关系安徽省六安实验中学2022-2023学年高三上学期第五次质量检测数学试题广东省深圳市宝安中学2022-2023学年高二上学期期中数学试题四川省成都市树德中学2021-2022学年高一下学期期末考试数学试题河北省博野中学2021-2022学年高二上学期期末数学试题上海市大同中学2022届高三下学期开学考试数学试题(已下线)专题26空间向量与空间角的计算-2022年高三毕业班数学常考点归纳与变式演练(理科专用)广东省佛山市第三中学2021-202学年高二上学期第一次教学质量检测数学试题(已下线)第37讲 立体几何中的向量方法 (讲) — 2022年高考数学一轮复习讲练测(课标全国版)(已下线)专题01 通过空间向量解决立体几何中的角度问题(解答题专练)-【重难点突破】2021-2022学年高二数学上册常考题专练(人教A版2019选择性必修第一册)(已下线)专题10 立体几何-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)专题07 空间向量与立体几何-十年(2012-2021)高考数学真题分项汇编(浙江专用)江苏省南通市如皋中学2020-2021学年高一(创新班)下学期第二次阶段考试数学试题安徽省六安市舒城中学2020-2021学年高二下学期开学考试数学(文)试题(已下线)专题19 立体几何综合-2020年高考数学母题题源全揭秘(浙江专版)(已下线)押第19题立体几何-备战2021年高考数学临考题号押题(浙江专用)(已下线)技巧03 解答题解法与技巧 第二篇 解题技巧篇(练)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)专题4.4 空间向量与立体几何-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)思想04 化归与转化思想 第三篇 思想方法篇(练)-2021年高考二轮复习讲练测(浙江专用)江苏省盐城市阜宁县2020-2021学年高二上学期期末数学试题(已下线)专题8.5 直线、平面垂直的判定及性质(精讲)-2021年高考数学(理)一轮复习学与练(已下线)专题12 点线面的位置关系与空间的角-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)专题8.5 直线、平面垂直的判定及性质 (精讲)-2021年高考数学(文)一轮复习学与练(已下线)练习7+点线面的位置关系-2020-2021学年【补习教材·寒假作业】高一数学(人教A版)山西省长治市第二中学校2020-2021学年高二上学期期中数学(文)试题山西省长治市第二中学校2020-2021学年高二上学期期中数学(理)试题(已下线)考点32 直线、平面垂直的判定及其性质-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题8.5 直线、平面垂直的判定及性质 (精讲)-2021年高考数学(文)一轮复习讲练测(已下线)专题8.5 直线、平面垂直的判定及性质 (精讲)-2021年高考数学(理)一轮复习讲练测(已下线)专题8.7 利用空间向量求空间角 (精讲)--2021年高考数学(理)一轮复习讲练测(已下线)专题8.3 空间点、直线、平面之间的位置关系(讲)-2021年新高考数学一轮复习讲练测湖北省宜昌市夷陵中学、荆门市钟祥一中两校2020-2021学年高二上学期10月联考数学试题(已下线)【新东方】杭州新东方高中数学试卷339上海市复旦大学附属中学青浦分校2020届高三下学期开学摸底数学试题人教B版(2019) 选择性必修第一册 过关斩将 第一章 空间向量与立体几何 1.1-1.2 综合拔高练江苏省南通市2019-2020学年高二下?学期期末数学试题(B卷)(已下线)专题17 立体几何综合-五年(2016-2020)高考数学(理)真题分项(已下线)专题06 立体几何(解答题)——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题17 立体几何综合-五年(2016-2020)高考数学(文)真题分项(已下线)专题06 立体几何(解答题)——三年(2018-2020)高考真题理科数学分项汇编山西省大同市第一中学2019-2020学年高二下学期3月网上考试数学(理)试题2020届江西省赣州市赣县三中高三1月考前适应性考试数学(理)试题江西省赣州一中2019-2020学年度高二下学期月考数学(理科)试题人教A版(2019) 必修第二册 突围者 第八章 模拟高考检测专题21 空间向量与几何体-《巅峰冲刺2020年高考之二轮专项提升》[江苏](已下线)专题8.5 直线、平面垂直的判定及其性质(练)-江苏版《2020年高考一轮复习讲练测》(已下线)专题8.5 直线、平面垂直的判定及其性质(讲)-江苏版《2020年高考一轮复习讲练测》(已下线)专题8.7 立体几何中的向量方法(讲)-浙江版《2020年高考一轮复习讲练测》(已下线)专题8.3 空间点、直线、平面之间的位置关系(讲)-浙江版《2020年高考一轮复习讲练测》(已下线)专题8.5 直线、平面垂直的判定及其性质(讲)【理】-《2020年高考一轮复习讲练测》湖南省长沙市宁乡一中2019-2020学年高一(拓展班)上学期11月月考数学试题(已下线)专题8.5 直线、平面垂直的判定及其性质(练)【文】-《2020年高考一轮复习讲练测》(已下线)专题8.5 直线、平面垂直的判定及其性质(讲)【文】-《2020年高考一轮复习讲练测》2019年上海市大同中学高三下学期5月三模数学试题步步高高二数学暑假作业:【理】作业13 空间向量及其应用【全国百强校】山西省长治市第二中学2018-2019学年高二上学期期中考试数学(理)试题【全国百强校】河北省武邑中学2019届高三上学期第二次调研考试数学(理)试题【全国百强校】山西省临汾第一中学2018-2019学年高二10月月考数学(文)试题(已下线)2018年10月18日 《每日一题》一轮复习(文数)-空间角与距离(1)【省级联考】湖南湖北八市十二校2019届高三第一次调研联考文科数学试题(已下线)2018年10月12日 《每日一题》一轮复习理数-空间角与距离(1)(已下线)2017-2018学年度下学期高中期末备考 【浙江版】高二【精准复习模拟题】 拔高卷01【教师版】(已下线)2018年高考题及模拟题汇编 【文科】5.立体几何(已下线)2018年高考题及模拟题汇编 【理科】5.立体几何2018年全国普通高等学校招生统一考试数学(浙江卷)
更新时间:2018-06-09 15:18:53
|
相似题推荐
解答题-证明题
|
适中
(0.65)
名校
【推荐1】如图,菱形ABCD中, ,
,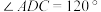 ,O为线段CD的中点,将
,O为线段CD的中点,将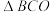 沿BO折到
沿BO折到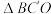 的位置,使得
的位置,使得 ,E为
,E为 的中点.
的中点.
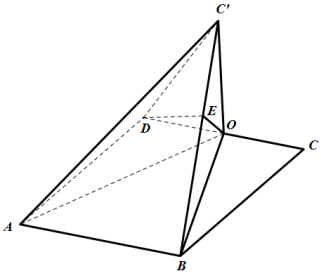
(1)求证: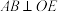 ;
;
(2)求直线AE与平面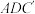 所成角的正弦值
所成角的正弦值
 ,
,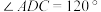 ,O为线段CD的中点,将
,O为线段CD的中点,将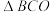 沿BO折到
沿BO折到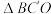 的位置,使得
的位置,使得 ,E为
,E为 的中点.
的中点.
(1)求证:
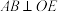 ;
;(2)求直线AE与平面
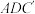 所成角的正弦值
所成角的正弦值
您最近半年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐2】如图,在四棱锥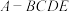 中,
中,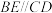 ,
,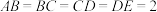 ,
,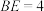 ,
, .
.
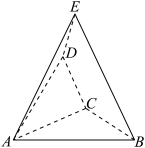
(1)求证: .
.
(2)若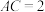 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
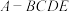 中,
中,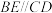 ,
,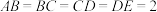 ,
,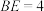 ,
, .
.
(1)求证:
 .
.(2)若
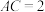 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近半年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐3】如图,在正方体 中,棱长为1,
中,棱长为1,

(1)求证: 平面
平面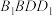 ;
;
(2)求平面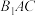 和平面
和平面 的夹角的余弦值.
的夹角的余弦值.
 中,棱长为1,
中,棱长为1,
(1)求证:
 平面
平面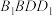 ;
;(2)求平面
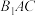 和平面
和平面 的夹角的余弦值.
的夹角的余弦值.
您最近半年使用:0次
解答题-证明题
|
适中
(0.65)
名校
【推荐1】如图,在四棱锥 中,
中, 平面
平面 ,
,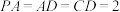 ,
,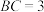 ,
, ,
, 为
为 中点,
中点, .
.
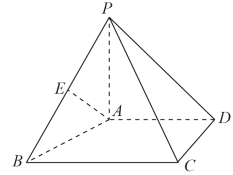
(1)求证:BC//平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, 平面
平面 ,
,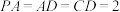 ,
,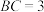 ,
, ,
, 为
为 中点,
中点, .
.
(1)求证:BC//平面
 ;
;(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近半年使用:0次
解答题-问答题
|
适中
(0.65)
名校
解题方法
【推荐2】在三棱柱 中,
中, 平面
平面 ,
, ,
, 分别是
分别是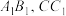 的中点.
的中点.
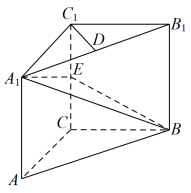
(1)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)在棱 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成锐二面角为
所成锐二面角为 ?若存在,确定
?若存在,确定 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
 中,
中, 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点. 
(1)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(2)在棱
 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成锐二面角为
所成锐二面角为 ?若存在,确定
?若存在,确定 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
您最近半年使用:0次

 ,
, ,
, ,
, 为
为 的中点,
的中点, 的中点,
的中点, 为
为 的中点.
的中点.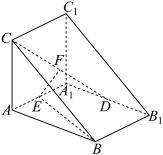
 所成角的正弦值;
所成角的正弦值; 与平面
与平面

