名校
1 . 对两个变量 和
和 进行回归分析,得到一组样本数据
进行回归分析,得到一组样本数据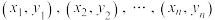 ,下列统计量的数值能够刻画其经验回归方程的拟合效果的是( )
,下列统计量的数值能够刻画其经验回归方程的拟合效果的是( )
 和
和 进行回归分析,得到一组样本数据
进行回归分析,得到一组样本数据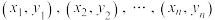 ,下列统计量的数值能够刻画其经验回归方程的拟合效果的是( )
,下列统计量的数值能够刻画其经验回归方程的拟合效果的是( )| A.平均数 | B.相关系数 | C.决定系数 | D.方差 |
您最近半年使用:0次
今日更新
|
1050次组卷
|
3卷引用:湖南省九校联盟2024届高三下学期第二次联考数学试题
2 . 若干人独立地向一游动目标射击,每人击中目标的概率都是0.6,若要以0.97以上的概率击中目标,则至少需要的人数是( )
| A.6 | B.5 | C.4 | D.3 |
您最近半年使用:0次
名校
3 . 某商场举行“庆元宵,猜谜语”的促销活动,抽奖规则如下:在一个不透明的盒子中装有若干个标号为1,2,3的空心小球,球内装有难度不同的谜语.每次随机抽取2个小球,答对一个小球中的谜语才能回答另一个小球中的谜语,答错则终止游戏.已知标号为1,2,3的小球个数比为1:2:1,且盒中2号球的个数为4.
(1)求取到异号球的概率;
(2)若甲抽到1号球和3号球,甲答对球中谜语的概率和对应奖金如表所示,请帮甲决策猜谜语的顺序(猜对谜语的概率相互独立)
(1)求取到异号球的概率;
(2)若甲抽到1号球和3号球,甲答对球中谜语的概率和对应奖金如表所示,请帮甲决策猜谜语的顺序(猜对谜语的概率相互独立)
球号 | 1号球 | 3号球 |
答对概率 | 0.8 | 0.5 |
奖金 | 100 | 500 |
您最近半年使用:0次
4 . 从1到7这7个数字中取2个偶数、3个奇数,排成一个无重复数字的五位数.求:
(1)共有多少个五位数?
(2)其中偶数排在一起,奇数也排在一起的有多少个?
(3)其中两个偶数不相邻的有多少个?
(1)共有多少个五位数?
(2)其中偶数排在一起,奇数也排在一起的有多少个?
(3)其中两个偶数不相邻的有多少个?
您最近半年使用:0次
5 . 若m,n为正整数且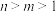 ,则( )
,则( )
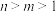 ,则( )
,则( )A. | B.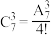 |
C. | D.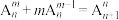 |
您最近半年使用:0次
名校
解题方法
6 . 已知随机变量X,Y满足 ,且随机变量X的分布列如图:则随机变量Y的方差
,且随机变量X的分布列如图:则随机变量Y的方差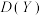 等于
等于________ .
 ,且随机变量X的分布列如图:则随机变量Y的方差
,且随机变量X的分布列如图:则随机变量Y的方差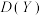 等于
等于X | 0 | 1 | 2 |
P |
|
| a |
您最近半年使用:0次
名校
解题方法
7 . 若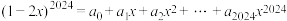 ,则
,则 ( )
( )
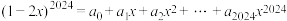 ,则
,则 ( )
( )| A.2 | B.0 | C. | D. |
您最近半年使用:0次
名校
解题方法
8 . 用0,1,2,3,4,5这两个数字可以组成多少个符合下列条件的无重复的数字?(列式并计算)
(1)六位数;
(2)六位奇数;
(3)能被5整除的六位数;
(4)组成的六位数按从小到大顺序排列,第265个数是多少?
(5)六位数中数字1,2始终相邻的数
(1)六位数;
(2)六位奇数;
(3)能被5整除的六位数;
(4)组成的六位数按从小到大顺序排列,第265个数是多少?
(5)六位数中数字1,2始终相邻的数
您最近半年使用:0次
9 . 已知0, 1, 2, 3, 4, 5这六个数字.
(1)可以组成多少个无重复数字的三位数?
(2)可以组成多少个无重复数字的三位奇数?
(3)可以组成多少个无重复数字的小于1 000的自然数?
(4)可以组成多少个无重复数字的大于3 000且小于5 421的四位数?
(1)可以组成多少个无重复数字的三位数?
(2)可以组成多少个无重复数字的三位奇数?
(3)可以组成多少个无重复数字的小于1 000的自然数?
(4)可以组成多少个无重复数字的大于3 000且小于5 421的四位数?
您最近半年使用:0次
解题方法
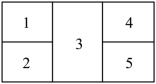
10 . 如图,现有4种不同颜色给图中5个区域涂色,要求任意两个相邻区域不同色,共有______ 种不同涂色方法;(用数字作答)
您最近半年使用:0次





