名校
1 . 若直线 :
: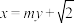 与曲线
与曲线 :
: 相交于
相交于 ,
, 两点,
两点, 为坐标原点,当
为坐标原点,当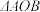 的面积取最大值时,实数
的面积取最大值时,实数 的值为( )
的值为( )
 :
: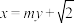 与曲线
与曲线 :
: 相交于
相交于 ,
, 两点,
两点, 为坐标原点,当
为坐标原点,当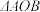 的面积取最大值时,实数
的面积取最大值时,实数 的值为( )
的值为( )A. | B.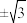 | C. | D. |
您最近半年使用:0次
名校
2 . 直线 与圆
与圆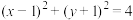 的位置关系为
的位置关系为 

 与圆
与圆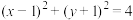 的位置关系为
的位置关系为 

| A.相离 | B.相交 | C.相切 | D.相交或相切 |
您最近半年使用:0次
3 . 把4个苹果分给两个人,每人至少一个,不同分法种数有( )
| A.6 | B.12 | C.14 | D.16 |
您最近半年使用:0次
解题方法
4 . 某学校为了丰富学生的课余生活,以班级为单位组织学生开展古诗词背诵比赛,随机抽取一首,背诵正确加10分,背诵错误减10分,且背诵结果只有“正确”和“错误”两种.其中某班级学生背诵正确的概率 ,记该班级完成
,记该班级完成 首背诵后的总得分为
首背诵后的总得分为 .
.
(1)求 且
且 的概率;
的概率;
(2)记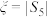 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
 ,记该班级完成
,记该班级完成 首背诵后的总得分为
首背诵后的总得分为 .
.(1)求
 且
且 的概率;
的概率;(2)记
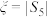 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
您最近半年使用:0次
名校
5 . 已知函数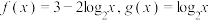 .
.
(1)当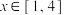 时,求函数
时,求函数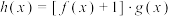 的值域;
的值域;
(2)如果对任意的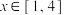 ,不等式
,不等式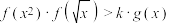 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
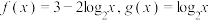 .
.(1)当
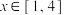 时,求函数
时,求函数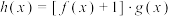 的值域;
的值域;(2)如果对任意的
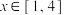 ,不等式
,不等式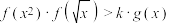 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2019-09-15更新
|
2154次组卷
|
25卷引用:重庆市第十八中学2017-2018学年高一上学期期中考试数学试题2
重庆市第十八中学2017-2018学年高一上学期期中考试数学试题2重庆市第十八中学2017-2018学年高一上学期期中考试数学试题3陕西省西安市高新第一中学国际部2017-2018学年高一上学期期中考试数学试题贵州省遵义航天高级中学2017-2018学年高二上学期期末考试数学(理)试题贵州省遵义航天高级中学2017-2018学年高二上学期期末考试数学(文)试题[市级联考】安徽省定远重点中学2019届高三上学期期中考试数学(理)试题山西省应县第一中学校2018-2019学年高二下学期期末考试数学(理)试题上海市曹杨中学2018-2019学年高一上学期期末复习卷一数学试题河北省邯郸市第一中学2019-2020学年高一上学期期中数学试题山西省大同市第一中学2019-2020学年高二下学期3月第二次考试数学(文)试题山西省大同市第一中学2019-2020学年高二下学期3月第二次考试数学(理)试题江苏省扬州市宝应县2020-2021学年高三上学期初调研测试数学试题广东省汕头市潮南区2020-2021学年高一上学期期末数学试题(已下线)专题7.2 函数综合 B卷(常考题型精选)-2021-2022学年高一数学单元卷模拟(易中难)(2019人教A版必修第一册)(已下线)专题10对数与对数函数-2022年(新高考)数学高频考点+重点题型山西省吕梁市泰化学校2020-2021学年高二下学期3月第二次考试数学(理)试题(已下线)考点15 对数函数-备战2022年高考数学一轮复习考点一遍过(新高考地区专用)【学科网名师堂】第六章 幂函数、指数函数和对数函数(选拔卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(苏教版2019必修第一册) 湖南省常德市鼎城区第一中学2021-2022学年高一上学期12月月考数学试题(已下线)第15讲 对数函数-备战2023年高考数学一轮复习考点帮(新高考专用)上海交通大学附属中学2020届高三下学期开学考试数学试题河北省定州市2022-2023学年高一上学期期末数学试题河南宋基信阳实验中学2023-2024学年高三上学期第一次月考数学试题江苏省苏州市陆慕中学2023-2024学年高一上学期12月月考数学试题(已下线)专题10 对数与对数函数
6 . 在直角坐标系 中,圆C的方程为
中,圆C的方程为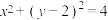 ,以
,以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线 的极坐标方程是
的极坐标方程是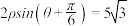 ,射 线
,射 线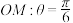 与圆C的交点为
与圆C的交点为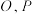 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
 中,圆C的方程为
中,圆C的方程为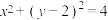 ,以
,以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.(1)求圆C的极坐标方程;
(2)直线
 的极坐标方程是
的极坐标方程是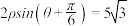 ,射 线
,射 线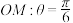 与圆C的交点为
与圆C的交点为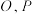 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
您最近半年使用:0次
2019-09-15更新
|
465次组卷
|
5卷引用:山西省应县第一中学校2018-2019学年高二下学期期末考试数学(理)试题
名校
7 . 把3名辅导老师与6名学生分成3个小组(每组1名教师,2名学生)开展实验活动,但学生甲必须与教师A在一起,这样的分组方法有________ 种.(用数字作答)
您最近半年使用:0次
2019-09-15更新
|
343次组卷
|
2卷引用:山西省应县第一中学校2018-2019学年高二下学期期末考试数学(理)试题
名校
8 . 设 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, 单调递减,若
单调递减,若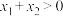 ,则
,则 的值( )
的值( )
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, 单调递减,若
单调递减,若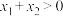 ,则
,则 的值( )
的值( )| A.恒为负值 | B.恒等于零 |
| C.恒为正值 | D.无法确定正负 |
您最近半年使用:0次
2019-09-15更新
|
667次组卷
|
9卷引用:四川省眉山市眉山中学2017-2018学年高一10月月考数学试题
四川省眉山市眉山中学2017-2018学年高一10月月考数学试题山西省应县第一中学校2018-2019学年高二下学期期末考试数学(理)试题(已下线)专题11.2 直接证明与间接证明(练)【文】-《2020年高考一轮复习讲练测》(已下线)专题12.2 直接证明与间接证明、数学归纳法(精练)-2021届高考数学(文)一轮复习讲练测(已下线)专题12.2 直接证明与间接证明 (精练)-2021届高考数学(文)一轮复习学与练(已下线)专题12.2 直接证明与间接证明、数学归纳法(精练)-2021年高考数学(理)一轮复习讲练测(已下线)专题12.2 直接证明与间接证明、数学归纳法 (精练)-2021年高考数学(理)一轮复习学与练重庆市蜀都中学2020-2021学年高二上学期11月月考数学试题甘肃省兰州市第五十中学2022-2023学年高三上学期第一次模拟考试数学(文科)试题
9 . 若直线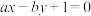 平分圆
平分圆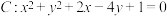 的周长,则
的周长,则 的取值范围是( )
的取值范围是( )
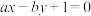 平分圆
平分圆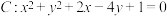 的周长,则
的周长,则 的取值范围是( )
的取值范围是( )A.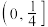 | B.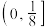 | C. | D.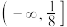 |
您最近半年使用:0次
10 . 在平行四边形 中,
中,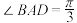 ,点
,点 在
在 边上,
边上,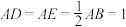 ,将
,将 沿直线
沿直线 折起成
折起成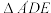 ,
, 为
为 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
 中,
中,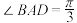 ,点
,点 在
在 边上,
边上,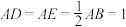 ,将
,将 沿直线
沿直线 折起成
折起成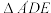 ,
, 为
为 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )A.直线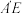 与直线 与直线 共面 共面 | B.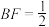 |
C.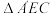 可以是直角三角形 可以是直角三角形 | D.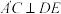 |
您最近半年使用:0次



