17. 某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 | 9.8 | 10.3 | 10.0 | 10.2 | 9.9 | 9.8 | 10.0 | 10.1 | 10.2 | 9.7 |
新设备 | 10.1 | 10.4 | 10.1 | 10.0 | 10.1 | 10.3 | 10.6 | 10.5 | 10.4 | 10.5 |
旧设备和新设备生产产品的该项指标的样本平均数分别记为

和
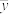
,样本方差分别记为

和

.
(1)求

,
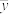
,

,

;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果
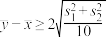
,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).