18. 2021年7月24日,中国选手杨倩在东京奥运会女子10米气步枪决赛中,为中国代表团揽入本界奥运会第一枚金牌.受奥运精神的鼓舞,某射击俱乐部组织200名射击爱好者进行一系列的测试,并记录他们的射击技能分数(单位:分),将所得数据分成7组:
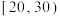
,
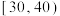
,…,
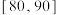
,整理得到如图所示的频率分布直方图.
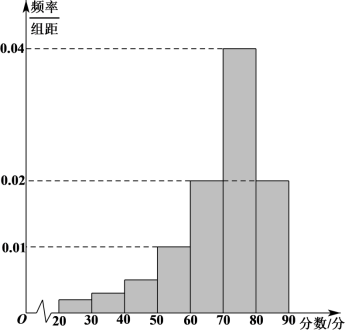
(1)求这200名射击爱好者中射击技能分数低于60分的人数;
(2)从样本中射击技能分数在
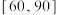
的射击爱好者中采用分层抽样的方法抽取8人,再从这8人中随机抽取3人进一步进行射击训练,记抽取的3人中射击技能分数不低于70分的人数为
X,求
X的分布列与数学期望.