19. 某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:
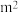
)和材积量(单位:
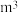
),得到如下数据:
| 样本号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
根部横截面积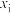 | 0.04 | 0.06 | 0.04 | 0.08 | 0.08 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.6 |
材积量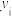 | 0.25 | 0.40 | 0.22 | 0.54 | 0.51 | 0.34 | 0.36 | 0.46 | 0.42 | 0.40 | 3.9 |
并计算得

.
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);
(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为
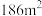
.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
附:相关系数
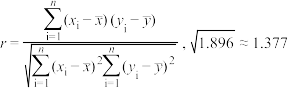
.