20. 一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如下数据:
(1)能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?
(2)从该地的人群中任选一人,
A表示事件“选到的人卫生习惯不够良好”,
B表示事件“选到的人患有该疾病”.

与
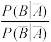
的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为
R.
(ⅰ)证明:
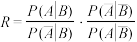
;
(ⅱ)利用该调查数据,给出
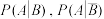
的估计值,并利用(ⅰ)的结果给出
R的估计值.
附

,

| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |