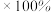18. 某校的

名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取
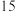
名学生的数学成绩(满分:

分),并绘制成如图所示的茎叶图.将成绩低于

分的称为“不及格”,不低于
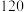
分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
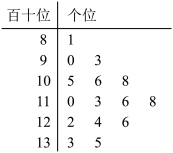
(1)估算此次联考该校高三学生的数学学科的平均成绩.
(2)估算此次联考该校高三学生数学成绩“不及格”和“优秀”的人数各是多少.
(3)在国家扶贫政策的倡导下,该地教育部门提出了教育扶贫活动,要求对此次数学成绩“不及格”的学生分两期进行学业辅导:一期由优秀学生进行一对一帮扶辅导,二期由老师进行集中辅导.根据实践总结,优秀学生进行一对一辅导的转化率为
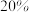
;老师集中辅导的转化率为

,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
注:转化率