22. 上饶市在某次高三适应性考试中对数学成绩数据统计显示,全市10000名学生的成绩近似服从正态分布
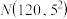
,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组
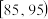
,第二组

,…,第六组

,得到如图所示的频率分布直方图:
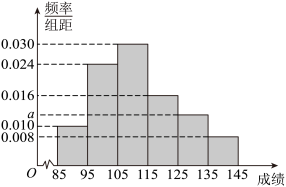
(1)试由样本频率分布直方图估计该校数学成绩的平均分数;
(2)若从这50名学生中成绩在125分(含125分)以上的同学中任意抽取3人,该3人在全市前13名的人数记为

,求

的概率.
附:若
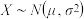
,则
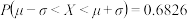
,
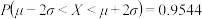
,
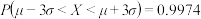
.