18. 惠州市某学校高三年级模拟考试的数学试题是全国
I卷的题型结构,其中第22,23题为选做题,考生只需从中任选一题作答.已知文科数学和理科数学的选做题题目无任何差异,该校参加模拟考试学生共
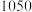
人,其中文科学生

人,理科学生

人.在测试结束后,数学老师对该学校全体高三学生选做的22题和23题得分情况进行了统计,22、23题统计结果如下表
22题得分 | 
| 
| 
| 
| 
|
理科人数 | 
| 
| 
| 
| 
|
文科人数 | 
| 
| 
| 
| 
|
23题得分 | 
| 
| 
| 
| 
|
理科人数 | 
| 
| 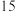
| 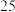
| 
|
文科人数 | 
| 
| 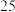
| 
| 
|
参考公式:

,其中

(1)在答卷中完成如下

列联表,并判断能否至少有

的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
(2)在第23题得分为

的学生中,按分层抽样的方法随机抽取

人进行答疑辅导,并在辅导后从这

人中随机抽取

人进行测试,求被抽中进行测试的

名学生均为理科生的概率.