已知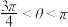 ,
,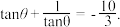
(1)求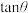 的值;
的值;
(2)求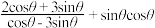 的值.
的值.
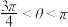 ,
,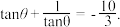
(1)求
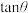 的值;
的值;(2)求
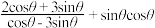 的值.
的值.
18-19高一下·广东中山·阶段练习 查看更多[4]
(已下线)5.2+三角函数的概念-2020-2021学年新教材导学导练高中数学必修第一册(人教A版)人教B版(2019) 必修第三册 过关斩将 第七章 三角函数 专题强化练2 妙用同角三角函数的基本关系求值第五章 三角函数 专题强化练6 妙用同角三角函数的基本关系求值【全国百强校】广东省中山市第一中学2018-2019学年高一下学期第一次段考(4月)数学试题
更新时间:2019-04-22 19:25:40
|
相似题推荐
解答题-证明题
|
适中
(0.65)
解题方法
【推荐1】求证:
(1)若 ,则
,则 .
.
(2)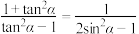 (
(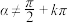 ,
,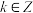 ).
).
(1)若
 ,则
,则 .
.(2)
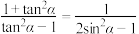 (
(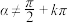 ,
,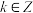 ).
).
您最近半年使用:0次
解答题-问答题
|
适中
(0.65)
解题方法
【推荐2】如图,锐角 (单位为弧度)的终边与单位圆交于点P,作
(单位为弧度)的终边与单位圆交于点P,作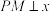 轴于点M
轴于点M

(1)利用单位圆中的三角函数线证明:当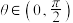 时,
时, ;
;
(2)求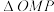 的周长与面积之和的取值范围.
的周长与面积之和的取值范围.
 (单位为弧度)的终边与单位圆交于点P,作
(单位为弧度)的终边与单位圆交于点P,作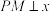 轴于点M
轴于点M
(1)利用单位圆中的三角函数线证明:当
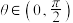 时,
时, ;
;(2)求
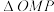 的周长与面积之和的取值范围.
的周长与面积之和的取值范围.
您最近半年使用:0次
【推荐1】已知 .
.
(1)求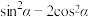 的值;
的值;
(2) 的值.
的值.
 .
.(1)求
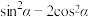 的值;
的值;(2)
 的值.
的值.
您最近半年使用:0次
解答题-问答题
|
适中
(0.65)
解题方法
【推荐2】计算:
(1)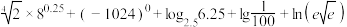
(2)已知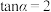 ,求
,求 值.
值.
(1)
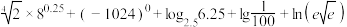
(2)已知
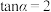 ,求
,求 值.
值.
您最近半年使用:0次

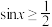 ,求:满足条件的角
,求:满足条件的角 的取值范围;
的取值范围; ,求:满足条件的角
,求:满足条件的角 .
.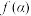 ,并求
,并求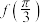 ;
;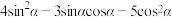 的值;
的值;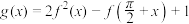 的值域.
的值域.


