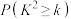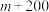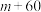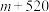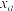1 . 为了更好地培养国家需要的人才,某校拟开展一项名为“书香致远,阅读润心”的读书活动,为了更好地服务全校学生,需要对全校学生的周平均阅读时间进行调查,现从该校学生中随机抽取200名学生,将他们的周平均阅读时间(单位:小时)数据分成5组: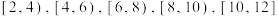 ,根据分组数据制成了如图所示的频率分布直方图.
,根据分组数据制成了如图所示的频率分布直方图. 的值,并估计全校学生周平均阅读时间的平均数;
的值,并估计全校学生周平均阅读时间的平均数;
(2)用分层抽样的方法从周平均阅读时间不小于8小时的学生中抽出6人,再随机选出2人作为该活动的形象大使,求这 人都来自
人都来自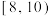 这组的概率.
这组的概率.
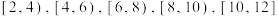 ,根据分组数据制成了如图所示的频率分布直方图.
,根据分组数据制成了如图所示的频率分布直方图.
 的值,并估计全校学生周平均阅读时间的平均数;
的值,并估计全校学生周平均阅读时间的平均数;(2)用分层抽样的方法从周平均阅读时间不小于8小时的学生中抽出6人,再随机选出2人作为该活动的形象大使,求这
 人都来自
人都来自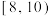 这组的概率.
这组的概率.
您最近半年使用:0次
2 . 2024年03月04日《人民日报》发表文章《开展全民健身 实现全民健康》,文中提到:体育锻炼要从小抓起.“让孩子们跑起来”“要长得壮壮的、练得棒棒的”“体育锻炼是增强少年儿童体质最有效的手段”……习近平总书记的殷殷嘱托,牢牢印刻在广大教育工作者和孩子们的心中.某学校为了了解学生体育锻炼的情况,随机抽取了n名同学,统计了他们每周体育锻炼的时间,作出了频率分布直方图如图所示.其中体育锻炼时间在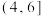 内的人数为50人.
内的人数为50人. 及
及 的值(
的值( 的取值保留三位小数);
的取值保留三位小数);
(2)估计该校学生每周体育锻炼时间的平均值(同一组中的数据用该组区间的中点值作代表);
(3)我们把每周体育锻炼时间超过8小时的学生称为“运动达人”,为了了解“运动达人”与性别是否有关系,我们对随机抽取的 名学生的性别进行了统计,得到如下
名学生的性别进行了统计,得到如下 列联表:
列联表:
补全 列联表,并判断能否有90%的把握认为成为“运动达人”与性别有关?
列联表,并判断能否有90%的把握认为成为“运动达人”与性别有关?
附:
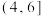 内的人数为50人.
内的人数为50人.
 及
及 的值(
的值( 的取值保留三位小数);
的取值保留三位小数);(2)估计该校学生每周体育锻炼时间的平均值(同一组中的数据用该组区间的中点值作代表);
(3)我们把每周体育锻炼时间超过8小时的学生称为“运动达人”,为了了解“运动达人”与性别是否有关系,我们对随机抽取的
 名学生的性别进行了统计,得到如下
名学生的性别进行了统计,得到如下 列联表:
列联表:非运动达人 | 运动达人 | 总计 | |
男生 | 30 | ||
女生 | 70 | ||
总计 |
 列联表,并判断能否有90%的把握认为成为“运动达人”与性别有关?
列联表,并判断能否有90%的把握认为成为“运动达人”与性别有关?附:

| 0.100 | 0.050 | 0.025 | 0.010 |
k | 2.706 | 3.841 | 5.024 | 6.635 |
您最近半年使用:0次
解题方法
3 . 继淄博烧烤、哈尔滨冻梨后,最近天水麻辣烫又火了.据了解天水麻辣烫店内菜品一般由竹签串起成捆摆放,人们按照自己的喜好选好后递给老板,进行调制.某麻辣烫店内有西兰花、香菇、豆皮、海带、白菜等菜品,一游客打算从以上5种蔬菜中随机选择不同的3种,则西兰花和海带被选中的概率为___________ .
您最近半年使用:0次
解题方法
4 . 人生因阅读而气象万千,人生因阅读而精彩纷呈.腹有诗书气自华,读书有益于开拓眼界、提升格局;最是书香能致远,书海中深蕴着灼热的理想信仰、炽热的国家情怀.对某校高中学生的读书情况进行了调查,结果如下:
附: ,其中
,其中 .
.
根据小概率值 的独立性检验,推断是否喜欢阅读与性别有关,则
的独立性检验,推断是否喜欢阅读与性别有关,则 的值可以为( )
的值可以为( )
喜欢读书 | 不喜欢读书 | 合计 | |
男生 | 260 | 60 | 320 |
女生 | 200 | m |
|
合计 | 460 |
|
|
 ,其中
,其中 .
.
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 的独立性检验,推断是否喜欢阅读与性别有关,则
的独立性检验,推断是否喜欢阅读与性别有关,则 的值可以为( )
的值可以为( )| A.10 | B.20 | C.30 | D.40 |
您最近半年使用:0次
名校
解题方法
5 . 从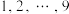 这九个数字中任取两个,这两个数的和为质数的概率为( )
这九个数字中任取两个,这两个数的和为质数的概率为( )
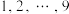 这九个数字中任取两个,这两个数的和为质数的概率为( )
这九个数字中任取两个,这两个数的和为质数的概率为( )A. | B.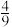 | C. | D.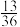 |
您最近半年使用:0次
今日更新
|
729次组卷
|
3卷引用:陕西省铜川市2024届高三第二次质量检测数学(文科)试题
6 . 2024年03月04日《人民日报》发表文章《开展全民健身实现全民健康》,文中提到:体育锻炼要从小抓起.“让孩子们跑起来”“要长得壮壮的、练得棒棒的”“体育锻炼是增强少年儿童体质最有效的手段”…….习近平总书记的殷殷嘱托,牢牢印刻在广大教育工作者和孩子们的心中.某学校为了了解学生体育锻炼的情况,随机抽取了n名同学,统计了他们每周体育锻炼的时间,作出了频率分布直方图如图所示.其中体育锻炼时间在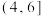 内的人数为50人.
内的人数为50人.
(2)试估计该校学生每周体育锻炼时间的平均值(同一组数据用该区间的中点值作代表);
(3)以频率估计概率,在该校学生中任取4人,设X为这4人中每周体育锻炼时间在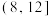 内的人数,求X的分布列及数学期望.
内的人数,求X的分布列及数学期望.
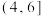 内的人数为50人.
内的人数为50人.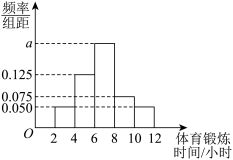
(2)试估计该校学生每周体育锻炼时间的平均值(同一组数据用该区间的中点值作代表);
(3)以频率估计概率,在该校学生中任取4人,设X为这4人中每周体育锻炼时间在
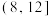 内的人数,求X的分布列及数学期望.
内的人数,求X的分布列及数学期望.
您最近半年使用:0次
解题方法
7 . 通常人们认为语文作文成绩与课外阅读习惯(阅读习惯分为良好和不够良好两类)有很大关联,为了研究这个看法是否可信,某课外研究小组从学校一次期中测试语文作文成绩优秀的学生中随机调查了200人,同时在语文作文成绩不够优秀的学生中也随机调查了200人,得到如下数据:
(1)在这400名学生中按照课外阅读习惯良好与否进行分层随机抽样,抽取20名学生了解学生的行为习惯形成的原因,再从这20名学生中任选3人进行面对面访谈,求这3名学生中至少有1人课外阅读习惯良好的概率;
(2)根据小概率值 的独立性检验,能否认为语文作文成绩与课外阅读习惯有关联?
的独立性检验,能否认为语文作文成绩与课外阅读习惯有关联?
附: .
.
| 语文作文成绩 | 课外阅读习惯 | 合计 | |
| 不够良好 | 良好 | ||
| 优秀 | 60 | 140 | 200 |
| 不够优秀 | 180 | 20 | 200 |
| 合计 | 240 | 160 | 400 |
(2)根据小概率值
 的独立性检验,能否认为语文作文成绩与课外阅读习惯有关联?
的独立性检验,能否认为语文作文成绩与课外阅读习惯有关联?附:
 .
.
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
解题方法
8 . 投壶是中国古代士大夫宴饮时做的一种投掷游戏,游戏方式是把箭向壶里投.《醉翁亭记》中的“射”指的就是“投壶”这个游戏.为弘扬传统文化,某单位开展投壶游戏,现甲、乙两人为一组玩投壶游戏,每次由其中一人投壶,规则如下:若投中,则此人继续投壶,若未投中,则换为对方投壶,无论之前投壶的情况如何,甲每次投壶的命中率均为 ,乙每次投壶的命中率均为
,乙每次投壶的命中率均为 ,由抽签确定第1次投壶的人选,第1次投壶的人是甲、乙的概率各为
,由抽签确定第1次投壶的人选,第1次投壶的人是甲、乙的概率各为 .第3次投壶的人是乙的概率为
.第3次投壶的人是乙的概率为_______ ,已知在第2次投壶的人是甲的情况下,第1次投壶的人是乙的概率为_______ .
 ,乙每次投壶的命中率均为
,乙每次投壶的命中率均为 ,由抽签确定第1次投壶的人选,第1次投壶的人是甲、乙的概率各为
,由抽签确定第1次投壶的人选,第1次投壶的人是甲、乙的概率各为 .第3次投壶的人是乙的概率为
.第3次投壶的人是乙的概率为
您最近半年使用:0次
2024高二下·江苏·专题练习
解题方法
9 . 在一段时间内,分5次测得某种商品的价格x(万元)和需求量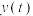 之间的一组数据为
之间的一组数据为
已知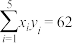 ,
, .
.
(1)画出散点图;
(2)求出y关于x的线性回归方程;
(3)如果价格定为1.9万元,预测需求量大约是多少?
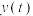 之间的一组数据为
之间的一组数据为| 1 | 2 | 3 | 4 | 5 | |
价格 | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
| 需求量y | 12 | 10 | 7 | 5 | 3 |
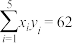 ,
, .
.(1)画出散点图;
(2)求出y关于x的线性回归方程;
(3)如果价格定为1.9万元,预测需求量大约是多少?
您最近半年使用:0次
解题方法
10 . 在某公司举办的职业技能竞赛中,只有甲、乙两人晋级决赛,已知决赛第一天采用五场三胜制,即先赢三场者获胜,当天的比赛结束,决赛第二天的赛制与第一天相同.在两天的比赛中,若某位选手连胜两天,则他获得最终冠军,决赛结束,若两位选手各胜一天,则需进行第三天的比赛,第三天的比赛为三场两胜制,即先赢两场者获胜,并获得最终冠军,决赛结束.每天每场的比赛只有甲胜与乙胜两种结果,每场比赛的结果相互独立,且每场比赛甲获胜的概率均为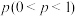 .
.
(1)若 ,求第一天比赛的总场数为4的概率;
,求第一天比赛的总场数为4的概率;
(2)若 ,求决出最终冠军时比赛的总场数至多为8的概率.
,求决出最终冠军时比赛的总场数至多为8的概率.
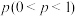 .
.(1)若
 ,求第一天比赛的总场数为4的概率;
,求第一天比赛的总场数为4的概率;(2)若
 ,求决出最终冠军时比赛的总场数至多为8的概率.
,求决出最终冠军时比赛的总场数至多为8的概率.
您最近半年使用:0次
昨日更新
|
738次组卷
|
3卷引用:河南省濮阳市2024届高三下学期(开学)第一次模拟考试数学试题