解题方法
1 . 在棱长为 的正方体
的正方体 中,
中, ,
, ,
, 分别为棱
分别为棱 ,
, ,
, 的中点,动点
的中点,动点 在平面
在平面 内,且
内,且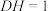 .则下列说法正确的是( )
.则下列说法正确的是( )
 的正方体
的正方体 中,
中, ,
, ,
, 分别为棱
分别为棱 ,
, ,
, 的中点,动点
的中点,动点 在平面
在平面 内,且
内,且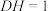 .则下列说法正确的是( )
.则下列说法正确的是( )
A.存在点 ,使得直线 ,使得直线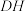 与直线 与直线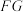 相交 相交 |
B.存在点 ,使得直线 ,使得直线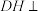 平面 平面 |
C.直线 与平面 与平面 所成角的大小为 所成角的大小为 |
D.平面 被正方体所截得的截面面积为 被正方体所截得的截面面积为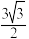 |
您最近半年使用:0次
2 . 如图, 是边长为2的正方形,
是边长为2的正方形, ,
,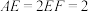 ,
,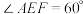 ,
, .
. ;
;
(2)求平面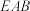 与平面
与平面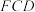 夹角的余弦值.
夹角的余弦值.
 是边长为2的正方形,
是边长为2的正方形, ,
,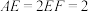 ,
,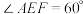 ,
, .
.
 ;
;(2)求平面
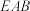 与平面
与平面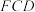 夹角的余弦值.
夹角的余弦值.
您最近半年使用:0次
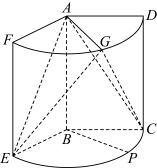
3 . 如图,几何体是圆柱的一部分,它是由矩形 (及其内部)以
(及其内部)以 边所在直线为旋转轴旋转
边所在直线为旋转轴旋转 得到的,点
得到的,点 是
是 的中点,点
的中点,点 在
在 上,异面直线
上,异面直线 与
与 所成的角是
所成的角是 .
. ;
;
(2)若 ,
,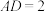 ,求二面角
,求二面角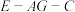 的大小.
的大小.
 (及其内部)以
(及其内部)以 边所在直线为旋转轴旋转
边所在直线为旋转轴旋转 得到的,点
得到的,点 是
是 的中点,点
的中点,点 在
在 上,异面直线
上,异面直线 与
与 所成的角是
所成的角是 .
.
 ;
;(2)若
 ,
,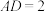 ,求二面角
,求二面角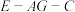 的大小.
的大小.
您最近半年使用:0次
4 . 在菱形 中,
中,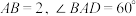 ,以
,以 为轴将菱形
为轴将菱形 翻折到菱形
翻折到菱形 ,使得平面
,使得平面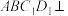 平面
平面 ,点
,点 为边
为边 的中点,连接
的中点,连接 .
.
 平面
平面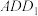 ;
;
(2)求直线 与平面
与平面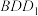 所成角的正弦值.
所成角的正弦值.
 中,
中,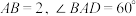 ,以
,以 为轴将菱形
为轴将菱形 翻折到菱形
翻折到菱形 ,使得平面
,使得平面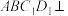 平面
平面 ,点
,点 为边
为边 的中点,连接
的中点,连接 .
.

 平面
平面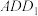 ;
;(2)求直线
 与平面
与平面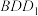 所成角的正弦值.
所成角的正弦值.
您最近半年使用:0次
解题方法
5 . 如图,圆柱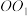 内有一个直三棱柱
内有一个直三棱柱 ,三棱柱的底面三角形内接于圆柱底面,已知圆柱
,三棱柱的底面三角形内接于圆柱底面,已知圆柱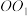 的轴截面是边长为6的正方形,
的轴截面是边长为6的正方形, ,点
,点 在线段
在线段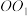 上运动.
上运动.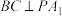 ;
;
(2)当 时,求
时,求 与平面
与平面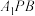 所成角的正弦值.
所成角的正弦值.
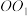 内有一个直三棱柱
内有一个直三棱柱 ,三棱柱的底面三角形内接于圆柱底面,已知圆柱
,三棱柱的底面三角形内接于圆柱底面,已知圆柱 的轴截面是边长为6的正方形,
的轴截面是边长为6的正方形, ,点
,点 在线段
在线段 上运动.
上运动.
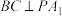 ;
;(2)当
 时,求
时,求 与平面
与平面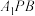 所成角的正弦值.
所成角的正弦值.
您最近半年使用:0次
名校
6 . 如图,在四棱锥 中,四边形
中,四边形 为梯形,其中
为梯形,其中 ,
,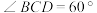 ,
,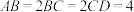 ,平面
,平面 平面
平面 .
.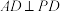 ;
;
(2)若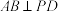 ,且
,且 与平面
与平面 所成角的正切值为2,求平面
所成角的正切值为2,求平面 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
 中,四边形
中,四边形 为梯形,其中
为梯形,其中 ,
,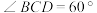 ,
,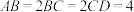 ,平面
,平面 平面
平面 .
.
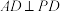 ;
;(2)若
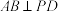 ,且
,且 与平面
与平面 所成角的正切值为2,求平面
所成角的正切值为2,求平面 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
您最近半年使用:0次
名校
7 . 四棱锥 中,四边形ABCD为菱形,
中,四边形ABCD为菱形, ,平面
,平面 平面ABCD.
平面ABCD. ;
;
(2)若 ,且PA与平面ABCD成角为
,且PA与平面ABCD成角为 ,点E在棱PC上,且
,点E在棱PC上,且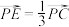 ,求平面EBD与平面BCD的夹角的余弦值.
,求平面EBD与平面BCD的夹角的余弦值.
 中,四边形ABCD为菱形,
中,四边形ABCD为菱形, ,平面
,平面 平面ABCD.
平面ABCD.
 ;
;(2)若
 ,且PA与平面ABCD成角为
,且PA与平面ABCD成角为 ,点E在棱PC上,且
,点E在棱PC上,且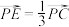 ,求平面EBD与平面BCD的夹角的余弦值.
,求平面EBD与平面BCD的夹角的余弦值.
您最近半年使用:0次
今日更新
|
368次组卷
|
6卷引用:海南省琼海市嘉积中学2022-2023学年高二上学期期末数学试题
海南省琼海市嘉积中学2022-2023学年高二上学期期末数学试题云南省开远市第一中学校2023-2024学年高二上学期10月月考数学试题(已下线)第02讲:空间向量与立体几何交汇(必刷6大考题+7大题型)-2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019选择性必修第一册)河南省周口市川汇区周口恒大中学2023-2024学年高二上学期期末数学试题江苏省南通市新高考2024届高三适应性测试数学模拟试题海南省文昌中学2023-2024学年高二下学期第一次月考数学试题
解题方法
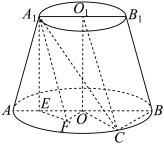
8 . 如图,在圆台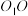 中,
中,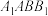 为轴截面,
为轴截面, 为下底面圆周上一点,
为下底面圆周上一点, 为下底面圆
为下底面圆 内一点,
内一点,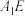 垂直下底面圆
垂直下底面圆 于点
于点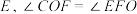 .
.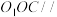 平面
平面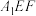 ;
;
(2)若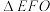 为等边三角形,求平面
为等边三角形,求平面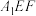 和平面
和平面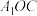 的交线
的交线 与平面
与平面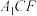 所成角的正弦值.
所成角的正弦值.
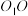 中,
中,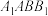 为轴截面,
为轴截面, 为下底面圆周上一点,
为下底面圆周上一点, 为下底面圆
为下底面圆 内一点,
内一点,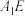 垂直下底面圆
垂直下底面圆 于点
于点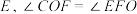 .
.
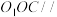 平面
平面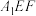 ;
;(2)若
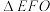 为等边三角形,求平面
为等边三角形,求平面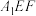 和平面
和平面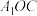 的交线
的交线 与平面
与平面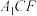 所成角的正弦值.
所成角的正弦值.
您最近半年使用:0次
2024·全国·模拟预测
解题方法
9 . 图(1)为梯形 ,
,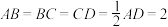 ,
, 为
为 的中点.将梯形
的中点.将梯形 沿
沿 折起,使点
折起,使点 在平面
在平面 内的射影为
内的射影为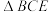 的重心
的重心 ,如图(2).
,如图(2).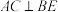 .
.
(2)若 为
为 的中点,求
的中点,求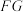 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 ,
, ,
, 为
为 的中点.将梯形
的中点.将梯形 沿
沿 折起,使点
折起,使点 在平面
在平面 内的射影为
内的射影为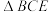 的重心
的重心 ,如图(2).
,如图(2).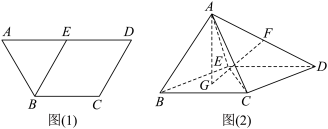
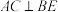 .
.(2)若
 为
为 的中点,求
的中点,求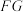 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近半年使用:0次
解题方法
10 . 如图,在底面为等边三角形的直三棱柱 中,
中,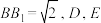 分别为棱
分别为棱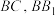 的中点,
的中点, 为棱
为棱 上的动点,且线段
上的动点,且线段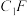 的长度最小值为
的长度最小值为 ,则异面直线
,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )
 中,
中,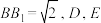 分别为棱
分别为棱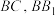 的中点,
的中点, 为棱
为棱 上的动点,且线段
上的动点,且线段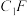 的长度最小值为
的长度最小值为 ,则异面直线
,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )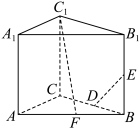
A.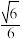 | B. | C.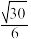 | D. |
您最近半年使用:0次



