解题方法
1 . 在棱雉 中,
中, 平面
平面 .四边形
.四边形 为平行四边形.
为平行四边形.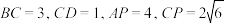 .
.
(1)求证: 平面
平面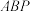 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
 中,
中, 平面
平面 .四边形
.四边形 为平行四边形.
为平行四边形.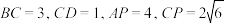 .
.
(1)求证:
 平面
平面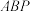 ;
;(2)求点
 到平面
到平面 的距离.
的距离.
您最近半年使用:0次
2 . 如图,在三棱锥 中,
中, 底面
底面 ,
,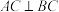 ,
, 为
为 的中点,
的中点, 为
为 的中点,
的中点,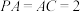 ,
, .
.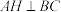 ;
;
(2)求点 到平面
到平面 的距离;
的距离;
(3)在线段 上是否存在点
上是否存在点 ,使
,使
 平面
平面 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
 中,
中, 底面
底面 ,
,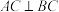 ,
, 为
为 的中点,
的中点, 为
为 的中点,
的中点,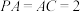 ,
, .
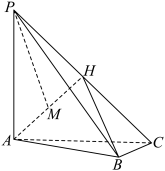
.
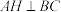 ;
;(2)求点
 到平面
到平面 的距离;
的距离;(3)在线段
 上是否存在点
上是否存在点 ,使
,使
 平面
平面 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
您最近半年使用:0次
名校
解题方法
3 . 如图,四棱锥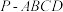 的底面是矩形,
的底面是矩形, 平面
平面 ,
, 为
为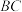 的中点,且
的中点,且 ,
,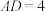 ,
,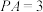 .
. 到平面
到平面 的距离;
的距离;
(2)求二面角 的余弦值.
的余弦值.
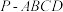 的底面是矩形,
的底面是矩形, 平面
平面 ,
, 为
为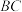 的中点,且
的中点,且 ,
,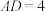 ,
,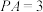 .
.
 到平面
到平面 的距离;
的距离;(2)求二面角
 的余弦值.
的余弦值.
您最近半年使用:0次
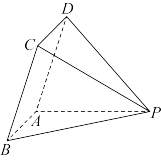
4 . 如图,在四面体 中,
中, ,
, ,
, 两两垂直,已知
两两垂直,已知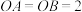 ,
,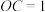 ,则点O到平面
,则点O到平面 的距离为( )
的距离为( )
 中,
中, ,
, ,
, 两两垂直,已知
两两垂直,已知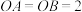 ,
,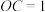 ,则点O到平面
,则点O到平面 的距离为( )
的距离为( )
A.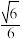 | B. | C. | D. |
您最近半年使用:0次
5 . 如图,在四棱锥 中,底面四边形
中,底面四边形 为矩形,
为矩形, ,
, ,
, ,
,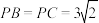 ,
, 平面
平面 ;
;
(2)若点 为
为 的中点,求三棱锥
的中点,求三棱锥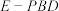 的体积.
的体积.
 中,底面四边形
中,底面四边形 为矩形,
为矩形, ,
, ,
, ,
,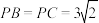 ,
,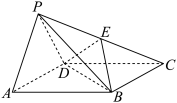
 平面
平面 ;
;(2)若点
 为
为 的中点,求三棱锥
的中点,求三棱锥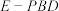 的体积.
的体积.
您最近半年使用:0次
6 . 如图,四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形,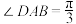 ,侧面
,侧面 是边长为4的正三角形,
是边长为4的正三角形,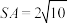 .
. 平面ABCD;
平面ABCD;
(2)求点A到平面SBC的距离.
 中,底面ABCD为菱形,
中,底面ABCD为菱形,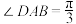 ,侧面
,侧面 是边长为4的正三角形,
是边长为4的正三角形,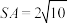 .
.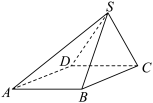
 平面ABCD;
平面ABCD;(2)求点A到平面SBC的距离.
您最近半年使用:0次
解题方法
7 . 在棱长为1的正方体 中,过面对角线
中,过面对角线 的平面记为
的平面记为 ,以下四个命题:
,以下四个命题: ,使
,使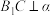 ;
;
②若平面 与平面
与平面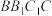 的交线为
的交线为 ,则存在直线
,则存在直线 ,使
,使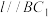 ;
;
③若平面 截正方体所得的截面为三角形,则该截面三角形面积的最大值为
截正方体所得的截面为三角形,则该截面三角形面积的最大值为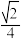 ;
;
④若平面 过点
过点 ,点
,点 在线段
在线段 上运动,则点
上运动,则点 到平面
到平面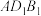 的距离为
的距离为 .
.
其中真命题的序号为____________ .
 中,过面对角线
中,过面对角线 的平面记为
的平面记为 ,以下四个命题:
,以下四个命题:
 ,使
,使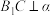 ;
;②若平面
 与平面
与平面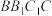 的交线为
的交线为 ,则存在直线
,则存在直线 ,使
,使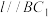 ;
;③若平面
 截正方体所得的截面为三角形,则该截面三角形面积的最大值为
截正方体所得的截面为三角形,则该截面三角形面积的最大值为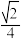 ;
;④若平面
 过点
过点 ,点
,点 在线段
在线段 上运动,则点
上运动,则点 到平面
到平面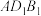 的距离为
的距离为 .
.其中真命题的序号为
您最近半年使用:0次
2024高三·上海·专题练习
解题方法
8 . 如图,在四棱锥 中,
中, 平面
平面 ,
, ,
, ,
,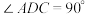 ,
, 分别为
分别为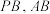 的中点.
的中点. 平面
平面 ;
;
(2)求点 到平面
到平面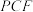 的距离.
的距离.
 中,
中, 平面
平面 ,
, ,
, ,
,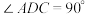 ,
, 分别为
分别为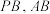 的中点.
的中点.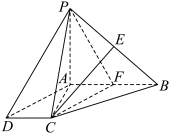
 平面
平面 ;
;(2)求点
 到平面
到平面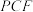 的距离.
的距离.
您最近半年使用:0次
9 . 在四棱锥 中,
中,

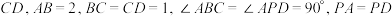 ,平面
,平面 平面
平面 .
. 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
 中,
中,

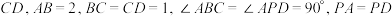 ,平面
,平面 平面
平面 .
.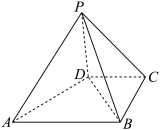
 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离.
您最近半年使用:0次

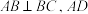 ∥
∥ ,且
,且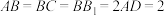 .
.
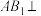 平面
平面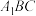 ;
;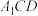 的距离.
的距离.


