名校
1 . 已知函数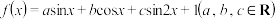 .
.
(1)当 时,求
时,求 的值域;
的值域;
(2)当 时,设
时,设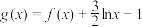 ,求证:函数
,求证:函数 有且只有一个零点;
有且只有一个零点;
(3)当 时,若实数
时,若实数 使得
使得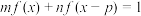 对任意实数
对任意实数 恒成立,求
恒成立,求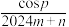 的值.
的值.
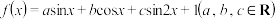 .
.(1)当
 时,求
时,求 的值域;
的值域;(2)当
 时,设
时,设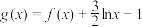 ,求证:函数
,求证:函数 有且只有一个零点;
有且只有一个零点;(3)当
 时,若实数
时,若实数 使得
使得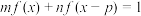 对任意实数
对任意实数 恒成立,求
恒成立,求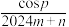 的值.
的值.
您最近半年使用:0次
名校
解题方法
2 . 已知 为常数,函数
为常数,函数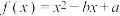 .
.
(1)当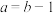 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;
(2)当 时,若函数
时,若函数 在
在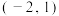 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;
(3)对于给定的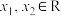 ,且
,且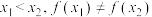 ,证明:关于
,证明:关于 的方程
的方程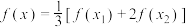 在区间
在区间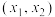 内有一个实数根.
内有一个实数根.
 为常数,函数
为常数,函数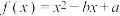 .
.(1)当
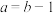 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;(2)当
 时,若函数
时,若函数 在
在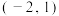 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;(3)对于给定的
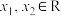 ,且
,且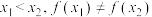 ,证明:关于
,证明:关于 的方程
的方程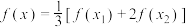 在区间
在区间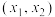 内有一个实数根.
内有一个实数根.
您最近半年使用:0次
名校
3 . 已知函数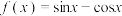
(1)求方程 在
在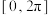 上的解集
上的解集
(2)设函数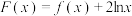 ,
,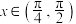 .
.
①证明: 在区间
在区间 上有且只有一个零点;
上有且只有一个零点;
②记函数 的零点为
的零点为 ,证明:
,证明: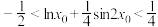
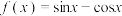
(1)求方程
 在
在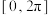 上的解集
上的解集(2)设函数
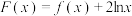 ,
,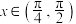 .
.①证明:
 在区间
在区间 上有且只有一个零点;
上有且只有一个零点;②记函数
 的零点为
的零点为 ,证明:
,证明: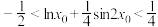
您最近半年使用:0次
2024高三·全国·专题练习
解题方法
4 . 函数f(x)=2x+x-2的零点个数是( )
| A.0 | B.1 |
| C.2 | D.3 |
您最近半年使用:0次
名校
解题方法
5 . 已知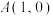 ,点
,点 在曲线
在曲线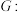
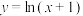 上,若线段
上,若线段 与曲线
与曲线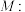
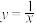 相交且交点恰为线段
相交且交点恰为线段 的中点,则称
的中点,则称 为曲线
为曲线 关于曲线
关于曲线 的一个关联点.记曲线
的一个关联点.记曲线 关于曲线
关于曲线 的关联点的个数为a,则( )
的关联点的个数为a,则( )
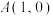 ,点
,点 在曲线
在曲线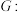
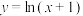 上,若线段
上,若线段 与曲线
与曲线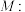
 相交且交点恰为线段
相交且交点恰为线段 的中点,则称
的中点,则称 为曲线
为曲线 关于曲线
关于曲线 的一个关联点.记曲线
的一个关联点.记曲线 关于曲线
关于曲线 的关联点的个数为a,则( )
的关联点的个数为a,则( )A. | B. | C. | D. |
您最近半年使用:0次
名校
解题方法
6 . 设函数 .
.
(1)求函数 在
在 上的单调区间;
上的单调区间;
(2)求证:函数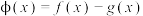 在
在 上有且只有一个零点
上有且只有一个零点 ,并求
,并求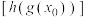 (
( 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ).
).
参考数据: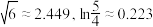 .
.
 .
.(1)求函数
 在
在 上的单调区间;
上的单调区间;(2)求证:函数
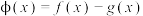 在
在 上有且只有一个零点
上有且只有一个零点 ,并求
,并求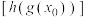 (
( 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ).
).参考数据:
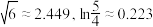 .
.
您最近半年使用:0次
7 . 已知函数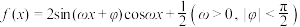 的图象关于直线
的图象关于直线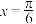 对称,其最小正周期与函数
对称,其最小正周期与函数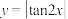 相同.
相同.
(1)求 的单调递减区间;
的单调递减区间;
(2)设函数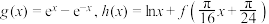 ,证明:
,证明: 有且只有一个零点
有且只有一个零点 ,且
,且 .
.
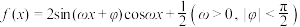 的图象关于直线
的图象关于直线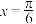 对称,其最小正周期与函数
对称,其最小正周期与函数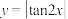 相同.
相同.(1)求
 的单调递减区间;
的单调递减区间;(2)设函数
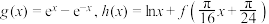 ,证明:
,证明: 有且只有一个零点
有且只有一个零点 ,且
,且 .
.
您最近半年使用:0次
解题方法
8 . 定义:如果函数 在
在 上存在
上存在 (
( ),满足
),满足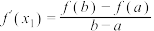 ,
,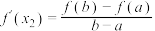 ,则称函数
,则称函数 是
是 上的“双中值函数”.已知函数
上的“双中值函数”.已知函数 是
是 上的“双中值函数”,则实数a的取值范围是
上的“双中值函数”,则实数a的取值范围是______ .
 在
在 上存在
上存在 (
( ),满足
),满足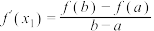 ,
,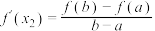 ,则称函数
,则称函数 是
是 上的“双中值函数”.已知函数
上的“双中值函数”.已知函数 是
是 上的“双中值函数”,则实数a的取值范围是
上的“双中值函数”,则实数a的取值范围是
您最近半年使用:0次
9 . 函数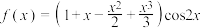 在区间
在区间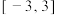 上的零点个数有
上的零点个数有______ 个.
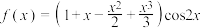 在区间
在区间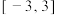 上的零点个数有
上的零点个数有
您最近半年使用:0次
10 . 已知函数

(1)当 时,若
时,若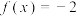 ,求x的值:
,求x的值:
(2)若 是偶函数,求出m的值:
是偶函数,求出m的值:
(3) 时,讨论方程
时,讨论方程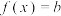 根的个数.并说明理由.
根的个数.并说明理由.


(1)当
 时,若
时,若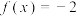 ,求x的值:
,求x的值:(2)若
 是偶函数,求出m的值:
是偶函数,求出m的值:(3)
 时,讨论方程
时,讨论方程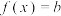 根的个数.并说明理由.
根的个数.并说明理由.
您最近半年使用:0次



