2024·全国·模拟预测
1 . 已知函数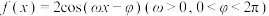 的部分图象如图,则关于
的部分图象如图,则关于 的不等式
的不等式 的解集是
的解集是______ .
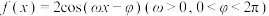 的部分图象如图,则关于
的部分图象如图,则关于 的不等式
的不等式 的解集是
的解集是
您最近半年使用:0次
名校
2 . 函数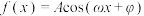 (
( ,
, ,
,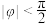 )的部分图像如图所示.
)的部分图像如图所示. 的解析式;
的解析式;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)将函数 的图像上的各点的纵坐标保持不变,横坐标伸长为原来的2倍,得到函数
的图像上的各点的纵坐标保持不变,横坐标伸长为原来的2倍,得到函数 的图像,若
的图像,若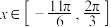 时,
时, 的图像与直线
的图像与直线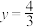 恰有三个公共点,记三个公共点的横坐标分别为
恰有三个公共点,记三个公共点的横坐标分别为 ,
, ,
, 且
且 ,求
,求 的值.
的值.
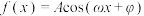 (
( ,
, ,
,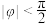 )的部分图像如图所示.
)的部分图像如图所示.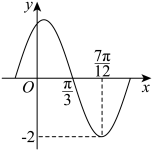
 的解析式;
的解析式;(2)求函数
 的单调递增区间;
的单调递增区间;(3)将函数
 的图像上的各点的纵坐标保持不变,横坐标伸长为原来的2倍,得到函数
的图像上的各点的纵坐标保持不变,横坐标伸长为原来的2倍,得到函数 的图像,若
的图像,若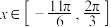 时,
时, 的图像与直线
的图像与直线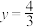 恰有三个公共点,记三个公共点的横坐标分别为
恰有三个公共点,记三个公共点的横坐标分别为 ,
, ,
, 且
且 ,求
,求 的值.
的值.
您最近半年使用:0次
7日内更新
|
487次组卷
|
5卷引用:湖北省云学名校联盟2023-2024学年高一下学期3月联考数学试卷
3 . 已知函数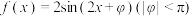 ,将函数
,将函数 向右平移
向右平移 个单位得到的图像关于
个单位得到的图像关于 轴对称且当
轴对称且当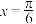 时,
时, 取得最大值.
取得最大值.
(1)求函数 的解析式:
的解析式:
(2)将函数 图象上所有的点向右平移
图象上所有的点向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若
的图象,若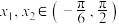 ,且
,且 ,求
,求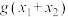 的值.
的值.
(3)方程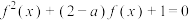 在
在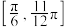 上有4个不相等的实数根,求实数
上有4个不相等的实数根,求实数 的取值范围.
的取值范围.
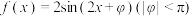 ,将函数
,将函数 向右平移
向右平移 个单位得到的图像关于
个单位得到的图像关于 轴对称且当
轴对称且当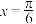 时,
时, 取得最大值.
取得最大值.(1)求函数
 的解析式:
的解析式:(2)将函数
 图象上所有的点向右平移
图象上所有的点向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若
的图象,若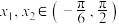 ,且
,且 ,求
,求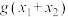 的值.
的值.(3)方程
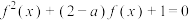 在
在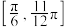 上有4个不相等的实数根,求实数
上有4个不相等的实数根,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
名校
解题方法
4 . 已知函数 ,将函数
,将函数 的图象上的点纵坐标不变,横坐标变为原来的
的图象上的点纵坐标不变,横坐标变为原来的 倍,再向右平移
倍,再向右平移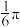 个单位长度,得到函数
个单位长度,得到函数 的图象.
的图象.
(1)写出函数 的解析式;
的解析式;
(2)试判断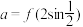 ,
,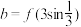 ,
,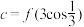 的大小;
的大小;
(3)如果函数 的定义域为
的定义域为 ,若对于任意
,若对于任意 ,
,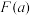 ,
,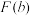 ,
, 分别为某个三角形的边长,则称
分别为某个三角形的边长,则称 为“三角形函数”.记
为“三角形函数”.记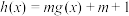 ,当定义域为
,当定义域为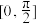 时,
时, 为“三角形函数”,求实数
为“三角形函数”,求实数 的取值范围.
的取值范围.
 ,将函数
,将函数 的图象上的点纵坐标不变,横坐标变为原来的
的图象上的点纵坐标不变,横坐标变为原来的 倍,再向右平移
倍,再向右平移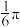 个单位长度,得到函数
个单位长度,得到函数 的图象.
的图象.(1)写出函数
 的解析式;
的解析式;(2)试判断
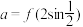 ,
,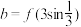 ,
,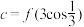 的大小;
的大小;(3)如果函数
 的定义域为
的定义域为 ,若对于任意
,若对于任意 ,
,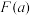 ,
,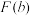 ,
, 分别为某个三角形的边长,则称
分别为某个三角形的边长,则称 为“三角形函数”.记
为“三角形函数”.记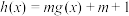 ,当定义域为
,当定义域为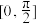 时,
时, 为“三角形函数”,求实数
为“三角形函数”,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
5 . 已知函数 ,把函数
,把函数 的图像先向右平移
的图像先向右平移 个单位长度,再向下平移
个单位长度,再向下平移 个单位,得到函数
个单位,得到函数 的图像.
的图像.
(1)求 的单调递增区间及对称轴方程;
的单调递增区间及对称轴方程;
(2)当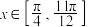 时,若方程
时,若方程 恰好有两个不同的根
恰好有两个不同的根 ,求
,求 的取值范围及
的取值范围及 的值.
的值.
 ,把函数
,把函数 的图像先向右平移
的图像先向右平移 个单位长度,再向下平移
个单位长度,再向下平移 个单位,得到函数
个单位,得到函数 的图像.
的图像.(1)求
 的单调递增区间及对称轴方程;
的单调递增区间及对称轴方程;(2)当
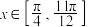 时,若方程
时,若方程 恰好有两个不同的根
恰好有两个不同的根 ,求
,求 的取值范围及
的取值范围及 的值.
的值.
您最近半年使用:0次
2024-04-07更新
|
368次组卷
|
2卷引用:重庆市杨家坪中学2023-2024学年高一下学期3月月考数学试卷
6 . 已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)将函数 的图象向右平移
的图象向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若关于
的图象,若关于 的方程
的方程 在
在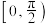 上恰有一解,求实数
上恰有一解,求实数 的取值范围.
的取值范围.
 .
.(1)求函数
 的最小正周期;
的最小正周期;(2)将函数
 的图象向右平移
的图象向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若关于
的图象,若关于 的方程
的方程 在
在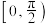 上恰有一解,求实数
上恰有一解,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
名校
解题方法
7 . 已知函数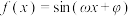 (
( ,
,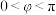 )的最小正周期为
)的最小正周期为 ,图象的一个对称中心为
,图象的一个对称中心为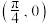 ,将函数
,将函数 图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移
图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移 个单位长度后得到函数
个单位长度后得到函数 的图象.
的图象.
(1)求函数 与
与 的解析式;
的解析式;
(2)求实数 与正整数
与正整数 ,使得
,使得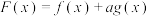 在
在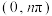 内恰有2013个零点.
内恰有2013个零点.
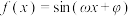 (
( ,
,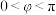 )的最小正周期为
)的最小正周期为 ,图象的一个对称中心为
,图象的一个对称中心为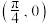 ,将函数
,将函数 图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移
图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移 个单位长度后得到函数
个单位长度后得到函数 的图象.
的图象.(1)求函数
 与
与 的解析式;
的解析式;(2)求实数
 与正整数
与正整数 ,使得
,使得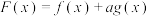 在
在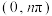 内恰有2013个零点.
内恰有2013个零点.
您最近半年使用:0次
8 . 已知函数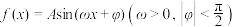 .
.
(1)某同学打算用“五点法”画出函数 再某一周期内的图象,列表如下:
再某一周期内的图象,列表如下:
请填写上表的空格处,并写出函数 的解析式;
的解析式;
(2)若函数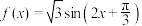 ,将
,将 图象上各点的纵坐标不变、横坐标扩大到原来的2倍,再向右平移
图象上各点的纵坐标不变、横坐标扩大到原来的2倍,再向右平移 个单位,得到函数
个单位,得到函数 的图象,若
的图象,若 在
在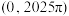 上恰有奇数个零点,求实数a与零点的个数.
上恰有奇数个零点,求实数a与零点的个数.
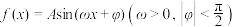 .
.(1)某同学打算用“五点法”画出函数
 再某一周期内的图象,列表如下:
再某一周期内的图象,列表如下:| x | 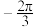 |  | 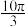 | ||
 | 0 |  |  | 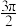 |  |
 | 0 | 1 | 0 |  | 0 |
 | 0 |  | 0 | 0 |
 的解析式;
的解析式;(2)若函数
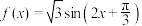 ,将
,将 图象上各点的纵坐标不变、横坐标扩大到原来的2倍,再向右平移
图象上各点的纵坐标不变、横坐标扩大到原来的2倍,再向右平移 个单位,得到函数
个单位,得到函数 的图象,若
的图象,若 在
在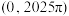 上恰有奇数个零点,求实数a与零点的个数.
上恰有奇数个零点,求实数a与零点的个数.
您最近半年使用:0次
解题方法
9 . 已知函数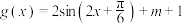 在区间
在区间 上的最大值为3.
上的最大值为3.
(1)求 的值;
的值;
(2)当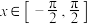 时,
时,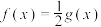 ,对于给定的实数
,对于给定的实数 ,若方程
,若方程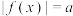 有解,则记该方程所有解的和为
有解,则记该方程所有解的和为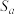 ,求
,求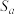 的所有可能取值.
的所有可能取值.
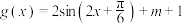 在区间
在区间 上的最大值为3.
上的最大值为3.(1)求
 的值;
的值;(2)当
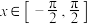 时,
时,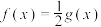 ,对于给定的实数
,对于给定的实数 ,若方程
,若方程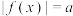 有解,则记该方程所有解的和为
有解,则记该方程所有解的和为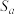 ,求
,求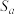 的所有可能取值.
的所有可能取值.
您最近半年使用:0次
10 . 将余弦函数 的图象上所有点的纵坐标伸长到原来的
的图象上所有点的纵坐标伸长到原来的 倍(横坐标不变),再将所得到的图象向右平移
倍(横坐标不变),再将所得到的图象向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象.若关于x的方程
的图象.若关于x的方程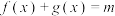 在
在 内有两个不同的解,则实数m的取值范围为
内有两个不同的解,则实数m的取值范围为___________ .
 的图象上所有点的纵坐标伸长到原来的
的图象上所有点的纵坐标伸长到原来的 倍(横坐标不变),再将所得到的图象向右平移
倍(横坐标不变),再将所得到的图象向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象.若关于x的方程
的图象.若关于x的方程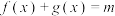 在
在 内有两个不同的解,则实数m的取值范围为
内有两个不同的解,则实数m的取值范围为
您最近半年使用:0次



