解题方法
1 . 函数 的最大值为( )
的最大值为( )
 的最大值为( )
的最大值为( )A.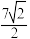 | B.4 | C.3 | D.5 |
您最近半年使用:0次
名校
解题方法
2 . 已知函数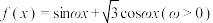 .
.
(1)当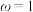 时,求
时,求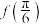 的值;
的值;
(2)当函数 图像的两条相邻对称轴之间的距离是
图像的两条相邻对称轴之间的距离是 时,______.
时,______.
从①②③中任选一个,补充到上面空格处并作答.
①求 在区间
在区间 上的最小值;
上的最小值;
②求 的单调递增区间;
的单调递增区间;
③若 ,求
,求 的取值范围.
的取值范围.
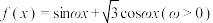 .
.(1)当
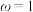 时,求
时,求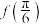 的值;
的值;(2)当函数
 图像的两条相邻对称轴之间的距离是
图像的两条相邻对称轴之间的距离是 时,______.
时,______.从①②③中任选一个,补充到上面空格处并作答.
①求
 在区间
在区间 上的最小值;
上的最小值;②求
 的单调递增区间;
的单调递增区间;③若
 ,求
,求 的取值范围.
的取值范围.
您最近半年使用:0次
3 . 已知函数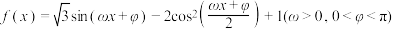 的图象过原点,且图象的相邻两对称轴间的距离为
的图象过原点,且图象的相邻两对称轴间的距离为 .
.
(1)求函数 的解析式;
的解析式;
(2)若函数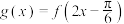 ,记方程
,记方程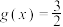 在
在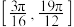 上的根从小到大依次为
上的根从小到大依次为 ,试确定
,试确定 的值,并求
的值,并求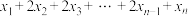 的值.
的值.
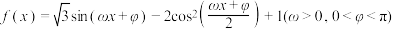 的图象过原点,且图象的相邻两对称轴间的距离为
的图象过原点,且图象的相邻两对称轴间的距离为 .
.(1)求函数
 的解析式;
的解析式;(2)若函数
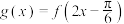 ,记方程
,记方程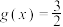 在
在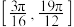 上的根从小到大依次为
上的根从小到大依次为 ,试确定
,试确定 的值,并求
的值,并求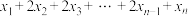 的值.
的值.
您最近半年使用:0次
名校
解题方法
4 . 已知函数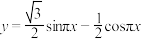 在
在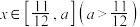 上的最小值为
上的最小值为 ,最大值为
,最大值为 ,若
,若 ,则实数
,则实数 的取值范围为
的取值范围为__________ .
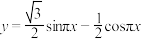 在
在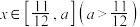 上的最小值为
上的最小值为 ,最大值为
,最大值为 ,若
,若 ,则实数
,则实数 的取值范围为
的取值范围为
您最近半年使用:0次
2023高三·全国·专题练习
解题方法
5 . 在 中,角A,B,C所对的边分别为a,b,c,
中,角A,B,C所对的边分别为a,b,c, .
.
(1)求B;
(2)若点D为边BC的中点,点E,F分别在边AB,AC上,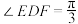 ,
,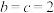 .设
.设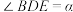 ,将
,将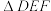 的面积
的面积 表示为
表示为 的函数,并求
的函数,并求 的取值范围.
的取值范围.
 中,角A,B,C所对的边分别为a,b,c,
中,角A,B,C所对的边分别为a,b,c, .
.(1)求B;
(2)若点D为边BC的中点,点E,F分别在边AB,AC上,
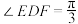 ,
,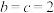 .设
.设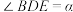 ,将
,将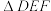 的面积
的面积 表示为
表示为 的函数,并求
的函数,并求 的取值范围.
的取值范围.
您最近半年使用:0次
解题方法
6 . 已知函数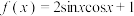 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 的最大值.
的最大值.
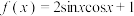 .
.(1)求函数
 的最小正周期;
的最小正周期;(2)求函数
 的最大值.
的最大值.
您最近半年使用:0次
名校
解题方法
7 . 关于函数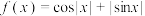 的下述四个结论中,正确的有( )
的下述四个结论中,正确的有( )
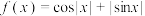 的下述四个结论中,正确的有( )
的下述四个结论中,正确的有( )A. 是偶函数 是偶函数 | B. 的最大值为 的最大值为 |
C. 在 在 有 有 个零点 个零点 | D. 在区间 在区间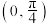 单调递增 单调递增 |
您最近半年使用:0次
8 . 若函数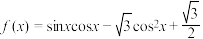 ,则下列结论正确的是( )
,则下列结论正确的是( )
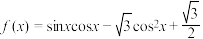 ,则下列结论正确的是( )
,则下列结论正确的是( )A.函数 的最小正周期为 的最小正周期为 |
B.函数 在区间 在区间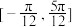 上单调递增 上单调递增 |
C.函数 图象关于 图象关于 对称 对称 |
D.函数 的图象关于点 的图象关于点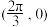 对称 对称 |
您最近半年使用:0次
2023-08-13更新
|
480次组卷
|
2卷引用:四川省绵阳市南山中学实验学校2022-2023学年高一下学期期中考试数学试题
9 . 已知函数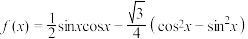 ,
, .
.
(1)求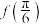 的值;
的值;
(2)求 的单调递增区间.
的单调递增区间.
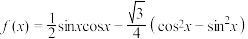 ,
, .
.(1)求
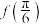 的值;
的值;(2)求
 的单调递增区间.
的单调递增区间.
您最近半年使用:0次
解题方法
10 . 已知函数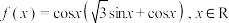 .
.
(1)当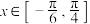 时,求函数
时,求函数 的最大值;
的最大值;
(2)若 ,求
,求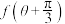 的值.
的值.
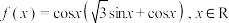 .
.(1)当
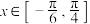 时,求函数
时,求函数 的最大值;
的最大值;(2)若
 ,求
,求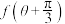 的值.
的值.
您最近半年使用:0次



