名校
解题方法
1 . 已知数列 的前
的前 项和为
项和为 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和 .
.
您最近半年使用:0次
解题方法
2 . 数列 的前
的前 项和
项和 满足
满足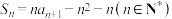 .
.
(1)证明: 是等差数列;
是等差数列;
(2)若 ,证明:
,证明: .
.
 的前
的前 项和
项和 满足
满足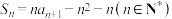 .
.(1)证明:
 是等差数列;
是等差数列;(2)若
 ,证明:
,证明: .
.
您最近半年使用:0次
解题方法
3 . 已知数列 的前n项和为
的前n项和为 ,
, ,
,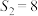 ,且当
,且当 时,
时,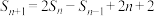 .
.
(1)求 ;
;
(2)设数列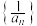 的前n项和为
的前n项和为 ,证明:
,证明: .
.
 的前n项和为
的前n项和为 ,
, ,
,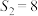 ,且当
,且当 时,
时,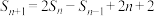 .
.(1)求
 ;
;(2)设数列
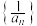 的前n项和为
的前n项和为 ,证明:
,证明: .
.
您最近半年使用:0次
名校
解题方法
4 . 已知 为数列
为数列 的前n项和,满足
的前n项和,满足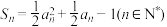 ,且
,且 成等比数列,当
成等比数列,当 时,
时, .
.
(1)求证:当 时,
时, 成等差数列;
成等差数列;
(2)求 的前n项和
的前n项和 .
.
 为数列
为数列 的前n项和,满足
的前n项和,满足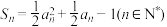 ,且
,且 成等比数列,当
成等比数列,当 时,
时, .
.(1)求证:当
 时,
时, 成等差数列;
成等差数列;(2)求
 的前n项和
的前n项和 .
.
您最近半年使用:0次
名校
解题方法
5 . 数列 的前
的前 项和记为
项和记为 ,若
,若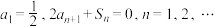 ,则
,则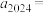
______ .
 的前
的前 项和记为
项和记为 ,若
,若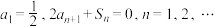 ,则
,则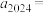
您最近半年使用:0次
解题方法
6 . 已知数列 中,
中, 为
为 的前
的前 项和,
项和,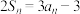 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令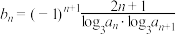 ,求数列
,求数列 的前
的前 项和
项和 .
.
 中,
中, 为
为 的前
的前 项和,
项和,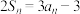 .
.(1)求数列
 的通项公式;
的通项公式;(2)令
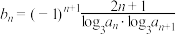 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近半年使用:0次
名校
解题方法
7 . 已知数列 的前
的前 项和为
项和为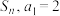 ,且
,且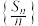 为等差数列.
为等差数列.
(1)证明: 为等差数列;
为等差数列;
(2)若 ,数列
,数列 满足
满足 ,且
,且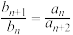 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为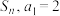 ,且
,且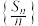 为等差数列.
为等差数列.(1)证明:
 为等差数列;
为等差数列;(2)若
 ,数列
,数列 满足
满足 ,且
,且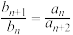 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近半年使用:0次
解题方法
8 . 已知正项数列 的前n项和为
的前n项和为 ,且
,且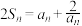 ,数列
,数列 的前n项积为
的前n项积为 且
且 ,下列说法错误的是( )
,下列说法错误的是( )
 的前n项和为
的前n项和为 ,且
,且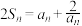 ,数列
,数列 的前n项积为
的前n项积为 且
且 ,下列说法错误的是( )
,下列说法错误的是( )A.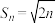 | B. 为递减数列 为递减数列 |
C.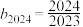 | D. |
您最近半年使用:0次
7日内更新
|
226次组卷
|
3卷引用:陕西省汉中市2023-2024学年高三下学期教学质量第二次检测理科数学试卷
陕西省汉中市2023-2024学年高三下学期教学质量第二次检测理科数学试卷陕西省汉中市2023-2024学年高三下学期教学质量第二次检测文科数学试卷(已下线)模块五 专题6 全真拔高模拟6(人教B版高二期中研习)
解题方法
9 . 已知 为正项数列
为正项数列 的前
的前 项和,
项和, 且
且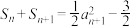 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若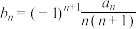 ,求
,求 的前10项和
的前10项和 .
.
 为正项数列
为正项数列 的前
的前 项和,
项和, 且
且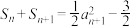 .
.(1)求数列
 的通项公式;
的通项公式;(2)若
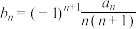 ,求
,求 的前10项和
的前10项和 .
.
您最近半年使用:0次
解题方法
10 . 设数列 的前n项和为
的前n项和为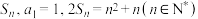 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前n项和为
的前n项和为 ,且
,且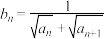 ,求
,求 ;
;
(3)证明: .
.
 的前n项和为
的前n项和为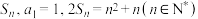 .
.(1)求数列
 的通项公式;
的通项公式;(2)设数列
 的前n项和为
的前n项和为 ,且
,且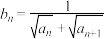 ,求
,求 ;
;(3)证明:
 .
.
您最近半年使用:0次



