1 . 数列 满足
满足 ,对任意
,对任意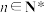 ,都有
,都有 ,数列
,数列 前n项和为
前n项和为 ,则下列结论正确的是( )
,则下列结论正确的是( )
 满足
满足 ,对任意
,对任意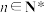 ,都有
,都有 ,数列
,数列 前n项和为
前n项和为 ,则下列结论正确的是( )
,则下列结论正确的是( )A. | B. 与 与 等差中项为6 等差中项为6 |
C.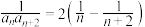 | D.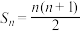 |
您最近半年使用:0次
解题方法
2 . 已知数列 是有无穷项的等差数列,
是有无穷项的等差数列,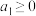 ,公差
,公差 ,若满足条件:①
,若满足条件:① 是数列
是数列 的项;②对任意的正整数
的项;②对任意的正整数
 ,都存在正整数
,都存在正整数 ,使得
,使得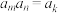 .则满足这样的数列的个数是
.则满足这样的数列的个数是______ 种.
 是有无穷项的等差数列,
是有无穷项的等差数列,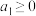 ,公差
,公差 ,若满足条件:①
,若满足条件:① 是数列
是数列 的项;②对任意的正整数
的项;②对任意的正整数
 ,都存在正整数
,都存在正整数 ,使得
,使得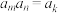 .则满足这样的数列的个数是
.则满足这样的数列的个数是
您最近半年使用:0次
3 . 已知正项数列 的前
的前 项和为
项和为 ,
,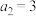 ,且
,且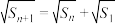 .
.
(1)求 的通项公式;
的通项公式;
(2)若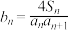 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,
,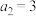 ,且
,且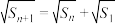 .
.(1)求
 的通项公式;
的通项公式;(2)若
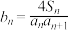 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近半年使用:0次
4 . 已知函数 的图象关于点
的图象关于点 中心对称,也关于点
中心对称,也关于点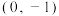 中心对称,则
中心对称,则 的中位数为
的中位数为__________ .
 的图象关于点
的图象关于点 中心对称,也关于点
中心对称,也关于点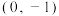 中心对称,则
中心对称,则 的中位数为
的中位数为
您最近半年使用:0次
名校
解题方法
5 . 垛积术是古代数学技术,常用于计算物品按规律堆积时的数目.如下图,三角垛指的是顶层放1个,第二层放3个,第三层放6个,第四层放10个,……,第n层放 个物体堆成的堆垛.若
个物体堆成的堆垛.若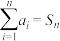 ,则下列说法正确的是( )
,则下列说法正确的是( )
 个物体堆成的堆垛.若
个物体堆成的堆垛.若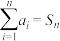 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.数列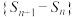 是等差数列 是等差数列 |
B.数列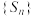 的通项公式是一个关于n的2次多项式 的通项公式是一个关于n的2次多项式 |
C.数列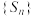 的通项公式是一个关于n的3次多项式 的通项公式是一个关于n的3次多项式 |
D.数列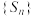 的通项公式是一个关于n的4次多项式 的通项公式是一个关于n的4次多项式 |
您最近半年使用:0次
23-24高二下·全国·课前预习
解题方法
6 . 等差数列前 项和的性质
项和的性质
(1)若数列 是公差为
是公差为 的等差数列,则数列
的等差数列,则数列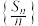 也是等差数列,且公差为
也是等差数列,且公差为______ .
(2)若 分别为等差数列
分别为等差数列 的前
的前 项,前
项,前 项,前
项,前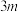 项的和,则
项的和,则 ,
, 也成等差数列,公差为
也成等差数列,公差为______ .
(3)设两个等差数列 的前
的前 项和分别为
项和分别为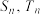 ,则
,则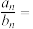
______ .
(4)在等差数列中,若 ,则
,则
______ .
 项和的性质
项和的性质(1)若数列
 是公差为
是公差为 的等差数列,则数列
的等差数列,则数列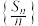 也是等差数列,且公差为
也是等差数列,且公差为(2)若
 分别为等差数列
分别为等差数列 的前
的前 项,前
项,前 项,前
项,前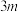 项的和,则
项的和,则 ,
, 也成等差数列,公差为
也成等差数列,公差为(3)设两个等差数列
 的前
的前 项和分别为
项和分别为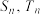 ,则
,则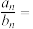
(4)在等差数列中,若
 ,则
,则
您最近半年使用:0次
解题方法
7 . 已知正项数列 的前n项和为
的前n项和为 ,且
,且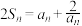 ,数列
,数列 的前n项积为
的前n项积为 且
且 ,下列说法错误的是( )
,下列说法错误的是( )
 的前n项和为
的前n项和为 ,且
,且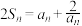 ,数列
,数列 的前n项积为
的前n项积为 且
且 ,下列说法错误的是( )
,下列说法错误的是( )A.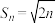 | B. 为递减数列 为递减数列 |
C.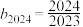 | D. |
您最近半年使用:0次
7日内更新
|
257次组卷
|
3卷引用:陕西省汉中市2023-2024学年高三下学期教学质量第二次检测理科数学试卷
陕西省汉中市2023-2024学年高三下学期教学质量第二次检测理科数学试卷陕西省汉中市2023-2024学年高三下学期教学质量第二次检测文科数学试卷(已下线)模块五 专题6 全真拔高模拟6(人教B版高二期中研习)
8 . 已知数列 的前n项和为
的前n项和为 ,则“数列
,则“数列 为等差数列”的充要条件是( )
为等差数列”的充要条件是( )
 的前n项和为
的前n项和为 ,则“数列
,则“数列 为等差数列”的充要条件是( )
为等差数列”的充要条件是( )A.当 时, 时,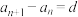 ( ( 为常数) 为常数) | B. ( ( , , 为常数) 为常数) |
C. ( ( , , 为常数) 为常数) | D. |
您最近半年使用:0次
9 . 已知数列 满足:
满足: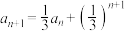 ,且
,且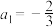 .设
.设 的前
的前 项和为
项和为 ,
,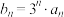 .
.
(1)证明: 是等差数列;
是等差数列;
(2)求 ;
;
(3)若不等式 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 满足:
满足: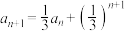 ,且
,且 .设
.设 的前
的前 项和为
项和为 ,
,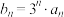 .
.(1)证明:
 是等差数列;
是等差数列;(2)求
 ;
;(3)若不等式
 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
10 . 数列 是各项为正数的等比数列,其前
是各项为正数的等比数列,其前 项和为
项和为 ,下列说法错误的是( )
,下列说法错误的是( )
 是各项为正数的等比数列,其前
是各项为正数的等比数列,其前 项和为
项和为 ,下列说法错误的是( )
,下列说法错误的是( )A.数列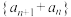 是等比数列 是等比数列 | B.数列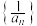 是等比数列 是等比数列 |
C.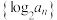 是等差数列 是等差数列 | D.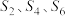 成等比数列 成等比数列 |
您最近半年使用:0次



