名校
解题方法
1 . 已知 为数列
为数列 的前
的前 和,下列说法正确的是( )
和,下列说法正确的是( )
 为数列
为数列 的前
的前 和,下列说法正确的是( )
和,下列说法正确的是( )A.若数列 为等差数列,则 为等差数列,则  , , , , 为等差数列 为等差数列 |
B.若 为等比数列,则 为等比数列,则 , , , , 为等比数列 为等比数列 |
C.若 为等差数列,则 为等差数列,则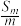 , ,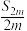 , , 为等差数列 为等差数列 |
D.若 为等比数列,则 为等比数列,则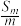 , ,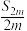 , ,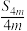 为等比数列 为等比数列 |
您最近半年使用:0次
名校
解题方法
2 . 已知等差数列 的前
的前 项和为
项和为 ,且满足
,且满足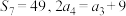 ,数列
,数列 满足
满足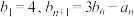 .
.
(1)证明:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(2)已知数列 满足
满足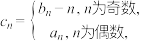 求数列
求数列 的前
的前 项和
项和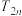 .
.
 的前
的前 项和为
项和为 ,且满足
,且满足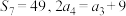 ,数列
,数列 满足
满足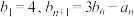 .
.(1)证明:数列
 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;(2)已知数列
 满足
满足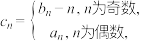 求数列
求数列 的前
的前 项和
项和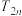 .
.
您最近半年使用:0次
2023-12-04更新
|
2009次组卷
|
5卷引用:湖南省长沙市长郡中学2024届高三上学期月考(四)数学试题
湖南省长沙市长郡中学2024届高三上学期月考(四)数学试题广东省普宁市勤建学校2024届高三上学期第三次调研数学试题安徽省皖中名校联盟2024届高三上学期第五次联考数学试题(已下线)专题04 数列及求和(讲义)(已下线)专题09 数列的通项公式、数列求和及综合应用(练习)-2
名校
解题方法
3 . 已知公比为2的等比数列 的前n项和为
的前n项和为 ,且
,且 ,
,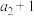 ,
,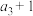 成等差数列,则
成等差数列,则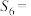 ( )
( )
 的前n项和为
的前n项和为 ,且
,且 ,
,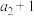 ,
,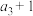 成等差数列,则
成等差数列,则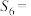 ( )
( )| A.64 | B.63 | C.126 | D.128 |
您最近半年使用:0次
2023-11-10更新
|
1749次组卷
|
5卷引用:广东省汕头市潮阳实验学校2024届高三上学期摸底数学试题
广东省汕头市潮阳实验学校2024届高三上学期摸底数学试题(已下线)专题14 数列的基本量计算【讲】(已下线)第一篇“必拿”选择前5填空前2 专题14 数列的基本量计算【讲】山东省临沂市临沭第一中学2023-2024学年高二上学期第二次教学质量检测数学试题(已下线)专题04 数列及求和(讲义)
解题方法
4 . 设数列 的前n项和为
的前n项和为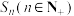 ,关于数列
,关于数列 有下列四个命题:
有下列四个命题:
①若 既是等差数列又是等比数列,则
既是等差数列又是等比数列,则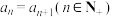
②若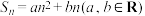 ,则
,则 是等差数列
是等差数列
③若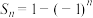 ,则
,则 是等比数列
是等比数列
④若 是等比数列,则
是等比数列,则 也成等比数列.
也成等比数列.
其中正确命题的序号是__________ .(填上所有正确命题的序号)
 的前n项和为
的前n项和为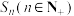 ,关于数列
,关于数列 有下列四个命题:
有下列四个命题:①若
 既是等差数列又是等比数列,则
既是等差数列又是等比数列,则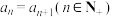
②若
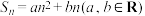 ,则
,则 是等差数列
是等差数列③若
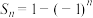 ,则
,则 是等比数列
是等比数列④若
 是等比数列,则
是等比数列,则 也成等比数列.
也成等比数列.其中正确命题的序号是
您最近半年使用:0次
名校
解题方法
5 . 已知数列 的前
的前 项和为
项和为 ,下列说法正确的是( )
,下列说法正确的是( )
 的前
的前 项和为
项和为 ,下列说法正确的是( )
,下列说法正确的是( )A.若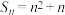 ,则 ,则 是等差数列 是等差数列 |
B.若 是等比数列,且 是等比数列,且 , , ,则 ,则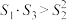 |
C.若 是等差数列,则 是等差数列,则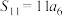 |
D.若 ,则 ,则 是等比数列 是等比数列 |
您最近半年使用:0次
2023-04-13更新
|
434次组卷
|
3卷引用:湖北省云学新高考联盟学校2022-2023学年高二下学期4月期中联考数学试题
湖北省云学新高考联盟学校2022-2023学年高二下学期4月期中联考数学试题湖南省益阳市安化县第二中学2022-2023学年高二上学期期中数学试题(已下线)4.3.2等比数列的前n项和公式(第2课时)(分层作业)(3种题型)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第二册)
名校
解题方法
6 . 记 为数列
为数列 的前
的前 项和,下列说法正确的是( )
项和,下列说法正确的是( )
 为数列
为数列 的前
的前 项和,下列说法正确的是( )
项和,下列说法正确的是( )A.若对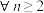 , , ,有 ,有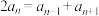 ,则数列 ,则数列 一定是等差数列 一定是等差数列 |
B.若对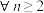 , , ,有 ,有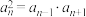 ,则数列 ,则数列 一定是等比数列 一定是等比数列 |
C.已知 ,则 ,则 一定是等差数列 一定是等差数列 |
D.已知 ,则 ,则 一定是等比数列 一定是等比数列 |
您最近半年使用:0次
2023-02-22更新
|
612次组卷
|
4卷引用:广东省广州市铁一中学等三校2022-2023学年高二上学期期末联考数学试题
广东省广州市铁一中学等三校2022-2023学年高二上学期期末联考数学试题辽宁省铁岭市清河高级中学2022-2023学年高二下学期3月月考数学试题1.3等比数列 测试卷(已下线)高二数学第一学期期期末押题密卷04卷
名校
解题方法
7 . 设等比数列 的首项为1,公比为q,
的首项为1,公比为q, 是数列
是数列 的前n项和,则“
的前n项和,则“ ”是“
”是“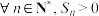 恒成立”的( )
恒成立”的( )
 的首项为1,公比为q,
的首项为1,公比为q, 是数列
是数列 的前n项和,则“
的前n项和,则“ ”是“
”是“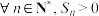 恒成立”的( )
恒成立”的( )| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
2023-02-16更新
|
655次组卷
|
5卷引用:云南师范大学附属中学2023届高三第七次月考数学试题
云南师范大学附属中学2023届高三第七次月考数学试题河南省新乡市第一中学2022-2023学年高二下学期3月月考数学试题(已下线)江苏省南通市如皋市2023-2024学年高三上学期8月诊断测试数学试题(已下线)模块一 专题6 数列(2)(人教A)四川省绵阳中学2023届高三适应性考试(三)理科数学试题
解题方法
8 . 已知数列 为等比数列,且
为等比数列,且 是
是 与
与 的等差中项,若
的等差中项,若 ,则该数列的前5项和为( )
,则该数列的前5项和为( )
 为等比数列,且
为等比数列,且 是
是 与
与 的等差中项,若
的等差中项,若 ,则该数列的前5项和为( )
,则该数列的前5项和为( )| A.2 | B.10 | C.31 | D.62 |
您最近半年使用:0次
2023-02-13更新
|
498次组卷
|
4卷引用:山东省济宁市2022-2023学年高二上学期期末数学试题
名校
解题方法
9 . 下列命题判断中,正确的是( )
A.命题 : : ,命题 ,命题 : :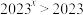 ,则 ,则 是 是 的必要不充分条件 的必要不充分条件 |
B.当 时,幂函数 时,幂函数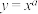 在区间 在区间 上单调递减 上单调递减 |
C.若直线 的倾斜角大于 的倾斜角大于 ,那么它的斜率大于 ,那么它的斜率大于 |
D.若数列 的前 的前 项和为 项和为 ,则数列 ,则数列 是等比数列 是等比数列 |
您最近半年使用:0次
名校
解题方法
10 . 已知数列 的前n项和为
的前n项和为 ,且
,且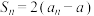 (其中a为常数),则下列说法正确的是( )
(其中a为常数),则下列说法正确的是( )
 的前n项和为
的前n项和为 ,且
,且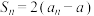 (其中a为常数),则下列说法正确的是( )
(其中a为常数),则下列说法正确的是( )A.数列 一定是等比数列 一定是等比数列 | B.数列 可能是等差数列 可能是等差数列 |
C.数列 可能是等比数列 可能是等比数列 | D.数列 可能是等差数列 可能是等差数列 |
您最近半年使用:0次
2023-01-16更新
|
359次组卷
|
10卷引用:江苏省苏州市2019-2020学年高二上学期期末数学试题
江苏省苏州市2019-2020学年高二上学期期末数学试题(已下线)专题07 数列(1)-2020年新高考新题型多项选择题专项训练江苏省常州市前黄高级中学2020-2021学年高三上学期期中适应性考试数学试题江苏省苏州大学附属中学2020-2021学年高二上学期12月检测数学试题(已下线)第四章 数列-2020-2021学年高二数学同步课堂帮帮帮(人教A版2019选择性必修第二册)(已下线)“8+4+4”小题强化训练(28)数列的概念及表示法-2022届高考数学一轮复习(江苏等新高考地区专用)人教B版(2019) 选修第三册 一蹴而就 第五章 5.3.2 等比数列的前n项和 第一课时 等比数列的前n项和(1)浙江省杭州市桐庐中学2022-2023学年新高三暑期阶段性测试数学试题河北省石家庄二中教育集团2022-2023学年高二上学期期末四校联考数学试题河北省衡水市武邑中学2024届高三上学期第三次调研考试数学试题



