1 . 已知等比数列 的首项为
的首项为 ,公比
,公比 为整数,且
为整数,且 .
.
(1)求 的通项公式;
的通项公式;
(2)设数列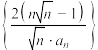 的前
的前 项和为
项和为 ,比较
,比较 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
 的首项为
的首项为 ,公比
,公比 为整数,且
为整数,且 .
.(1)求
 的通项公式;
的通项公式;(2)设数列
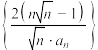 的前
的前 项和为
项和为 ,比较
,比较 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
您最近半年使用:0次
昨日更新
|
386次组卷
|
2卷引用:河南省濮阳市2024届高三下学期(开学)第一次模拟考试数学试题
解题方法
2 . 在数列 中,已知
中,已知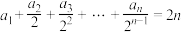 .
.
(1)求数列 的通项公式;
的通项公式;
(2)在数列 中的
中的 和
和 之间插入1个数
之间插入1个数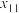 ,使
,使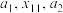 成等差数列;在
成等差数列;在 和
和 之间插入2个数
之间插入2个数 ,使
,使 成等差数列;…;在
成等差数列;…;在 和
和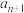 之间插入
之间插入 个数
个数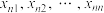 ,使
,使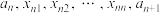 成等差数列,这样可以得到新数列
成等差数列,这样可以得到新数列 ,设数列
,设数列 的前
的前 项和为
项和为 ,求
,求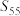 (用数字作答).
(用数字作答).
 中,已知
中,已知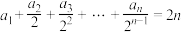 .
.(1)求数列
 的通项公式;
的通项公式;(2)在数列
 中的
中的 和
和 之间插入1个数
之间插入1个数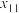 ,使
,使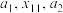 成等差数列;在
成等差数列;在 和
和 之间插入2个数
之间插入2个数 ,使
,使 成等差数列;…;在
成等差数列;…;在 和
和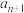 之间插入
之间插入 个数
个数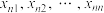 ,使
,使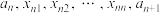 成等差数列,这样可以得到新数列
成等差数列,这样可以得到新数列 ,设数列
,设数列 的前
的前 项和为
项和为 ,求
,求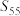 (用数字作答).
(用数字作答).
您最近半年使用:0次
2024·全国·模拟预测
3 . 已知数列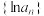 为等差数列,且
为等差数列,且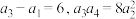 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足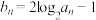 ,记
,记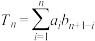 ,求
,求 .
.
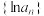 为等差数列,且
为等差数列,且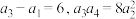 .
.(1)求数列
 的通项公式;
的通项公式;(2)若数列
 满足
满足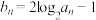 ,记
,记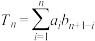 ,求
,求 .
.
您最近半年使用:0次
解题方法
4 . 设数列 ,
, 的前n项和分别为
的前n项和分别为 ,
, ,
, ,
, ,且
,且 ,
,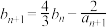 (
( ).
).
(1)求 的通项公式,并证明:
的通项公式,并证明: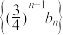 是等差数列;
是等差数列;
(2)若不等式 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 ,
, 的前n项和分别为
的前n项和分别为 ,
, ,
, ,
, ,且
,且 ,
,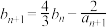 (
( ).
).(1)求
 的通项公式,并证明:
的通项公式,并证明: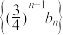 是等差数列;
是等差数列;(2)若不等式
 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
5 . 已知数列 满足:
满足: .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 的前
的前 项和
项和 满足
满足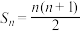 ,求数列
,求数列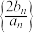 的前
的前 项和
项和 ,并求
,并求 的取值范围.
的取值范围.
 满足:
满足: .
.(1)求数列
 的通项公式;
的通项公式;(2)若数列
 的前
的前 项和
项和 满足
满足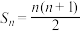 ,求数列
,求数列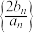 的前
的前 项和
项和 ,并求
,并求 的取值范围.
的取值范围.
您最近半年使用:0次
名校
解题方法
6 . 已知等差数列 的前
的前 项和为
项和为 ,
,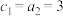 且
且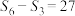 ,数列
,数列 满足
满足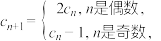 ,设
,设 .
.
(1)求 的通项公式,并证明:
的通项公式,并证明: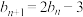 ;
;
(2)设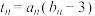 ,求数列
,求数列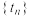 的前
的前 项和
项和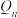 .
.
 的前
的前 项和为
项和为 ,
,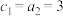 且
且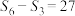 ,数列
,数列 满足
满足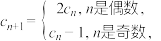 ,设
,设 .
.(1)求
 的通项公式,并证明:
的通项公式,并证明: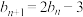 ;
;(2)设
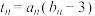 ,求数列
,求数列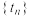 的前
的前 项和
项和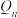 .
.
您最近半年使用:0次
7 . 已知数列 满足
满足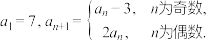
(1)写出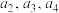 ;
;
(2)证明:数列 为等比数列;
为等比数列;
(3)若 ,求数列
,求数列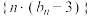 的前
的前 项和
项和 .
.
 满足
满足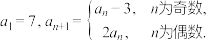
(1)写出
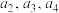 ;
;(2)证明:数列
 为等比数列;
为等比数列;(3)若
 ,求数列
,求数列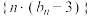 的前
的前 项和
项和 .
.
您最近半年使用:0次
解题方法
8 . 已知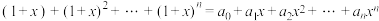 ,且存在正整数
,且存在正整数 ,满足
,满足 ,则下列结论正确的是( )
,则下列结论正确的是( )
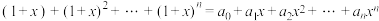 ,且存在正整数
,且存在正整数 ,满足
,满足 ,则下列结论正确的是( )
,则下列结论正确的是( )A. |
B.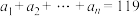 |
C. 展开式中所有项系数和为126 展开式中所有项系数和为126 |
D.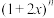 展开式中二项式系数最大的项为第三项和第四项 展开式中二项式系数最大的项为第三项和第四项 |
您最近半年使用:0次
9 . 已知等比数列 的前n项和为
的前n项和为 ,且
,且 的前3项和为
的前3项和为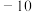 ,
, 的前6项和为78.
的前6项和为78.
(1)求数列 的通项公式
的通项公式 及前n项和
及前n项和 ;
;
(2)若数列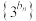 为首项为1,公比为3的等比数列,求数列
为首项为1,公比为3的等比数列,求数列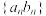 的前n项和
的前n项和 .
.
 的前n项和为
的前n项和为 ,且
,且 的前3项和为
的前3项和为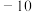 ,
, 的前6项和为78.
的前6项和为78.(1)求数列
 的通项公式
的通项公式 及前n项和
及前n项和 ;
;(2)若数列
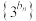 为首项为1,公比为3的等比数列,求数列
为首项为1,公比为3的等比数列,求数列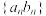 的前n项和
的前n项和 .
.
您最近半年使用:0次
10 . 已知数列 的前
的前 项和为
项和为 ,
, ,且
,且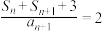 .
.
(1)证明:数列 为等比数列,并求其通项公式;
为等比数列,并求其通项公式;
(2)若__________,求数列 的前
的前 项和
项和 .
.
从① ;②
;②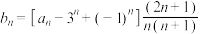 ;③
;③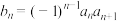 ,这三个条件中任选一个补充在上而的横线上并解答问题,注:如果选择多个条件分别解答,按第一个解答计分.
,这三个条件中任选一个补充在上而的横线上并解答问题,注:如果选择多个条件分别解答,按第一个解答计分.
 的前
的前 项和为
项和为 ,
, ,且
,且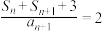 .
.(1)证明:数列
 为等比数列,并求其通项公式;
为等比数列,并求其通项公式;(2)若__________,求数列
 的前
的前 项和
项和 .
.从①
 ;②
;②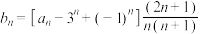 ;③
;③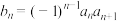 ,这三个条件中任选一个补充在上而的横线上并解答问题,注:如果选择多个条件分别解答,按第一个解答计分.
,这三个条件中任选一个补充在上而的横线上并解答问题,注:如果选择多个条件分别解答,按第一个解答计分.
您最近半年使用:0次



