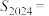1 . 已知数列 满足:
满足: ,
, ;数列
;数列 是各项都为正数的等比数列且满足
是各项都为正数的等比数列且满足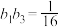 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)记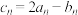 ,求数列
,求数列 的前
的前 项和
项和 .
.
 满足:
满足: ,
, ;数列
;数列 是各项都为正数的等比数列且满足
是各项都为正数的等比数列且满足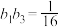 ,
, .
.(1)求数列
 ,
, 的通项公式;
的通项公式;(2)记
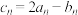 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近半年使用:0次
2 . 已知等比数列 的前
的前 项和为
项和为 ,
, ,且
,且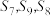 成等差数列.
成等差数列.
(1)求 ;
;
(2)设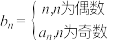 ,
, 是数列
是数列 的前
的前 项和,求
项和,求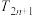 ;
;
(3)设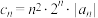 ,
,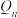 是
是 的前
的前 项的积,求证:
项的积,求证: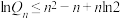 (
( 为正整数).
为正整数).
 的前
的前 项和为
项和为 ,
, ,且
,且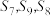 成等差数列.
成等差数列.(1)求
 ;
;(2)设
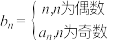 ,
, 是数列
是数列 的前
的前 项和,求
项和,求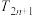 ;
;(3)设
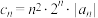 ,
,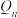 是
是 的前
的前 项的积,求证:
项的积,求证: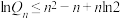 (
( 为正整数).
为正整数).
您最近半年使用:0次
3 . 记数列 的前
的前 项和为
项和为 ,已知
,已知 ,且
,且 .
.
(1)令 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若对于任意的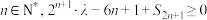 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的前
的前 项和为
项和为 ,已知
,已知 ,且
,且 .
.(1)令
 ,求数列
,求数列 的通项公式;
的通项公式;(2)若对于任意的
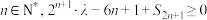 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
4 . 已知数列 满足
满足 ,
, ,设
,设 的前n项和为
的前n项和为 ,下列结论正确的( )
,下列结论正确的( )
 满足
满足 ,
, ,设
,设 的前n项和为
的前n项和为 ,下列结论正确的( )
,下列结论正确的( )A.数列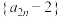 是等比数列 是等比数列 | B. |
C.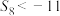 | D.当 时,数列 时,数列 是单调递减数列 是单调递减数列 |
您最近半年使用:0次
昨日更新
|
826次组卷
|
5卷引用:江西省部分学校2023-2024学年高二下学期3月联考数学试卷
名校
解题方法
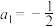
5 . 已知等比数列 的前n项和为
的前n项和为 ,
, ,且
,且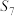 ,
, ,
,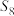 成等差数列.
成等差数列.
(1)求 ;
;
(2)设 ,
, 是数列
是数列 的前n项和,求
的前n项和,求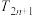 ;
;
(3)设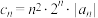 ,
,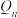 是
是 的前n项的积,求证:
的前n项的积,求证: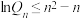 ,
, .
.
 的前n项和为
的前n项和为 ,
, ,且
,且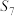 ,
, ,
,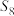 成等差数列.
成等差数列.(1)求
 ;
;(2)设
 ,
, 是数列
是数列 的前n项和,求
的前n项和,求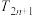 ;
;(3)设
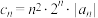 ,
,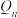 是
是 的前n项的积,求证:
的前n项的积,求证: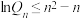 ,
, .
.
您最近半年使用:0次
6 . 已知数列 的首项
的首项 ,且满足
,且满足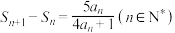 .
.
(1)判断数列 是否为等比数列;
是否为等比数列;
(2)若 ,记数列
,记数列 的前
的前 项和为
项和为 ,求
,求 .
.
 的首项
的首项 ,且满足
,且满足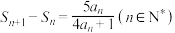 .
.(1)判断数列
 是否为等比数列;
是否为等比数列;(2)若
 ,记数列
,记数列 的前
的前 项和为
项和为 ,求
,求 .
.
您最近半年使用:0次
7 . 已知各项均为正数的数列 的前n项和为
的前n项和为 ,
, ,
, ,
, ,则
,则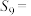 ( )
( )
 的前n项和为
的前n项和为 ,
, ,
, ,
, ,则
,则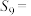 ( )
( )| A.511 | B.61 | C.41 | D.9 |
您最近半年使用:0次
2024·全国·模拟预测
8 . 数列 满足
满足 ,
, ,且
,且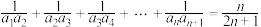 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设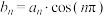 ,求数列
,求数列 的前
的前 项和
项和 .
.
 满足
满足 ,
, ,且
,且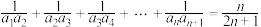 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
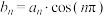 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近半年使用:0次
9 . 已知数列 满足
满足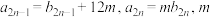 为常数,若
为常数,若 为等差数列,且
为等差数列,且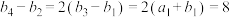 .
.
(1)求 的值及
的值及 的通项公式;
的通项公式;
(2)求 的前
的前 项和
项和 .
.
 满足
满足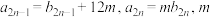 为常数,若
为常数,若 为等差数列,且
为等差数列,且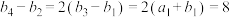 .
.(1)求
 的值及
的值及 的通项公式;
的通项公式;(2)求
 的前
的前 项和
项和 .
.
您最近半年使用:0次

 项和第
项和第 项之间插入
项之间插入 ,得到新数列
,得到新数列