解题方法
1 . 如图,在四棱台 中,底面四边形
中,底面四边形 为菱形,
为菱形, ,
, 平面
平面 .
.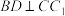 ;
;
(2)若四棱台 的体积为
的体积为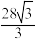 ,求点
,求点 到平面
到平面 的距离.
的距离.
 中,底面四边形
中,底面四边形 为菱形,
为菱形, ,
, 平面
平面 .
.
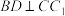 ;
;(2)若四棱台
 的体积为
的体积为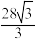 ,求点
,求点 到平面
到平面 的距离.
的距离.
您最近半年使用:0次
解题方法
2 . 已知四棱锥 的底面
的底面 为菱形,其中
为菱形,其中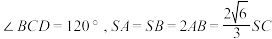 ,点
,点 在线段
在线段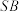 上,若平面
上,若平面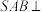 平面
平面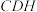 ,则
,则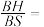
______ .
 的底面
的底面 为菱形,其中
为菱形,其中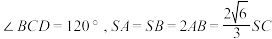 ,点
,点 在线段
在线段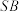 上,若平面
上,若平面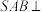 平面
平面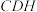 ,则
,则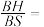
您最近半年使用:0次
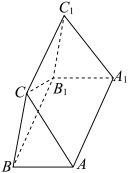
3 . 如图,已知三棱柱 的体积为
的体积为 ,点
,点 在平面
在平面 内的射影落在棱
内的射影落在棱 上,且
上,且 .
. 平面
平面 ;
;
(2)若四边形 的面积为
的面积为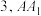 与
与 的距离为
的距离为 ,
, ,求平面
,求平面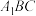 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 的体积为
的体积为 ,点
,点 在平面
在平面 内的射影落在棱
内的射影落在棱 上,且
上,且 .
.
 平面
平面 ;
;(2)若四边形
 的面积为
的面积为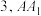 与
与 的距离为
的距离为 ,
, ,求平面
,求平面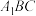 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
您最近半年使用:0次
4 . 如图,在四棱锥 中,
中, 平面
平面 ,
,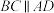 ,
,  ,
, 为
为 的中点.
的中点. 是否为正三角形,并给出证明;
是否为正三角形,并给出证明;
(2)若直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 中,
中, 平面
平面 ,
,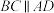 ,
,  ,
, 为
为 的中点.
的中点.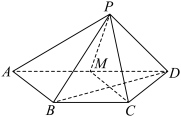
 是否为正三角形,并给出证明;
是否为正三角形,并给出证明;(2)若直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
您最近半年使用:0次
名校
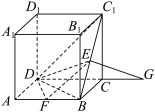
5 . 如图,在正方体 中,
中, 分别为
分别为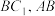 的中点,点
的中点,点 在
在 的延长线上,且
的延长线上,且 .
. 平面
平面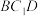 .
.
(2)求平面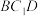 与平面
与平面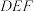 的夹角余弦值.
的夹角余弦值.
 中,
中, 分别为
分别为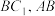 的中点,点
的中点,点 在
在 的延长线上,且
的延长线上,且 .
.
 平面
平面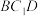 .
.(2)求平面
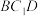 与平面
与平面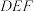 的夹角余弦值.
的夹角余弦值.
您最近半年使用:0次
昨日更新
|
226次组卷
|
3卷引用:湖南省衡阳县三校联考2023-2024学年高二下学期4月月考数学试题
湖南省衡阳县三校联考2023-2024学年高二下学期4月月考数学试题吉林省部分名校(抚松县第一中学等)2023-2024学年高二下学期期中联考数学试卷(已下线)模块一 专题6 《空间向量应用》(苏教版)
6 . 如图,在长方体 中,
中,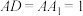 ,
, ,
, 为
为 的中点.
的中点.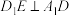 ;
;
(2)求平面 与平面
与平面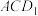 夹角的余弦值.
夹角的余弦值.
 中,
中,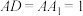 ,
, ,
, 为
为 的中点.
的中点.
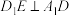 ;
;(2)求平面
 与平面
与平面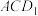 夹角的余弦值.
夹角的余弦值.
您最近半年使用:0次
名校
解题方法
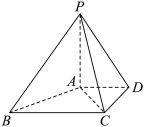
7 . 如图所示,在四棱锥 中,
中, 平面
平面 ,
,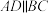 ,
, ,且
,且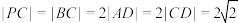 ,
,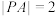 .
.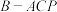 的体积;
的体积;
(2)求证: .
.
 中,
中, 平面
平面 ,
,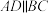 ,
, ,且
,且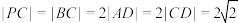 ,
,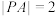 .
.
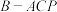 的体积;
的体积;(2)求证:
 .
.
您最近半年使用:0次
8 . 如图,在三棱锥 中,侧面
中,侧面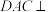 底面
底面 ,
, ,
, .
.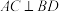 ;
;
(2)已知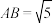 ,
,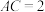 ,
,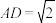 ,
, 是线段
是线段 上一点,当
上一点,当 时,求二面角
时,求二面角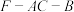 的余弦值.
的余弦值.
 中,侧面
中,侧面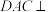 底面
底面 ,
, ,
, .
.
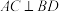 ;
;(2)已知
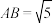 ,
,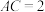 ,
,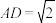 ,
, 是线段
是线段 上一点,当
上一点,当 时,求二面角
时,求二面角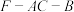 的余弦值.
的余弦值.
您最近半年使用:0次
9 . 如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
, ,
, 分别为
分别为 的中点.
的中点.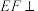 平面
平面 ;
;
(2)设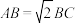 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
, ,
, 分别为
分别为 的中点.
的中点.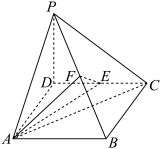
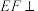 平面
平面 ;
;(2)设
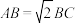 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近半年使用:0次
名校
解题方法
10 . 如图,在矩形ABCD中, ,
,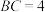 ,M是AD的中点,将
,M是AD的中点,将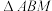 沿着直线BM翻折得到
沿着直线BM翻折得到 .记二面角
.记二面角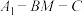 的平面角为
的平面角为 ,当
,当 的值在区间
的值在区间 范围内变化时,下列说法正确的有( )
范围内变化时,下列说法正确的有( )
 ,
,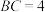 ,M是AD的中点,将
,M是AD的中点,将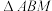 沿着直线BM翻折得到
沿着直线BM翻折得到 .记二面角
.记二面角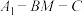 的平面角为
的平面角为 ,当
,当 的值在区间
的值在区间 范围内变化时,下列说法正确的有( )
范围内变化时,下列说法正确的有( )
A.存在 ,使得 ,使得 |
B.存在 ,使得 ,使得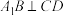 |
C.若四棱锥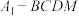 的体积最大时,点B到平面 的体积最大时,点B到平面 的距离为 的距离为 |
D.若直线 与BC所成的角为 与BC所成的角为 ,则 ,则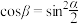 |
您最近半年使用:0次



