解题方法
1 . 已知椭圆 :
: 的离心率为
的离心率为 ,A,B分别是E的左、右顶点,P是E上异于A,B的点,
,A,B分别是E的左、右顶点,P是E上异于A,B的点,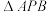 的面积的最大值为
的面积的最大值为 .
.
(1)求E的方程;
(2)设O为原点,点N在直线 上,N,P分别在x轴的两侧,且
上,N,P分别在x轴的两侧,且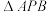 与
与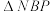 的面积相等.
的面积相等.
(i)求证:直线 与直线
与直线 的斜率之积为定值;
的斜率之积为定值;
(ⅱ)是否存在点P使得 ,若存在,求出点P的坐标,若不存在,说明理由.
,若存在,求出点P的坐标,若不存在,说明理由.
 :
: 的离心率为
的离心率为 ,A,B分别是E的左、右顶点,P是E上异于A,B的点,
,A,B分别是E的左、右顶点,P是E上异于A,B的点,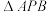 的面积的最大值为
的面积的最大值为 .
.(1)求E的方程;
(2)设O为原点,点N在直线
 上,N,P分别在x轴的两侧,且
上,N,P分别在x轴的两侧,且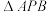 与
与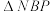 的面积相等.
的面积相等.(i)求证:直线
 与直线
与直线 的斜率之积为定值;
的斜率之积为定值;(ⅱ)是否存在点P使得
 ,若存在,求出点P的坐标,若不存在,说明理由.
,若存在,求出点P的坐标,若不存在,说明理由.
您最近半年使用:0次
解题方法
2 . 已知椭圆 的上顶点为
的上顶点为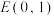 ,且经过点
,且经过点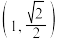 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过点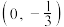 且斜率存在的直线与椭圆
且斜率存在的直线与椭圆 交于
交于 两点,判断
两点,判断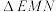 的形状并给出证明.
的形状并给出证明.
 的上顶点为
的上顶点为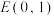 ,且经过点
,且经过点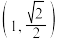 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
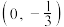 且斜率存在的直线与椭圆
且斜率存在的直线与椭圆 交于
交于 两点,判断
两点,判断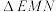 的形状并给出证明.
的形状并给出证明.
您最近半年使用:0次
解题方法
3 . 已知椭圆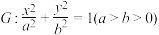 的一个顶点为
的一个顶点为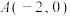 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)设 为原点.直线
为原点.直线 与椭圆
与椭圆 交于
交于 两点(
两点( 不是椭圆的顶点),
不是椭圆的顶点), 与直线
与直线 交于点
交于点 ,直线
,直线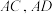 分别与直线
分别与直线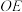 交于点
交于点 .求证:
.求证: .
.
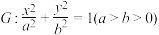 的一个顶点为
的一个顶点为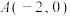 ,离心率为
,离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)设
 为原点.直线
为原点.直线 与椭圆
与椭圆 交于
交于 两点(
两点( 不是椭圆的顶点),
不是椭圆的顶点), 与直线
与直线 交于点
交于点 ,直线
,直线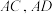 分别与直线
分别与直线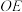 交于点
交于点 .求证:
.求证: .
.
您最近半年使用:0次
名校
解题方法
4 . 已知椭圆C: 的焦距是短轴长的
的焦距是短轴长的 倍,以椭圆的四个顶点为顶点的四边形周长为
倍,以椭圆的四个顶点为顶点的四边形周长为 .
.
(1)求椭圆的方程;
(2)直线 与椭圆C交于A、B两点,与y轴交于点P,线段AB的垂直平分线与AB交于点M,与y轴交于点N,O为坐标原点,如果
与椭圆C交于A、B两点,与y轴交于点P,线段AB的垂直平分线与AB交于点M,与y轴交于点N,O为坐标原点,如果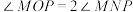 ,求k的值.
,求k的值.
 的焦距是短轴长的
的焦距是短轴长的 倍,以椭圆的四个顶点为顶点的四边形周长为
倍,以椭圆的四个顶点为顶点的四边形周长为 .
.(1)求椭圆的方程;
(2)直线
 与椭圆C交于A、B两点,与y轴交于点P,线段AB的垂直平分线与AB交于点M,与y轴交于点N,O为坐标原点,如果
与椭圆C交于A、B两点,与y轴交于点P,线段AB的垂直平分线与AB交于点M,与y轴交于点N,O为坐标原点,如果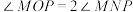 ,求k的值.
,求k的值.
您最近半年使用:0次
解题方法
5 . 已知椭圆 的离心率为
的离心率为 ,短轴长为
,短轴长为 .
.
(1)求椭圆 的方程;
的方程;
(2)设 为坐标原点,过点
为坐标原点,过点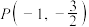 分别作直线
分别作直线 ,直线
,直线 与椭圆相切于第三象限内的点
与椭圆相切于第三象限内的点 ,直线
,直线 交椭圆
交椭圆 于
于 两点.若
两点.若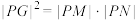 ,判断直线
,判断直线 与直线
与直线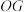 的位置关系,并说明理由.
的位置关系,并说明理由.
 的离心率为
的离心率为 ,短轴长为
,短轴长为 .
.(1)求椭圆
 的方程;
的方程;(2)设
 为坐标原点,过点
为坐标原点,过点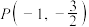 分别作直线
分别作直线 ,直线
,直线 与椭圆相切于第三象限内的点
与椭圆相切于第三象限内的点 ,直线
,直线 交椭圆
交椭圆 于
于 两点.若
两点.若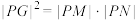 ,判断直线
,判断直线 与直线
与直线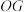 的位置关系,并说明理由.
的位置关系,并说明理由.
您最近半年使用:0次
解题方法
6 . 已知椭圆 的离心率为
的离心率为 ,短轴长为
,短轴长为 .
.
(1)求椭圆C的标准方程;
(2)已知点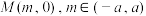 ,过点M且斜率不为0的直线l交椭圆于P,Q两点,当
,过点M且斜率不为0的直线l交椭圆于P,Q两点,当 时,求m的值.
时,求m的值.
 的离心率为
的离心率为 ,短轴长为
,短轴长为 .
.(1)求椭圆C的标准方程;
(2)已知点
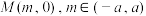 ,过点M且斜率不为0的直线l交椭圆于P,Q两点,当
,过点M且斜率不为0的直线l交椭圆于P,Q两点,当 时,求m的值.
时,求m的值.
您最近半年使用:0次
解题方法
7 . 已知椭圆 的上顶点为
的上顶点为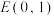 ,且经过点
,且经过点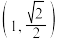 .
.
(1)求 的标准方程;
的标准方程;
(2)过点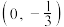 的直线与
的直线与 交于
交于 ,
, 两点,判断
两点,判断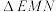 的形状并给出证明.
的形状并给出证明.
 的上顶点为
的上顶点为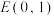 ,且经过点
,且经过点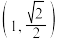 .
.(1)求
 的标准方程;
的标准方程;(2)过点
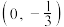 的直线与
的直线与 交于
交于 ,
, 两点,判断
两点,判断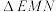 的形状并给出证明.
的形状并给出证明.
您最近半年使用:0次
解题方法
8 . 已知椭圆的焦点分别是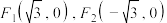 ,点
,点 在椭圆上,且
在椭圆上,且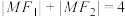 .
.
(1)求椭圆的标准方程;
(2)若直线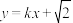 与椭圆交于
与椭圆交于 两点,且
两点,且 ,求实数
,求实数 的值.
的值.
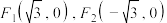 ,点
,点 在椭圆上,且
在椭圆上,且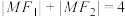 .
.(1)求椭圆的标准方程;
(2)若直线
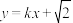 与椭圆交于
与椭圆交于 两点,且
两点,且 ,求实数
,求实数 的值.
的值.
您最近半年使用:0次
名校
解题方法
9 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,上、下顶点分别为
,上、下顶点分别为 ,且
,且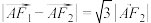 ,
,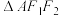 的面积为
的面积为 .
.
(1)求 的方程;
的方程;
(2)已知 为直线
为直线 上任一点,设直线
上任一点,设直线 与
与 的另一个公共点分别为
的另一个公共点分别为 .问:直线
.问:直线 是否过一定点?若过定点,求出该定点的坐标;若不过定点,试说明理由.
是否过一定点?若过定点,求出该定点的坐标;若不过定点,试说明理由.
 的左、右焦点分别为
的左、右焦点分别为 ,上、下顶点分别为
,上、下顶点分别为 ,且
,且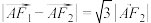 ,
,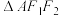 的面积为
的面积为 .
.(1)求
 的方程;
的方程;(2)已知
 为直线
为直线 上任一点,设直线
上任一点,设直线 与
与 的另一个公共点分别为
的另一个公共点分别为 .问:直线
.问:直线 是否过一定点?若过定点,求出该定点的坐标;若不过定点,试说明理由.
是否过一定点?若过定点,求出该定点的坐标;若不过定点,试说明理由.
您最近半年使用:0次
2024-04-17更新
|
232次组卷
|
2卷引用:宁夏固原市第一中学2024届高三下学期模拟考试文科数学试题(一)
解题方法
10 . 已知椭圆 的左焦点为F,P,Q分别为左顶点和上顶点,O为坐标原点,
的左焦点为F,P,Q分别为左顶点和上顶点,O为坐标原点, (
( 为椭圆的离心率),
为椭圆的离心率), 的面积为
的面积为 .
.
(1)求椭圆 的方程;
的方程;
(2)直线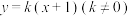 与椭圆交于
与椭圆交于 两点,过
两点,过 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为 、
、 ,点
,点 为线段
为线段 的中点.求证:四边形
的中点.求证:四边形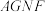 为梯形.
为梯形.
 的左焦点为F,P,Q分别为左顶点和上顶点,O为坐标原点,
的左焦点为F,P,Q分别为左顶点和上顶点,O为坐标原点, (
( 为椭圆的离心率),
为椭圆的离心率), 的面积为
的面积为 .
.(1)求椭圆
 的方程;
的方程;(2)直线
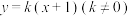 与椭圆交于
与椭圆交于 两点,过
两点,过 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为 、
、 ,点
,点 为线段
为线段 的中点.求证:四边形
的中点.求证:四边形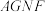 为梯形.
为梯形.
您最近半年使用:0次



