1 . 某地文化和旅游局统计了春节期间100个家庭的旅游支出情况，统计得到这100个家庭的旅游支出（单位：千元）数据，按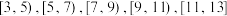
分成5组，并绘制成频率分布直方图，如图所示．
(2)估计这100个家庭的旅游支出的第70百分位数（结果保留一位小数）；
(3)以这100个家庭的旅游支出数据各组的频率代替各组的概率，在全国范围内随机抽取2个春节期间出游的家庭，每个家庭的旅游支出情况互相不受影响，求恰有1个家庭的旅游支出在
内的概率．
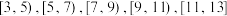分成5组，并绘制成频率分布直方图，如图所示．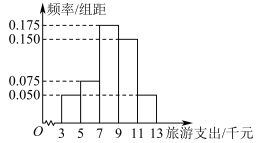
(2)估计这100个家庭的旅游支出的第70百分位数（结果保留一位小数）；
(3)以这100个家庭的旅游支出数据各组的频率代替各组的概率，在全国范围内随机抽取2个春节期间出游的家庭，每个家庭的旅游支出情况互相不受影响，求恰有1个家庭的旅游支出在
内的概率．
您最近半年使用：0次
昨日更新
|
386次组卷
|
5卷引用：江西省部分高中学校2023-2024学年高一下学期联考数学试卷
江西省部分高中学校2023-2024学年高一下学期联考数学试卷贵州省遵义市遵义市四城区联考2023-2024学年高一下学期4月月考数学试题（已下线）专题10.6 概率全章八大压轴题型归纳（拔尖篇-举一反三系列（人教A版2019必修第二册）（已下线）专题10.2 事件的相互独立性-举一反三系列（人教A版2019必修第二册）（已下线）10.2?事件的相互独立性——随堂检测
2024·全国·模拟预测
解题方法
2 . 中央广播电视总台《2024年春节联欢晚会》以“龙行龘龘，欣欣家国”为主题，创新“思想
艺术技术”融合传播，与全球华人相约除夕，共享一台精彩纷呈、情真意切、热气腾腾的文化盛宴.2023年12月2日，中央广播电视总台发布了甲辰龙年春晚的主标识——龘．为了解大家对这一标识的看法，某网站进行了一次网络调研，并将参与调查的网友对这一标识的打分情况（分数在50分到100分之间）绘制成频率分布直方图如下：
(2)设网友打分的平均值为
，若按打分是否在区间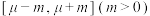
内进行分层抽样，抽取10人进行深度调研，打分在区间
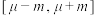内的至少抽取8人，试估计
的最小值（保留两位小数）．
艺术技术”融合传播，与全球华人相约除夕，共享一台精彩纷呈、情真意切、热气腾腾的文化盛宴.2023年12月2日，中央广播电视总台发布了甲辰龙年春晚的主标识——龘．为了解大家对这一标识的看法，某网站进行了一次网络调研，并将参与调查的网友对这一标识的打分情况（分数在50分到100分之间）绘制成频率分布直方图如下：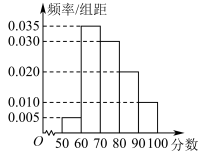
(2)设网友打分的平均值为
，若按打分是否在区间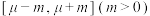内进行分层抽样，抽取10人进行深度调研，打分在区间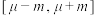内的至少抽取8人，试估计的最小值（保留两位小数）．
您最近半年使用：0次
解题方法
3 . 在某市高三年级等行的一次数学期末考试中，为了解考生的成绩情况，随机抽取了50名考生的成绩，作出的频率分布直方图如图，成绩排在前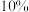
的学生将获得“优秀学生”称号，则（ ）
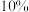的学生将获得“优秀学生”称号，则（ ）
A．估计该市考生的成绩低于60分的比例为 |
| B．估计该市考生成绩的众数为60 |
| C．估计该市考生成绩的平均数为70.6 |
| D．估计该市82分以上的考生将获得“优秀学生”称号 |
您最近半年使用：0次
解题方法
4 . 某教育机构为调查中小学生每日完成作业的时间，收集了某位学生100天每天完成作业的时间，并绘制了如图所示的频率分布直方图（每个区间均为左闭右开），根据此直方图得出了下列结论，其中正确的是（ ）
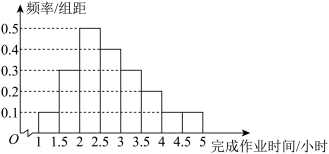
| A．估计该学生每日完成作业的时间在2小时至2.5小时的有50天 |
| B．估计该学生每日完成作业时间超过3小时的概率为0.3 |
| C．估计该学生每日完成作业时间的平均数为2.75小时 |
| D．估计该学生每日完成作业时间的中位数与平均数相等 |
您最近半年使用：0次
名校
解题方法
5 . 在某次学科期末检测后，从全部考生中选取100名考生的成绩（百分制，均为整数）分成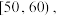
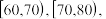
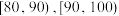五组后，得到频率分布直方图（如右图），则下列说法正确的是（ ）
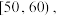
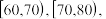
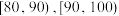五组后，得到频率分布直方图（如右图），则下列说法正确的是（ ）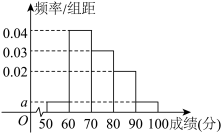
A．图中 的值为0.005 | B．低于70分的考生人数约为40人 |
| C．考生成绩的平均分约为73分 | D．估计考生成绩第80百分位数为82.5分 |
您最近半年使用：0次
6 . 为促进物资流通，改善出行条件，驻某县扶贫工作组引入资金新建了一条从该县到市区的快速道路．该县脱贫后，工作组为了解该快速道路的交通通行状况，调查了行经该道路的各种类别的机动车共1000辆，对行车速度进行统计后，得到如图所示的频率分布直方图：的值以及样本中的这1000辆机动车的平均车速（同一组中的数据用该组区间的中点值代替）；
(2)设该公路上机动车的行车速度服从正态分布
，其中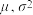
分别取自该调查样本中机动车的平均车速和车速的方差
（经计算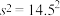
）．
（i）请估计该公路上10000辆机动车中车速不低于85千米/时的车辆数（精确到个位）；
（ii）现从经过该公路的机动车中随机抽取10辆，设车速低于85千米/时的车辆数为
，求的数学期望．
附注：若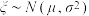
，则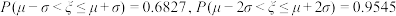
，
．
的值以及样本中的这1000辆机动车的平均车速（同一组中的数据用该组区间的中点值代替）；(2)设该公路上机动车的行车速度服从正态分布
，其中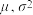分别取自该调查样本中机动车的平均车速和车速的方差（经计算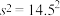）．（i）请估计该公路上10000辆机动车中车速不低于85千米/时的车辆数（精确到个位）；
（ii）现从经过该公路的机动车中随机抽取10辆，设车速低于85千米/时的车辆数为
，求的数学期望．附注：若
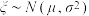，则，．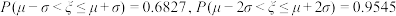
您最近半年使用：0次
2024高一下·全国·专题练习
解题方法
7 . 文明城市是反映城市整体文明水平的综合性荣誉称号，作为普通市民，既是文明城市的最大受益者，更是文明城市的主要创造者.某市为提高市民对文明城市创建的认识，举办了“创建文明城市”知识竞赛，从所有答卷中随机抽取100份作为样本，将样本的成绩（满分100分，成绩均为不低于40分的整数）分成六段：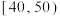
，
，
，
得到如图所示的频率分布直方图.的值；
(2)求样本成绩的第75百分位数；
(3)已知落在的平均成绩是61，方差是7，落在
的平均成绩为70，方差是4，求两组成绩的总平均数
和总方差.
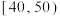，，，得到如图所示的频率分布直方图.
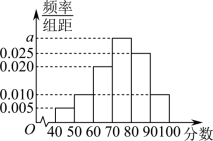
的值；(2)求样本成绩的第75百分位数；
(3)已知落在
的平均成绩是61，方差是7，落在的平均成绩为70，方差是4，求两组成绩的总平均数和总方差.
您最近半年使用：0次
解题方法
8 . 某中学为了解大数据提供的个性化作业质量情况，随机访问
名学生，并对这名学生的个性化作业进行评分（满分：100分），根据得分将他们的成绩分成
，
，
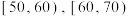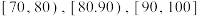六组，制成如图所示的频率分布直方图，其中成绩在
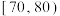的学生人数为30人．
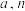的值；
(2)估计这名学生成绩的平均数（同一组数据用该组数据的中点值代替）和中位数．
名学生，并对这名学生的个性化作业进行评分（满分：100分），根据得分将他们的成绩分成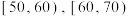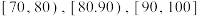，，六组，制成如图所示的频率分布直方图，其中成绩在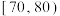的学生人数为30人．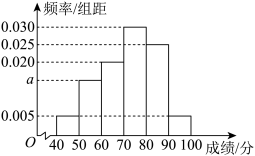
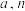的值；(2)估计这
名学生成绩的平均数（同一组数据用该组数据的中点值代替）和中位数．
您最近半年使用：0次
名校
解题方法
9 . 某社区通过简单随机抽样，获得了100户居民的月均用水量数据，并绘制出如图所示的频率分布直方图，由该图可以估计（ ）
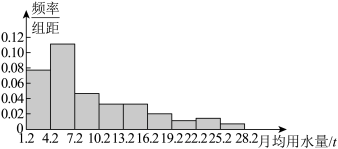
| A．平均数>中位数 | B．中位数>平均数 |
| C．中位数>众数 | D．众数>平均数 |
您最近半年使用：0次
7日内更新
|
259次组卷
|
3卷引用：重庆市第八中学2024届高三下学期3月适应性月考卷（六）数学试题
名校
解题方法
10 . 下图是样本甲与样本乙的频率分布直方图，下列说法判断正确的是（ ）
| A．样本乙的极差一定大于样本甲的极差 |
| B．样本乙的众数一定大于样本甲的众数 |
| C．样本甲的方差一定大于样本乙的方差 |
| D．样本甲的中位数一定小于样本乙的中位数 |
您最近半年使用：0次
7日内更新
|
581次组卷
|
4卷引用：辽宁省协作校2024届高三下学期第一次模拟考试数学试题
辽宁省协作校2024届高三下学期第一次模拟考试数学试题（已下线）专题9.6 统计全章综合测试卷（基础篇）--举一反三系列（人教A版2019必修第二册）2024届广东省高三毕业班综合能力测试（华娇教育摸底测试）数学试题 （已下线）9.2.4?总体离散程度的估计——课后作业（巩固版）
