1 . 长跑可提高呼吸系统和心血管系统机能,较长时间有节奏的深长呼吸,能使人体呼吸大量的氧气,吸收氧气量若超过平时的7—8倍,就可以抑制人体癌细胞的生长和繁殖.其次长跑锻炼还改善了心肌供氧状态,加快了心肌代谢,同时还使心肌肌纤维变粗,心收缩力增强,从而提高了心脏工作能力.某学校对男、女学生是否喜欢长跑进行了调查,调查男、女生人数均为200,统计得到以下 列联表:
列联表:
(1)试根据小概率值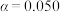 的独立性检验,能否认为学生对长跑的喜欢情况与性别有关联?
的独立性检验,能否认为学生对长跑的喜欢情况与性别有关联?
(2)为弄清学生不喜欢长跑的原因,从调查的不喜欢长跑的学生中按性别采用分层抽样的方法随机抽取9人,再从这9人中抽取3人进行面对面交流,记随机变量X表示抽到的3人中女生的人数,求X的分布列;
(3)将频率视为概率,用样本估计总体,从该校全体学生中随机抽取12人,记其中喜欢长跑的人数为Y,求Y的数学期望.
附: ,其中
,其中 .
.
 列联表:
列联表:喜欢 | 不喜欢 | 合计 | |
男生 | 120 | 80 | 200 |
女生 | 100 | 100 | 200 |
合计 | 220 | 180 | 400 |
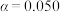 的独立性检验,能否认为学生对长跑的喜欢情况与性别有关联?
的独立性检验,能否认为学生对长跑的喜欢情况与性别有关联?(2)为弄清学生不喜欢长跑的原因,从调查的不喜欢长跑的学生中按性别采用分层抽样的方法随机抽取9人,再从这9人中抽取3人进行面对面交流,记随机变量X表示抽到的3人中女生的人数,求X的分布列;
(3)将频率视为概率,用样本估计总体,从该校全体学生中随机抽取12人,记其中喜欢长跑的人数为Y,求Y的数学期望.
附:
 ,其中
,其中 .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
您最近半年使用:0次
解题方法
2 . 某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.完成生产任务的工作时间不超过70分钟的工人为“优秀”,否则为“合格”.根据工人完成生产任务的工作时间(单位:分钟)绘制了如下茎叶图:
(2)独立地从两种生产方式中各选出一个人,求选出的两个人均为优秀的概率;
(3)根据工人完成生产任务的工作时间,两种生产方式优秀与合格的人数填入下面的2×2列联表:
根据上面的2×2列联表,判断能否有95%的把握认为两种生产方式的工作效率有显著差异?( .其中
.其中 ,
,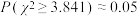 ).
).
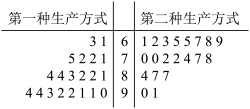
(2)独立地从两种生产方式中各选出一个人,求选出的两个人均为优秀的概率;
(3)根据工人完成生产任务的工作时间,两种生产方式优秀与合格的人数填入下面的2×2列联表:
第一种生产方式 | 第二种生产方式 | 总计 | |
优秀 | |||
合格 | |||
总计 |
 .其中
.其中 ,
,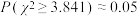 ).
).
您最近半年使用:0次
3 . 某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
(1)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(2)若某天的空气质量等级为 或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的
或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的 列联表,请根据表中的数据判断:一天中到该公园锻炼的人次是否与该市当天的空气质量有关?(规定显著性水平
列联表,请根据表中的数据判断:一天中到该公园锻炼的人次是否与该市当天的空气质量有关?(规定显著性水平 )
)
附: ,
, .
.
锻炼人次 空气质量等级 | 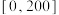 | 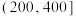 |  |
| 1(优) | 3 | 18 | 25 |
| 2(良) | 6 |  | 14 |
| 3(轻度污染) | 5 | 5 | 6 |
| 4(中度污染) | 6 | 3 | 0 |
(2)若某天的空气质量等级为
 或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的
或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的 列联表,请根据表中的数据判断:一天中到该公园锻炼的人次是否与该市当天的空气质量有关?(规定显著性水平
列联表,请根据表中的数据判断:一天中到该公园锻炼的人次是否与该市当天的空气质量有关?(规定显著性水平 )
)| 人次≤400 | 人次>400 | 总计 | |
| 空气质量好 | |||
| 空气质量不好 | |||
| 总计 |
 ,
, .
.
您最近半年使用:0次
解题方法
4 . 某疾病预防中心随机调查了339名50岁以上的公民,研究吸烟习惯与慢性气管炎患病的关系,调查数据如下表:
假设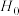 :患慢性气管炎与吸烟没有关系,即它们相互独立.通过计算统计量
:患慢性气管炎与吸烟没有关系,即它们相互独立.通过计算统计量 ,得
,得 ,根据
,根据 分布概率表:
分布概率表: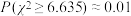 ,
,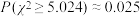 ,
,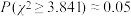 ,
, .给出下列3个命题,其中正确的个数是( )
.给出下列3个命题,其中正确的个数是( )
①“患慢性气管炎与吸烟没有关系”成立的可能性小于 ;
;
②有 的把握认为患慢性气管炎与吸烟有关;
的把握认为患慢性气管炎与吸烟有关;
③ 分布概率表中的
分布概率表中的 、
、 等小概率值在统计上称为显著性水平,小概率事件一般认为不太可能发生.
等小概率值在统计上称为显著性水平,小概率事件一般认为不太可能发生.
| 不吸烟者 | 吸烟者 | 总计 | |
| 不患慢性气管炎者 | 121 | 162 | 283 |
| 患慢性气管炎者 | 13 | 43 | 56 |
| 总计 | 134 | 205 | 339 |
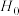 :患慢性气管炎与吸烟没有关系,即它们相互独立.通过计算统计量
:患慢性气管炎与吸烟没有关系,即它们相互独立.通过计算统计量 ,得
,得 ,根据
,根据 分布概率表:
分布概率表: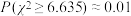 ,
,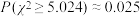 ,
,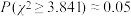 ,
, .给出下列3个命题,其中正确的个数是( )
.给出下列3个命题,其中正确的个数是( )①“患慢性气管炎与吸烟没有关系”成立的可能性小于
 ;
;②有
 的把握认为患慢性气管炎与吸烟有关;
的把握认为患慢性气管炎与吸烟有关;③
 分布概率表中的
分布概率表中的 、
、 等小概率值在统计上称为显著性水平,小概率事件一般认为不太可能发生.
等小概率值在统计上称为显著性水平,小概率事件一般认为不太可能发生.A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
您最近半年使用:0次
5 . 已知甲社区有120人计划去四川旅游,他们每人将从峨眉山与青城山中选择一个去旅游,将这120人分为东、西两小组,两组的人数相等,已知东小组中去峨眉山的人数是去青城山人数的两倍,西小组中去峨眉山的人数比去青城山的人数少10.
(1)完成下面的 列联表,并判断是否有99%的把握认为游客的选择与所在的小组有关;
列联表,并判断是否有99%的把握认为游客的选择与所在的小组有关;
(2)在东小组的游客中,以他们去青城山旅游的频率为乙社区游客去青城山旅游的概率,从乙社区任选3名游客,记这3名游客中去青城山旅游的人数为X,求 及X的数学期望.
及X的数学期望.
参考公式: ,
, .
.
(1)完成下面的
 列联表,并判断是否有99%的把握认为游客的选择与所在的小组有关;
列联表,并判断是否有99%的把握认为游客的选择与所在的小组有关;去峨眉山旅游 | 去青城山旅游 | 合计 | |
东小组 | |||
西小组 | |||
合计 |
 及X的数学期望.
及X的数学期望.参考公式:
 ,
, .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
2024·全国·模拟预测
6 . 某校组织了科技展参观活动,学生自愿参观,事后学校进行了一次问卷调查,分别抽取男、女生各40人作为样本.据统计:男生参观科技展的概率为 ,参观科技展的学生中女生占
,参观科技展的学生中女生占 .
.
(1)根据已知条件,填写下列 列联表,试根据小概率值
列联表,试根据小概率值 的独立性检验,分析该校学生参观科技展情况与性别是否有关.
的独立性检验,分析该校学生参观科技展情况与性别是否有关.
(2)用分层随机抽样的方式从参观科技展的人中抽取12人,再从这12人中随机抽取6人,用随机变量 表示女生人数,求
表示女生人数,求 的分布列和数学期望.
的分布列和数学期望.
参考公式和数据: ,其中
,其中 .
.
 ,参观科技展的学生中女生占
,参观科技展的学生中女生占 .
.(1)根据已知条件,填写下列
 列联表,试根据小概率值
列联表,试根据小概率值 的独立性检验,分析该校学生参观科技展情况与性别是否有关.
的独立性检验,分析该校学生参观科技展情况与性别是否有关.| 参观科技展 | 未参观科技展 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
 表示女生人数,求
表示女生人数,求 的分布列和数学期望.
的分布列和数学期望.参考公式和数据:
 ,其中
,其中 .
. | 0.1 | 0.05 | 0.025 | 0.01 | 0.001 |
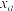 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
您最近半年使用:0次
名校
7 . 2024年3月,某校语文教师对学生提出“3月读一本书”的要求,每位学生都选择且只能选择《红楼梦》和《三国演义》中的一本,现随机调查该校男、女生各100人,发现选择《红楼梦》的有90人,其中女生占 .
.
(1)补充完整下述 列联表,并判断能否有
列联表,并判断能否有 的把握认为学生选择《红楼梦》还是《三国演义》与性别有关;
的把握认为学生选择《红楼梦》还是《三国演义》与性别有关;
(2)已知学生选择哪本书是相互独立的,用频率代替概率,从该校选择《红楼梦》的学生中随机抽取3人,抽到的女生人数设为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式: ,其中
,其中 .
.
参考数据:
 .
.(1)补充完整下述
 列联表,并判断能否有
列联表,并判断能否有 的把握认为学生选择《红楼梦》还是《三国演义》与性别有关;
的把握认为学生选择《红楼梦》还是《三国演义》与性别有关;| 《红楼梦》 | 《三国演义》 | |
| 男生 | ||
| 女生 |
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.参考公式:
 ,其中
,其中 .
.参考数据:
 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
昨日更新
|
196次组卷
|
2卷引用:陕西省安康市高新中学、安康中学高新分校2023-2024学年高三阶段性测试(八)理科数学试题
8 . 近期一个被网友戏称为“科目三”的魔性舞蹈横空出世,欢快的场景、强烈的节奏加上夸张、土味的肢体动作,成为年轻人争相模仿学习的舞蹈新宠.然而任何事物都有其两面性,丝滑魔性的舞蹈动作在吸引人模仿的同时,脚踝的循环内翻、外翻这个动作,如果平衡节奏把握不当,就容易引起脚踝处的损伤:为了解小学生是否知道“科目三”舞蹈会带来损伤,志愿者随机走访了90名小学生,得到相关数据如下:
(1)根据统计数据,依据小概率值 的独立性检验,分析“知道‘科目三’舞蹈会带来损伤”与“学生的年龄段”是否有关;
的独立性检验,分析“知道‘科目三’舞蹈会带来损伤”与“学生的年龄段”是否有关;
(2)为了解小学生们对待新鲜事物的态度,按低年龄段、高年龄段进行分层,用分层随机抽样的方式从上述走访的知道“科目三”舞蹈会带来损伤的学生中邀请了7名学生,从这7名学生中随机抽取3名填写调查表,记X为这3名学生中为高年龄段的人数,求X的分布列和数学期望.
附表及公式:
 ,其中
,其中 .
.
知道 | 不知道 | 总计 | |
低年龄段 | 14 | 26 | 40 |
高年龄段 | 35 | 15 | 50 |
总计 | 49 | 41 | 90 |
(1)根据统计数据,依据小概率值
 的独立性检验,分析“知道‘科目三’舞蹈会带来损伤”与“学生的年龄段”是否有关;
的独立性检验,分析“知道‘科目三’舞蹈会带来损伤”与“学生的年龄段”是否有关;(2)为了解小学生们对待新鲜事物的态度,按低年龄段、高年龄段进行分层,用分层随机抽样的方式从上述走访的知道“科目三”舞蹈会带来损伤的学生中邀请了7名学生,从这7名学生中随机抽取3名填写调查表,记X为这3名学生中为高年龄段的人数,求X的分布列和数学期望.
附表及公式:
| 0.1 | 0.05 | 0.01 | 0.05 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 .
.
您最近半年使用:0次
2024·全国·模拟预测
解题方法
9 . 冬季是某种流行疾病的高发季,为了检测预防这种疾病疫苗的免疫效果,对200名志愿者注射该疫苗,一段时间后,统计了这200名志愿者的年龄 (单位:岁),并测量他们血液中的抗体医学指标
(单位:岁),并测量他们血液中的抗体医学指标 .现作出
.现作出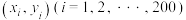 的散点图,如下:
的散点图,如下: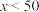 岁的志愿者中抗体医学指标
岁的志愿者中抗体医学指标 的有64人,
的有64人, 的有24人;年龄
的有24人;年龄 岁的志愿者中抗体医学指标
岁的志愿者中抗体医学指标 的有32人,
的有32人, 的有80人.
的有80人.
(1)请完成下面的 列联表,并根据小概率值
列联表,并根据小概率值 的独立性检验,判断能否认为抗体医学指标不小于80与年龄不小于50岁有关.
的独立性检验,判断能否认为抗体医学指标不小于80与年龄不小于50岁有关.
(2)对数据初步处理后计算得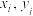 的方差分别为40.5,162,
的方差分别为40.5,162, 关于
关于 的经验回归方程为
的经验回归方程为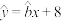 ,且其样本相关系数
,且其样本相关系数 ,求
,求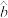 的值.若一名65岁的志愿者注射该疫苗,经过和200名志愿者注射后相同长度的一段时间后,预测这名志愿者的抗体医学指标值.
的值.若一名65岁的志愿者注射该疫苗,经过和200名志愿者注射后相同长度的一段时间后,预测这名志愿者的抗体医学指标值.
参考公式: (其中
(其中 ).
).
经验回归方程为 ,其中
,其中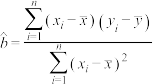 ,变量
,变量 与变量
与变量 的样本相关系数
的样本相关系数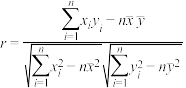 .
.
 (单位:岁),并测量他们血液中的抗体医学指标
(单位:岁),并测量他们血液中的抗体医学指标 .现作出
.现作出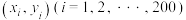 的散点图,如下:
的散点图,如下:
 岁的志愿者中抗体医学指标
岁的志愿者中抗体医学指标 的有64人,
的有64人, 的有24人;年龄
的有24人;年龄 岁的志愿者中抗体医学指标
岁的志愿者中抗体医学指标 的有32人,
的有32人, 的有80人.
的有80人.(1)请完成下面的
 列联表,并根据小概率值
列联表,并根据小概率值 的独立性检验,判断能否认为抗体医学指标不小于80与年龄不小于50岁有关.
的独立性检验,判断能否认为抗体医学指标不小于80与年龄不小于50岁有关.抗体医学指标 | 年龄 | 合计 | |
|
| ||
| |||
| |||
合计 | |||
(2)对数据初步处理后计算得
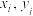 的方差分别为40.5,162,
的方差分别为40.5,162, 关于
关于 的经验回归方程为
的经验回归方程为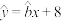 ,且其样本相关系数
,且其样本相关系数 ,求
,求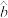 的值.若一名65岁的志愿者注射该疫苗,经过和200名志愿者注射后相同长度的一段时间后,预测这名志愿者的抗体医学指标值.
的值.若一名65岁的志愿者注射该疫苗,经过和200名志愿者注射后相同长度的一段时间后,预测这名志愿者的抗体医学指标值.参考公式:
 (其中
(其中 ).
).
| 0.1 | 0.01 | 0.005 | 0.001 |
| 2.706 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中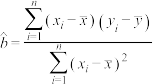 ,变量
,变量 与变量
与变量 的样本相关系数
的样本相关系数 .
.
您最近半年使用:0次
2024·全国·模拟预测
解题方法
10 . 某果农为了解施农家肥与化肥对苹果的大小是否有影响,现将自己所种植的苹果地合理分成两块,并对 地连续施用三年农家肥,对
地连续施用三年农家肥,对 地连续施用三年化肥.在第三年苹果采摘后,分别从
地连续施用三年化肥.在第三年苹果采摘后,分别从 两地的苹果中各抽取200个进行测量,其中
两地的苹果中各抽取200个进行测量,其中 地的大果(
地的大果(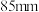 以上)为50个,中果
以上)为50个,中果 为110个,小果(
为110个,小果( 以下)为40个;
以下)为40个; 地的大果为40个,中果为110个,小果为50个.
地的大果为40个,中果为110个,小果为50个.
(1)根据以上数据,补全以下列联表,试根据小概率值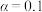 的独立性检验,分析施肥的不同对苹果树结小果数是否有影响.
的独立性检验,分析施肥的不同对苹果树结小果数是否有影响.
(2)现有苹果客商收购苹果,大果价格8元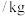 ,中果6.5元
,中果6.5元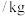 ,小果3元
,小果3元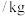 .客商对该果农的苹果质量进行评估:大果约
.客商对该果农的苹果质量进行评估:大果约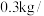 个,中果约
个,中果约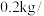 个,小果约
个,小果约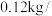 个.假设
个.假设 两地的果树数之比为
两地的果树数之比为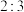 ,且每棵果树结果数相等.该客商为节约时间,对该果农的苹果统一定价为6.5元
,且每棵果树结果数相等.该客商为节约时间,对该果农的苹果统一定价为6.5元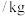 .视频率为概率,用样本估计总体,请你为该果农出主意是否接受客商所给的价格,并给出解释.
.视频率为概率,用样本估计总体,请你为该果农出主意是否接受客商所给的价格,并给出解释.
参考公式及参考数据: ,其中
,其中 .
.
 地连续施用三年农家肥,对
地连续施用三年农家肥,对 地连续施用三年化肥.在第三年苹果采摘后,分别从
地连续施用三年化肥.在第三年苹果采摘后,分别从 两地的苹果中各抽取200个进行测量,其中
两地的苹果中各抽取200个进行测量,其中 地的大果(
地的大果(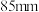 以上)为50个,中果
以上)为50个,中果 为110个,小果(
为110个,小果( 以下)为40个;
以下)为40个; 地的大果为40个,中果为110个,小果为50个.
地的大果为40个,中果为110个,小果为50个.(1)根据以上数据,补全以下列联表,试根据小概率值
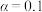 的独立性检验,分析施肥的不同对苹果树结小果数是否有影响.
的独立性检验,分析施肥的不同对苹果树结小果数是否有影响.| 苹果地 | 大小情况 | 合计 | |
| 非小果 | 小果 | ||
 地 地 | |||
 地 地 | |||
| 合计 | |||
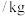 ,中果6.5元
,中果6.5元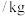 ,小果3元
,小果3元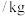 .客商对该果农的苹果质量进行评估:大果约
.客商对该果农的苹果质量进行评估:大果约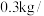 个,中果约
个,中果约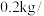 个,小果约
个,小果约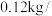 个.假设
个.假设 两地的果树数之比为
两地的果树数之比为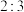 ,且每棵果树结果数相等.该客商为节约时间,对该果农的苹果统一定价为6.5元
,且每棵果树结果数相等.该客商为节约时间,对该果农的苹果统一定价为6.5元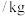 .视频率为概率,用样本估计总体,请你为该果农出主意是否接受客商所给的价格,并给出解释.
.视频率为概率,用样本估计总体,请你为该果农出主意是否接受客商所给的价格,并给出解释.参考公式及参考数据:
 ,其中
,其中 .
. | 0.100 | 0.050 | 0.010 | 0.005 |
 | 2.706 | 3.841 | 6.635 | 7.879 |
您最近半年使用:0次



