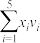解题方法
1 . 某学校工会组织趣味投篮比赛,每名选手只能在下列两种比赛方式中选择一种.
方式一:选手投篮3次,每次投中可得1分,未投中不得分,累计得分;
方式二:选手最多投3次.如第1次投中可进行第2次投篮,如第2次投中可进行第3次投篮.如某次未投中,则投篮中止.每投中1次可得2分,未投中不得分,累计得分;
已知甲选择方式一参加比赛,乙选择方式二参加比赛.假设甲,乙每次投中的概率均为 ,且每次投篮相互独立.
,且每次投篮相互独立.
(1)求甲得分不低于2分的概率;
(2)求乙得分的分布列及期望;
(3)甲,乙谁胜出的可能性更大?直接写出结论.
方式一:选手投篮3次,每次投中可得1分,未投中不得分,累计得分;
方式二:选手最多投3次.如第1次投中可进行第2次投篮,如第2次投中可进行第3次投篮.如某次未投中,则投篮中止.每投中1次可得2分,未投中不得分,累计得分;
已知甲选择方式一参加比赛,乙选择方式二参加比赛.假设甲,乙每次投中的概率均为
 ,且每次投篮相互独立.
,且每次投篮相互独立.(1)求甲得分不低于2分的概率;
(2)求乙得分的分布列及期望;
(3)甲,乙谁胜出的可能性更大?直接写出结论.
您最近半年使用:0次
解题方法
2 . 为鼓励消费,某商场开展积分奖励活动,消费满100元的顾客可拋掷骰子两次,若两次点数之和等于7,则获得5个积分:若点数之和不等于7,则获得2个积分.
(1)记两次点数之和等于7为事件A,第一次点数是奇数为事件B,证明:事件A,B是独立事件;
(2)现有3位顾客参与了这个活动,求他们获得的积分之和X的分布列和期望.
(1)记两次点数之和等于7为事件A,第一次点数是奇数为事件B,证明:事件A,B是独立事件;
(2)现有3位顾客参与了这个活动,求他们获得的积分之和X的分布列和期望.
您最近半年使用:0次
解题方法
3 . 小明从4双鞋中,随机一次取出2只,
(1)求取出的2只鞋都不来自同一双的概率;
(2)若这4双鞋中,恰有一双是小明的,记取出的2只鞋中含有小明的鞋的个数为X,求X的分布列及数学期望 ,
,
(1)求取出的2只鞋都不来自同一双的概率;
(2)若这4双鞋中,恰有一双是小明的,记取出的2只鞋中含有小明的鞋的个数为X,求X的分布列及数学期望
 ,
,
您最近半年使用:0次
2024·全国·模拟预测
4 . 2023年11月19日,以“激发创新活力,提升发展质量”为主题的第二十五届中国国际高新技术成果交易会(以下简称“高交会”)在深圳闭幕,作为“中国科技第一展”的高交会距今已有25年的历史.福田展区的专业展设有新一代信息技术展、环保展、新型显示展、智慧城市展、数字医疗展、高端装备制造展等六类.现统计了每个展区的备受关注率﹝一个展区中受到所有相关人士(或企业)关注的企业数与该展区的参展企业数的比值﹞,如下表:
(1)从参展的6个展区的企业中随机选取一家企业,求这家企业是“新型显示展”展区备受关注的企业的概率.
(2)若视备受关注率为概率,某电视台现要从“环保展”“智慧城市展”“高端装备制造展”3个展区中随机抽取2个展区,再从抽出的2个展区中各抽取一家企业进行采访,求采访的两家企业都是备受关注的企业的概率.
(3)从“新一代信息技术展”展区备受关注的企业和“数字医疗展”展区备受关注的企业中,任选2家接受记者采访.记 为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量
为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量 的分布列和数学期望.
的分布列和数学期望.
| 展区类型 | 新一代信 息技术展 | 环保展 | 新型显示展 | 智慧城市展 | 数字医疗展 | 高端装备 制造展 |
| 展区的企 业数量/家 | 60 | 360 | 650 | 450 | 70 | 990 |
| 备受关注率 | 0.20 | 0.10 | 0.24 | 0.30 | 0.10 | 0.20 |
(2)若视备受关注率为概率,某电视台现要从“环保展”“智慧城市展”“高端装备制造展”3个展区中随机抽取2个展区,再从抽出的2个展区中各抽取一家企业进行采访,求采访的两家企业都是备受关注的企业的概率.
(3)从“新一代信息技术展”展区备受关注的企业和“数字医疗展”展区备受关注的企业中,任选2家接受记者采访.记
 为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量
为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量 的分布列和数学期望.
的分布列和数学期望.
您最近半年使用:0次
解题方法
5 . 下列论述正确的有( )
A.若随机变量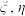 满足 满足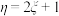 ,则 ,则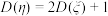 |
B.若随机事件 , , 满足: 满足: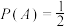 , , , , ,则事件 ,则事件 与 与 相互独立 相互独立 |
C.基于小概率值 的检验规则是:当 的检验规则是:当 时,我们就推断 时,我们就推断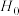 不成立,即认为 不成立,即认为 和 和 不独立,该推断犯错误的概率不超过 不独立,该推断犯错误的概率不超过 ;当 ;当 时,我们没有充分证据推断 时,我们没有充分证据推断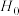 不成立,可以认为 不成立,可以认为 和 和 独立 独立 |
D.若 关于 关于 的经验回归方程为 的经验回归方程为 ,则样本点 ,则样本点 的残差为 的残差为 |
您最近半年使用:0次
6 . 某素质训练营设计了一项闯关比赛.规定:三人组队参赛,每次只派一个人,且每人只派一次:如果一个人闯关失败,再派下一个人重新闯关;三人中只要有人闯关成功即视作比赛胜利,无需继续闯关.现有甲、乙、丙三人组队参赛,他们各自闯关成功的概率分别为 、
、 、
、 ,假定
,假定 、
、 、
、 互不相等,且每人能否闯关成功的事件相互独立.
互不相等,且每人能否闯关成功的事件相互独立.
(1)计划依次派甲乙丙进行闯关,若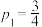 ,
,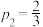 ,
,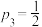 ,求该小组比赛胜利的概率;
,求该小组比赛胜利的概率;
(2)若依次派甲乙丙进行闯关,则写出所需派出的人员数目 的分布,并求
的分布,并求 的期望
的期望 ;
;
(3)已知 ,若乙只能安排在第二个派出,要使派出人员数目的期望较小,试确定甲、丙谁先派出.
,若乙只能安排在第二个派出,要使派出人员数目的期望较小,试确定甲、丙谁先派出.
 、
、 、
、 ,假定
,假定 、
、 、
、 互不相等,且每人能否闯关成功的事件相互独立.
互不相等,且每人能否闯关成功的事件相互独立.(1)计划依次派甲乙丙进行闯关,若
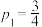 ,
,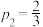 ,
,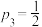 ,求该小组比赛胜利的概率;
,求该小组比赛胜利的概率;(2)若依次派甲乙丙进行闯关,则写出所需派出的人员数目
 的分布,并求
的分布,并求 的期望
的期望 ;
;(3)已知
 ,若乙只能安排在第二个派出,要使派出人员数目的期望较小,试确定甲、丙谁先派出.
,若乙只能安排在第二个派出,要使派出人员数目的期望较小,试确定甲、丙谁先派出.
您最近半年使用:0次
解题方法
7 . 随着互联网的普及、大数据的驱动,线上线下相结合的新零售时代已全面开启,新零售背景下,即时配送行业稳定快速增长.某即时配送公司为更好地了解客户需求,优化自身服务,提高客户满意度,在其 两个分公司的客户中各随机抽取10位客户进行了满意度评分调查(满分100分),评分结果如下:
两个分公司的客户中各随机抽取10位客户进行了满意度评分调查(满分100分),评分结果如下:
分公司A:66,80,72,79,80,78,87,86,91,91.
分公司B:62,77,82,70,73,86,85,94,92,89.
(1)求抽取的这20位客户评分的第一四分位数;
(2)规定评分在75分以下的为不满意,从上述不满意的客户中随机抽取3人继续沟通不满意的原因及改进建议,设被抽到的3人中分公司 的客户人数为
的客户人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
 两个分公司的客户中各随机抽取10位客户进行了满意度评分调查(满分100分),评分结果如下:
两个分公司的客户中各随机抽取10位客户进行了满意度评分调查(满分100分),评分结果如下:分公司A:66,80,72,79,80,78,87,86,91,91.
分公司B:62,77,82,70,73,86,85,94,92,89.
(1)求抽取的这20位客户评分的第一四分位数;
(2)规定评分在75分以下的为不满意,从上述不满意的客户中随机抽取3人继续沟通不满意的原因及改进建议,设被抽到的3人中分公司
 的客户人数为
的客户人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近半年使用:0次
2024·全国·模拟预测
8 . 在消费者个性化需求及文化自信等因素的影响下,汉服在中国服饰行业掀起了“国风热潮”,下表为2019—2023年中国汉服市场规模(单位:亿元),其中2019—2023年对应的年份代码依次为1~5.
(1)由上表数据可知,可用指数型函数模型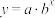 (
(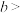 0且
0且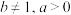 )拟合
)拟合 与
与 的关系,请建立
的关系,请建立 关于
关于 的回归方程(
的回归方程( 的值精确到0.01).
的值精确到0.01).
(2)调研数据显示,在购买汉服的消费者中,因喜欢汉服文化而购买的占 ,从购买汉服的消费者中任选5人,记这5人中因喜欢汉服文化而购买的人数与其他原因购买的人数之差为
,从购买汉服的消费者中任选5人,记这5人中因喜欢汉服文化而购买的人数与其他原因购买的人数之差为 ,求
,求 与
与 .
.
参考数据:
其中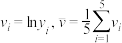 .
.
参考公式:对于一组数据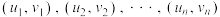 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为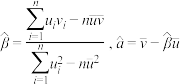 .
.
| 年份代码 | 1 | 2 | 3 | 4 | 5 |
| 市场规模 | 45 | 64 | 102 | 125 | 145 |
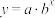 (
(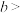 0且
0且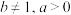 )拟合
)拟合 与
与 的关系,请建立
的关系,请建立 关于
关于 的回归方程(
的回归方程( 的值精确到0.01).
的值精确到0.01).(2)调研数据显示,在购买汉服的消费者中,因喜欢汉服文化而购买的占
 ,从购买汉服的消费者中任选5人,记这5人中因喜欢汉服文化而购买的人数与其他原因购买的人数之差为
,从购买汉服的消费者中任选5人,记这5人中因喜欢汉服文化而购买的人数与其他原因购买的人数之差为 ,求
,求 与
与 .
.参考数据:
|
|
|
|
2.31 | 35.91 | 6.90 | 1.13 |
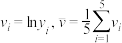 .
.参考公式:对于一组数据
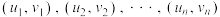 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为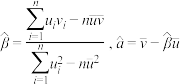 .
.
您最近半年使用:0次
2024·全国·模拟预测
9 . 某校组织了科技展参观活动,学生自愿参观,事后学校进行了一次问卷调查,分别抽取男、女生各40人作为样本.据统计:男生参观科技展的概率为 ,参观科技展的学生中女生占
,参观科技展的学生中女生占 .
.
(1)根据已知条件,填写下列 列联表,试根据小概率值
列联表,试根据小概率值 的独立性检验,分析该校学生参观科技展情况与性别是否有关.
的独立性检验,分析该校学生参观科技展情况与性别是否有关.
(2)用分层随机抽样的方式从参观科技展的人中抽取12人,再从这12人中随机抽取6人,用随机变量 表示女生人数,求
表示女生人数,求 的分布列和数学期望.
的分布列和数学期望.
参考公式和数据: ,其中
,其中 .
.
 ,参观科技展的学生中女生占
,参观科技展的学生中女生占 .
.(1)根据已知条件,填写下列
 列联表,试根据小概率值
列联表,试根据小概率值 的独立性检验,分析该校学生参观科技展情况与性别是否有关.
的独立性检验,分析该校学生参观科技展情况与性别是否有关.| 参观科技展 | 未参观科技展 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
 表示女生人数,求
表示女生人数,求 的分布列和数学期望.
的分布列和数学期望.参考公式和数据:
 ,其中
,其中 .
. | 0.1 | 0.05 | 0.025 | 0.01 | 0.001 |
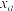 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
您最近半年使用:0次
解题方法
10 . 盒中有标记数字1,2的小球各2个.
(1)若有放回地随机取出2个小球,求取出的2个小球上的数字不同的概率;
(2)若不放回地依次随机取出4个小球,记相邻小球上的数字相同的对数为 (如1122,则
(如1122,则 ),求
),求 的分布列及数学期望
的分布列及数学期望 .
.
(1)若有放回地随机取出2个小球,求取出的2个小球上的数字不同的概率;
(2)若不放回地依次随机取出4个小球,记相邻小球上的数字相同的对数为
 (如1122,则
(如1122,则 ),求
),求 的分布列及数学期望
的分布列及数学期望 .
.
您最近半年使用:0次