2024·全国·模拟预测
1 . 2023年11月10日,第六届中国国际进口博览会圆满落下帷幕.在各方共同努力和大力支持下,本届进博会办成了一届高标准、高质量、高水平的全球经贸盛会,为世界经济复苏和全球发展繁荣做出积极贡献.本届进博会优化了志愿者服务,为参展商提供了更加准确、细致的服务.为了解参展商对志愿者服务的满意度,组委会组织了所有的参展商对志愿者服务进行评分(满分100分),并从评分结果中随机抽取100份进行统计,按照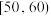 ,
,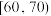 ,
,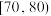 ,
,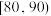 ,
, 进行分组,得到如图所示的频率分布直方图.
进行分组,得到如图所示的频率分布直方图.

(1)求出 的值和参展商对志愿者服务评分的平均数(同一组中的数据用该组区间的中点值为代表).
的值和参展商对志愿者服务评分的平均数(同一组中的数据用该组区间的中点值为代表).
(2)以频率估计概率,样本估计总体,从所有参展商的评分结果中随机抽取3份,将 记为评分不低于90分的份数,求
记为评分不低于90分的份数,求 的分布列和数学期望.
的分布列和数学期望.
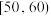 ,
,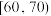 ,
,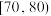 ,
,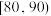 ,
, 进行分组,得到如图所示的频率分布直方图.
进行分组,得到如图所示的频率分布直方图.
(1)求出
 的值和参展商对志愿者服务评分的平均数(同一组中的数据用该组区间的中点值为代表).
的值和参展商对志愿者服务评分的平均数(同一组中的数据用该组区间的中点值为代表).(2)以频率估计概率,样本估计总体,从所有参展商的评分结果中随机抽取3份,将
 记为评分不低于90分的份数,求
记为评分不低于90分的份数,求 的分布列和数学期望.
的分布列和数学期望.
您最近半年使用:0次
2 . 下列说法中正确的是( )
A.已知随机事件A,B满足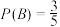 , ,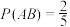 ,则 ,则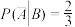 |
B.已知随机变量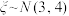 ,若 ,若 ,则 ,则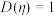 |
C.若样本数据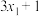 , ,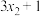 ,…, ,…, 的平均数为10,则数据 的平均数为10,则数据 的平均数为3 的平均数为3 |
D.随机变量X服从二项分布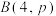 ,若方差 ,若方差 ,则 ,则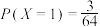 |
您最近半年使用:0次
名校
解题方法
3 . 现从含甲、乙在内的10名特种兵中选出4人去参加抢险,则在甲被选中的前提下,乙也被选中的概率为( )
A. | B. | C. | D. |
您最近半年使用:0次
今日更新
|
1991次组卷
|
4卷引用:青海湟川中学2023-2024学年高三下学期第一次模拟考试数学(理)试卷
青海湟川中学2023-2024学年高三下学期第一次模拟考试数学(理)试卷(已下线)第五套 艺体生新高考全真模拟 (一模重组卷)河北省衡水市武强中学2023-2024学年高二下学期期中考试数学试题(已下线)模块3 第7套 复盘卷(高三重组卷)
名校
解题方法
4 . 箱子中装有 个大小相同的小球,其中
个大小相同的小球,其中 个红球、
个红球、 个白球.从中随机抽出
个白球.从中随机抽出 个球,在已知抽到红球的条件下,
个球,在已知抽到红球的条件下, 个球都是红球的概率为
个球都是红球的概率为___________ .
 个大小相同的小球,其中
个大小相同的小球,其中 个红球、
个红球、 个白球.从中随机抽出
个白球.从中随机抽出 个球,在已知抽到红球的条件下,
个球,在已知抽到红球的条件下, 个球都是红球的概率为
个球都是红球的概率为
您最近半年使用:0次
解题方法
5 . 某单位选派一支代表队参加市里的辩论比赛,现有“初心”“使命”两支预备队.选哪支队是随机的,其中选“初心”队获胜的概率为0.8,选“使命”队获胜的概率为0.7,单位在比赛中获胜的条件下,选“使命”队参加比赛的概率为( )
A.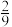 | B. | C. | D.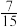 |
您最近半年使用:0次
2024·全国·模拟预测
6 . 2023年11月19日,以“激发创新活力,提升发展质量”为主题的第二十五届中国国际高新技术成果交易会(以下简称“高交会”)在深圳闭幕,作为“中国科技第一展”的高交会距今已有25年的历史.福田展区的专业展设有新一代信息技术展、环保展、新型显示展、智慧城市展、数字医疗展、高端装备制造展等六类.现统计了每个展区的备受关注率﹝一个展区中受到所有相关人士(或企业)关注的企业数与该展区的参展企业数的比值﹞,如下表:
(1)从参展的6个展区的企业中随机选取一家企业,求这家企业是“新型显示展”展区备受关注的企业的概率.
(2)若视备受关注率为概率,某电视台现要从“环保展”“智慧城市展”“高端装备制造展”3个展区中随机抽取2个展区,再从抽出的2个展区中各抽取一家企业进行采访,求采访的两家企业都是备受关注的企业的概率.
(3)从“新一代信息技术展”展区备受关注的企业和“数字医疗展”展区备受关注的企业中,任选2家接受记者采访.记 为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量
为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量 的分布列和数学期望.
的分布列和数学期望.
| 展区类型 | 新一代信 息技术展 | 环保展 | 新型显示展 | 智慧城市展 | 数字医疗展 | 高端装备 制造展 |
| 展区的企 业数量/家 | 60 | 360 | 650 | 450 | 70 | 990 |
| 备受关注率 | 0.20 | 0.10 | 0.24 | 0.30 | 0.10 | 0.20 |
(2)若视备受关注率为概率,某电视台现要从“环保展”“智慧城市展”“高端装备制造展”3个展区中随机抽取2个展区,再从抽出的2个展区中各抽取一家企业进行采访,求采访的两家企业都是备受关注的企业的概率.
(3)从“新一代信息技术展”展区备受关注的企业和“数字医疗展”展区备受关注的企业中,任选2家接受记者采访.记
 为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量
为这2家企业中来自“新一代信息技术展”展区的企业数量,求随机变量 的分布列和数学期望.
的分布列和数学期望.
您最近半年使用:0次
解题方法
7 . ChatGPT是OpenAI研发的一款聊天机器人程序,是人工智能技术驱动的自然语言处理工具,它能够基于在预训练阶段所见的模式和统计规律来生成回答,但它的回答可能会受到训练数据信息的影响,不一定完全正确.某科技公司在使用ChatGPT对某一类问题进行测试时发现,如果输入的问题没有语法错误,它回答正确的概率为0.98;如果出现语法错误,它回答正确的概率为0.18. 假设每次输入的问题出现语法错误的概率为0.1,且每次输入问题,ChatGPT的回答是否正确相互独立.该公司科技人员小张想挑战一下ChatGPT,小张和ChatGPT各自从给定的10个问题中随机抽取9个作答,已知在这10个问题中,小张能正确作答其中的9个.
(1)求小张能全部回答正确的概率;
(2)求一个问题能被ChatGPT回答正确的概率;
(3)在这轮挑战中,分别求出小张和ChatGPT答对题数的期望与方差.
(1)求小张能全部回答正确的概率;
(2)求一个问题能被ChatGPT回答正确的概率;
(3)在这轮挑战中,分别求出小张和ChatGPT答对题数的期望与方差.
您最近半年使用:0次
8 . 已知甲社区有120人计划去四川旅游,他们每人将从峨眉山与青城山中选择一个去旅游,将这120人分为东、西两小组,两组的人数相等,已知东小组中去峨眉山的人数是去青城山人数的两倍,西小组中去峨眉山的人数比去青城山的人数少10.
(1)完成下面的 列联表,并判断是否有99%的把握认为游客的选择与所在的小组有关;
列联表,并判断是否有99%的把握认为游客的选择与所在的小组有关;
(2)在东小组的游客中,以他们去青城山旅游的频率为乙社区游客去青城山旅游的概率,从乙社区任选3名游客,记这3名游客中去青城山旅游的人数为X,求 及X的数学期望.
及X的数学期望.
参考公式: ,
, .
.
(1)完成下面的
 列联表,并判断是否有99%的把握认为游客的选择与所在的小组有关;
列联表,并判断是否有99%的把握认为游客的选择与所在的小组有关;去峨眉山旅游 | 去青城山旅游 | 合计 | |
东小组 | |||
西小组 | |||
合计 |
 及X的数学期望.
及X的数学期望.参考公式:
 ,
, .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
解题方法
9 . 某区高三年级3200名学生参加了区统一考试.已知考试成绩 服从正态分布
服从正态分布 (试卷满分为150分).统计结果显示,考试成绩在80分到120分之间的人数约为总人数的
(试卷满分为150分).统计结果显示,考试成绩在80分到120分之间的人数约为总人数的 ,则此次考试中成绩不低于120分的学生人数约为( )
,则此次考试中成绩不低于120分的学生人数约为( )
 服从正态分布
服从正态分布 (试卷满分为150分).统计结果显示,考试成绩在80分到120分之间的人数约为总人数的
(试卷满分为150分).统计结果显示,考试成绩在80分到120分之间的人数约为总人数的 ,则此次考试中成绩不低于120分的学生人数约为( )
,则此次考试中成绩不低于120分的学生人数约为( )| A.350 | B.400 | C.450 | D.500 |
您最近半年使用:0次
名校
解题方法
10 . 元旦前夕天津-中图书馆举办一年一度“猜灯谜”活动,灯谜题目中逻辑推理占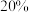 ,传统灯谜占
,传统灯谜占 ,一中文化占
,一中文化占 ,小伟同学答对逻辑推理,传统灯谜,一中文化的概率分别为
,小伟同学答对逻辑推理,传统灯谜,一中文化的概率分别为 ,
,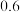 ,
,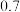 ,若小伟同学任意抽取一道题目作答,则答对题目的概率为
,若小伟同学任意抽取一道题目作答,则答对题目的概率为______ ,若小伟同学运用“超能力”,抽到的5道题都是逻辑推理题,则这5道题目中答对题目个数 的数学期望为
的数学期望为______ .
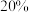 ,传统灯谜占
,传统灯谜占 ,一中文化占
,一中文化占 ,小伟同学答对逻辑推理,传统灯谜,一中文化的概率分别为
,小伟同学答对逻辑推理,传统灯谜,一中文化的概率分别为 ,
,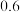 ,
,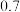 ,若小伟同学任意抽取一道题目作答,则答对题目的概率为
,若小伟同学任意抽取一道题目作答,则答对题目的概率为 的数学期望为
的数学期望为
您最近半年使用:0次





