1 . 会员足够多的某知名咖啡店,男会员占60%,女会员占40%.现对会员进行服务质量满意度调查.根据调查结果得知,男会员对服务质量满意的概率为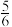 ,女会员对服务质量满意的概率为
,女会员对服务质量满意的概率为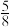 .
.
(1)随机选取一名会员,求其对服务质量满意的概率;
(2)从会员中随机抽取3人,记抽取的3人中,对服务质量满意的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
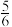 ,女会员对服务质量满意的概率为
,女会员对服务质量满意的概率为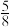 .
.(1)随机选取一名会员,求其对服务质量满意的概率;
(2)从会员中随机抽取3人,记抽取的3人中,对服务质量满意的人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近半年使用:0次
2 . 小明参加社区组织的射击比赛活动,已知小明射击一次、击中区域甲的概率是 ,击中区域乙的概率是
,击中区域乙的概率是 ,击中区域丙的概率是
,击中区域丙的概率是 ,区域甲,乙、丙均没有重复的部分.这次射击比赛获奖规则是:若击中区域甲则获一等奖;若击中区域乙则有一半的机会获得二等奖,有一半的机会获得三等奖;若击中区域丙则获得三等奖;若击中上述三个区域以外的区域则不获奖.获得一等奖和二等奖的选手被评为“优秀射击手”称号.
,区域甲,乙、丙均没有重复的部分.这次射击比赛获奖规则是:若击中区域甲则获一等奖;若击中区域乙则有一半的机会获得二等奖,有一半的机会获得三等奖;若击中区域丙则获得三等奖;若击中上述三个区域以外的区域则不获奖.获得一等奖和二等奖的选手被评为“优秀射击手”称号.
(1)求小明射击1次获得“优秀射击手”称号的概率;
(2)小明在比赛中射击4次,每次射击的结果相互独立,设获三等奖的次数为X,求X分布列和数学期望.
 ,击中区域乙的概率是
,击中区域乙的概率是 ,击中区域丙的概率是
,击中区域丙的概率是 ,区域甲,乙、丙均没有重复的部分.这次射击比赛获奖规则是:若击中区域甲则获一等奖;若击中区域乙则有一半的机会获得二等奖,有一半的机会获得三等奖;若击中区域丙则获得三等奖;若击中上述三个区域以外的区域则不获奖.获得一等奖和二等奖的选手被评为“优秀射击手”称号.
,区域甲,乙、丙均没有重复的部分.这次射击比赛获奖规则是:若击中区域甲则获一等奖;若击中区域乙则有一半的机会获得二等奖,有一半的机会获得三等奖;若击中区域丙则获得三等奖;若击中上述三个区域以外的区域则不获奖.获得一等奖和二等奖的选手被评为“优秀射击手”称号.(1)求小明射击1次获得“优秀射击手”称号的概率;
(2)小明在比赛中射击4次,每次射击的结果相互独立,设获三等奖的次数为X,求X分布列和数学期望.
您最近半年使用:0次
昨日更新
|
1425次组卷
|
3卷引用:广东省韶关市2024届高三综合测试(二)数学试题
3 . 2024年3月,某校语文教师对学生提出“3月读一本书”的要求,每位学生都选择且只能选择《红楼梦》和《三国演义》中的一本,现随机调查该校男、女生各100人,发现选择《红楼梦》的有90人,其中女生占 .
.
(1)补充完整下述 列联表,并判断能否有
列联表,并判断能否有 的把握认为学生选择《红楼梦》还是《三国演义》与性别有关;
的把握认为学生选择《红楼梦》还是《三国演义》与性别有关;
(2)已知学生选择哪本书是相互独立的,用频率代替概率,从该校选择《红楼梦》的学生中随机抽取3人,抽到的女生人数设为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式: ,其中
,其中 .
.
参考数据:
 .
.(1)补充完整下述
 列联表,并判断能否有
列联表,并判断能否有 的把握认为学生选择《红楼梦》还是《三国演义》与性别有关;
的把握认为学生选择《红楼梦》还是《三国演义》与性别有关;| 《红楼梦》 | 《三国演义》 | |
| 男生 | ||
| 女生 |
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.参考公式:
 ,其中
,其中 .
.参考数据:
 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
4 . 某药厂生产的一种药品,声称对某疾病的有效率为80%.若该药对患有该疾病的病人有效,病人服用该药一个疗程,有90%的可能性治愈,有10%的可能性没有治愈;若该药对患有该疾病的病人无效,病人服用该药一个疗程,有40%的可能性自愈,有60%的可能性没有自愈.
(1)若该药厂声称的有效率是真实的,利用该药治疗3个患有该疾病的病人,记一个疗程内康复的人数为 ,求随机变量
,求随机变量 的分布列和期望;
的分布列和期望;
(2)一般地,当 比较大时,离散型的二项分布可以近似地看成连续型的正态分布,若
比较大时,离散型的二项分布可以近似地看成连续型的正态分布,若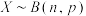 ,则
,则 可以近似看成随机变量
可以近似看成随机变量 ,
, ,其中
,其中 ,
, ,对整数
,对整数 ,
, (
( ),
),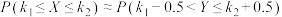 .现为了检验此药的有效率,任意抽取100个此种病患者进行药物临床试验,如果一个疗程内至少有
.现为了检验此药的有效率,任意抽取100个此种病患者进行药物临床试验,如果一个疗程内至少有 人康复,则此药通过检验.现要求:若此药的实际有效率为
人康复,则此药通过检验.现要求:若此药的实际有效率为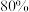 ,通过检验的概率不低于0.9772,求整数
,通过检验的概率不低于0.9772,求整数 的最大值.(参考数据:若
的最大值.(参考数据:若 ,则
,则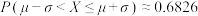 ,
,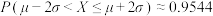 ,
,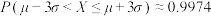 )
)
(1)若该药厂声称的有效率是真实的,利用该药治疗3个患有该疾病的病人,记一个疗程内康复的人数为
 ,求随机变量
,求随机变量 的分布列和期望;
的分布列和期望;(2)一般地,当
 比较大时,离散型的二项分布可以近似地看成连续型的正态分布,若
比较大时,离散型的二项分布可以近似地看成连续型的正态分布,若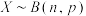 ,则
,则 可以近似看成随机变量
可以近似看成随机变量 ,
, ,其中
,其中 ,
, ,对整数
,对整数 ,
, (
( ),
),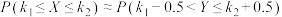 .现为了检验此药的有效率,任意抽取100个此种病患者进行药物临床试验,如果一个疗程内至少有
.现为了检验此药的有效率,任意抽取100个此种病患者进行药物临床试验,如果一个疗程内至少有 人康复,则此药通过检验.现要求:若此药的实际有效率为
人康复,则此药通过检验.现要求:若此药的实际有效率为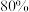 ,通过检验的概率不低于0.9772,求整数
,通过检验的概率不低于0.9772,求整数 的最大值.(参考数据:若
的最大值.(参考数据:若 ,则
,则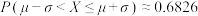 ,
,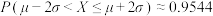 ,
,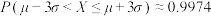 )
)
您最近半年使用:0次
5 . 流感病毒是一种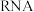 病毒,大致分为甲型、乙型、丙型三种,其中甲流病毒传染性最强,致死率最高,危害也最大.某药品科技研发团队针对甲流病毒的特点,研发出预防甲流药品
病毒,大致分为甲型、乙型、丙型三种,其中甲流病毒传染性最强,致死率最高,危害也最大.某药品科技研发团队针对甲流病毒的特点,研发出预防甲流药品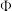 和治疗甲流药品
和治疗甲流药品 ,根据研发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2列联表:
,根据研发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2列联表:
(1)根据 的独立性检验,分析预防药品
的独立性检验,分析预防药品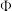 对预防甲流的有效性;
对预防甲流的有效性;
(2)用频率估计概率,从已经感染的动物中,采用随机抽样方式每次选出1只,用治疗药品 对该动物进行治疗,已知治疗药品
对该动物进行治疗,已知治疗药品 的治愈数据如下:对未使用过预防药品
的治愈数据如下:对未使用过预防药品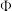 的动物的治愈率为0.5,对使用过预防药品
的动物的治愈率为0.5,对使用过预防药品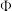 的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染动物中被治愈的动物只数为
的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染动物中被治愈的动物只数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
附: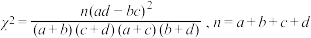 .
.
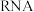 病毒,大致分为甲型、乙型、丙型三种,其中甲流病毒传染性最强,致死率最高,危害也最大.某药品科技研发团队针对甲流病毒的特点,研发出预防甲流药品
病毒,大致分为甲型、乙型、丙型三种,其中甲流病毒传染性最强,致死率最高,危害也最大.某药品科技研发团队针对甲流病毒的特点,研发出预防甲流药品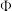 和治疗甲流药品
和治疗甲流药品 ,根据研发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2列联表:
,根据研发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2列联表:预防药品 | 甲流病毒 | 合计 | |
感染 | 未感染 | ||
未使用 | 24 | 21 | 45 |
使用 | 16 | 39 | 55 |
合计 | 40 | 60 | 100 |
 的独立性检验,分析预防药品
的独立性检验,分析预防药品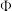 对预防甲流的有效性;
对预防甲流的有效性;(2)用频率估计概率,从已经感染的动物中,采用随机抽样方式每次选出1只,用治疗药品
 对该动物进行治疗,已知治疗药品
对该动物进行治疗,已知治疗药品 的治愈数据如下:对未使用过预防药品
的治愈数据如下:对未使用过预防药品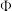 的动物的治愈率为0.5,对使用过预防药品
的动物的治愈率为0.5,对使用过预防药品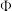 的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染动物中被治愈的动物只数为
的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染动物中被治愈的动物只数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.附:
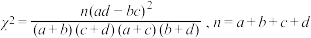 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
解题方法
6 . 某中学为了解本校高二年级学生阅读水平现状,从该年级学生中随机抽取100人进行一般现代文阅读速度的测试,以每位学生平均每分钟阅读的字数作为该学生的阅读速度,将测试结果整理得到如下频率分布直方图:
(2)用频率估计概率,从该校高二学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为 ,求
,求 的分布列与数学期望
的分布列与数学期望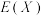 ;
;
(3)若某班有10名学生参加测试,他们的阅读速度如下:506,516,553,592,617,632,667,693,723,776,从这10名学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为 ,试判断数学期望
,试判断数学期望 与(2)中的
与(2)中的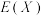 的大小.(结论不要求证明)
的大小.(结论不要求证明)
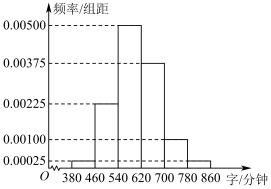
(2)用频率估计概率,从该校高二学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为
 ,求
,求 的分布列与数学期望
的分布列与数学期望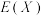 ;
;(3)若某班有10名学生参加测试,他们的阅读速度如下:506,516,553,592,617,632,667,693,723,776,从这10名学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为
 ,试判断数学期望
,试判断数学期望 与(2)中的
与(2)中的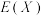 的大小.(结论不要求证明)
的大小.(结论不要求证明)
您最近半年使用:0次
名校
解题方法
7 . 如图所示,已知一质点在外力的作用下,从原点 出发,每次向左移动的概率为
出发,每次向左移动的概率为 ,向右移动的概率为
,向右移动的概率为 .若该质点每次移动一个单位长度,设经过5次移动后,该质点位于
.若该质点每次移动一个单位长度,设经过5次移动后,该质点位于 的位置,则
的位置,则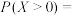 ( )
( )
 出发,每次向左移动的概率为
出发,每次向左移动的概率为 ,向右移动的概率为
,向右移动的概率为 .若该质点每次移动一个单位长度,设经过5次移动后,该质点位于
.若该质点每次移动一个单位长度,设经过5次移动后,该质点位于 的位置,则
的位置,则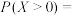 ( )
( )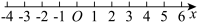
A. | B.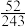 | C.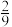 | D. |
您最近半年使用:0次
7日内更新
|
1647次组卷
|
4卷引用:华大新高考联盟2024届高三4月教学质量测评理科数学试题(老教材全国卷)
解题方法
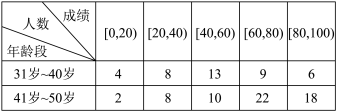
8 . 中医药学是中国古代科学的瑰宝,也是打开中华文明宝库的钥匙.为了调查某地市民对中医药文化的了解程度,某学习小组随机向该地100位不同年龄段的市民发放了有关中医药文化的调查问卷,得到的数据如下表所示: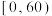 内代表对中医药文化了解程度低,成绩在
内代表对中医药文化了解程度低,成绩在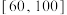 内代表对中医药文化了解程度高.
内代表对中医药文化了解程度高.
(1)从这100位市民中随机抽取1人,求抽到对中医药文化了解程度高的市民的频率;
(2)将频率视为概率,现从该地41岁~50岁年龄段的市民中随机抽取3人,记 为对中医药文化了解程度高的人数,求
为对中医药文化了解程度高的人数,求 的分布列和期望.
的分布列和期望.
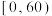 内代表对中医药文化了解程度低,成绩在
内代表对中医药文化了解程度低,成绩在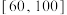 内代表对中医药文化了解程度高.
内代表对中医药文化了解程度高. (1)从这100位市民中随机抽取1人,求抽到对中医药文化了解程度高的市民的频率;
(2)将频率视为概率,现从该地41岁~50岁年龄段的市民中随机抽取3人,记
 为对中医药文化了解程度高的人数,求
为对中医药文化了解程度高的人数,求 的分布列和期望.
的分布列和期望.
您最近半年使用:0次
7日内更新
|
307次组卷
|
7卷引用:河南省南阳地区2023-2024学年高二上学期期末热身摸底联考数学试题
河南省南阳地区2023-2024学年高二上学期期末热身摸底联考数学试题陕西省西安市鄠邑区2023-2024学年高三上学期期末考试(理科)数学试题2024届高三新高考改革数学适应性练习(九省联考题型)(已下线)7.4.1 二项分布(分层练习,6大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)8.2 离散型随机变量及其分布列(3)(已下线)8.2 离散型随机变量及其分布列(1)(已下线)第七章 随机变量及其分布总结 第一课 解透课本内容
2024·全国·模拟预测
9 . 某市物理教研员在一次高二全市统考后为了了解本市物理考试情况,从全市高二参加考试的学生中随机抽取50名学生对其物理成绩(单位:分,成绩都在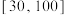 内)进行统计,制成频率分布直方图如图所示:
内)进行统计,制成频率分布直方图如图所示: 的值,并以样本估计总体,求本次高二全市统考物理成绩的中位数(同一组中的数据用该组区间的中点值为代表);
的值,并以样本估计总体,求本次高二全市统考物理成绩的中位数(同一组中的数据用该组区间的中点值为代表);
(2)从该市高二参加考试的学生中随机抽取3人,记这3人中物理考试成绩在 内的人数为
内的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
 内)进行统计,制成频率分布直方图如图所示:
内)进行统计,制成频率分布直方图如图所示: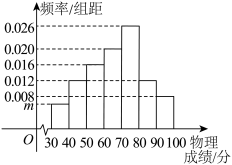
 的值,并以样本估计总体,求本次高二全市统考物理成绩的中位数(同一组中的数据用该组区间的中点值为代表);
的值,并以样本估计总体,求本次高二全市统考物理成绩的中位数(同一组中的数据用该组区间的中点值为代表);(2)从该市高二参加考试的学生中随机抽取3人,记这3人中物理考试成绩在
 内的人数为
内的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
您最近半年使用:0次
解题方法
10 . 一质子从原点处出发,每次等可能地向左、向右、向上或向下移动一个单位长度,则移动6次后质子回到原点处的概率是( )
A. | B.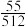 | C.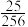 | D.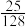 |
您最近半年使用:0次





