名校
解题方法
1 . 近日海南文旅火爆出圈,海南岛优美的海滨景观和深厚的文化底蕴吸引着全国各地游客前往,小明计划假期去海口、三亚、儋州、文昌、琼海五个城市游玩,每个城市都去且只去一次,若儋州和文昌这两个城市不排在最前面和最后面,则不同的游玩顺序有______ 种.(用数字作答)
您最近半年使用:0次
名校
解题方法
2 . 黄山是中国著名的旅游胜地,有许多值得打卡的旅游景点,其中包括黄山风景区,齐云山,宏村,徽州古城等. 甲,乙,丙
甲,乙,丙 人准备前往黄山风景区,齐云山,宏村,徽州古城这
人准备前往黄山风景区,齐云山,宏村,徽州古城这 个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩.若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )
个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩.若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )
 甲,乙,丙
甲,乙,丙 人准备前往黄山风景区,齐云山,宏村,徽州古城这
人准备前往黄山风景区,齐云山,宏村,徽州古城这 个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩.若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )
个景点游玩,其中甲和乙已经去过黄山风景区,本次不再前往黄山风景区游玩.若甲,乙,丙每人选择一个或两个景点游玩,则不同的选择有( )A. 种 种 | B.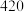 种 种 | C. 种 种 | D. 种 种 |
您最近半年使用:0次
3 . 2024年3月16日下午3点,在贵州省黔东南苗族侗族自治州榕江县“村超”足球场,伴随平地村足球队在对阵口寨村足球队中踢出的第一脚球,2024年第二届贵州“村超”总决赛阶段的比赛正式拉开帷幕.某校足球社的五位同学准备前往村超球队所在村寨调研,将在第一天前往平地村、口寨村、忠诚村,已知每个村至少有一位同学前往,五位同学都会进行选择并且每位同学只能选择其中一个村,若学生甲和学生乙必须选同一个村,则不同的选法种数是( )
| A.18 | B.36 | C.54 | D.72 |
您最近半年使用:0次
解题方法
4 . 有0,1,2,3,4五个数字,问:
(1)可以组成多少个无重复数字的四位密码?
(2)可以组成多少个无重复数字的四位数?
(1)可以组成多少个无重复数字的四位密码?
(2)可以组成多少个无重复数字的四位数?
您最近半年使用:0次
5 . 下列说法正确的有( )
| A.某小组有8名男生,4名女生,要从中选取一名当组长,不同的选法有12种 |
| B.某小组有3名男生,4名女生,要从中选取两名同学,不同的选法有42种 |
| C.两位同学同时去乘坐地铁,一列地铁有6节车厢,两人乘坐车厢的方法共有36种 |
| D.甲、乙、丙、丁、戊五人并排站成一排,甲乙不相邻的排法有82种 |
您最近半年使用:0次
昨日更新
|
280次组卷
|
2卷引用:宁夏回族自治区石嘴山市第一中学2023-2024学年高二下学期3月月考数学试题
6 . 房屋建造时经常需要把长方体砖头进行不同角度的切割,以契合实际需要.已知长方体的规格为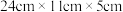 ,现从长方体的某一棱的中点处作垂直于该棱的截面,截取1次后共可以得到
,现从长方体的某一棱的中点处作垂直于该棱的截面,截取1次后共可以得到 ,
,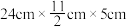 ,
, 三种不同规格的长方体.按照上述方式对第1次所截得的长方体进行第2次截取,再对第2次所截得的长方体进行第3次截取,则共可得到体积为165cm³的不同规格长方体的个数为( )
三种不同规格的长方体.按照上述方式对第1次所截得的长方体进行第2次截取,再对第2次所截得的长方体进行第3次截取,则共可得到体积为165cm³的不同规格长方体的个数为( )
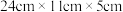 ,现从长方体的某一棱的中点处作垂直于该棱的截面,截取1次后共可以得到
,现从长方体的某一棱的中点处作垂直于该棱的截面,截取1次后共可以得到 ,
,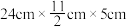 ,
, 三种不同规格的长方体.按照上述方式对第1次所截得的长方体进行第2次截取,再对第2次所截得的长方体进行第3次截取,则共可得到体积为165cm³的不同规格长方体的个数为( )
三种不同规格的长方体.按照上述方式对第1次所截得的长方体进行第2次截取,再对第2次所截得的长方体进行第3次截取,则共可得到体积为165cm³的不同规格长方体的个数为( )
| A.8 | B.10 | C.12 | D.16 |
您最近半年使用:0次
解题方法
7 . 已知某校开设4门选修课供同学们选择,现有甲、乙、丙三名同学进行选课,每人必须选择一门课程,则这3名同学不同的选课情况共有________ 种.
您最近半年使用:0次
8 . 从0,1,2,3,4中选出3个数组成各位数字不重复的三位偶数,这样的数有( )个.
| A.24 | B.30 | C.36 | D.60 |
您最近半年使用:0次
昨日更新
|
1508次组卷
|
5卷引用:重庆市巴蜀中学校2023-2024学年高二下学期第一次月考数学试卷
重庆市巴蜀中学校2023-2024学年高二下学期第一次月考数学试卷(已下线)6.1 分类加法计数原理与分步乘法计数原理(6大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)6.2.1&6.2.2 排列、排列数(6大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)北京市第九中学2023-2024学年高二下学期4月月考数学试卷山东省淄博市实验中学2023-2024学年高二下学期第一次月考(3月)数学试卷
解题方法
9 . 某校组队参加辩论赛,从6名学生中选出4人分别担任一、三、三、四辩,若其中学生甲必须参定且不担任四辩,则不同的安排方法种数为( )
| A.180 | B.120 | C.90 | D.240 |
您最近半年使用:0次
解题方法
10 . 已知全集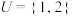 ,集合
,集合 为
为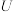 的子集,则有序集合
的子集,则有序集合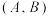 一共有
一共有______ 组.
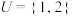 ,集合
,集合 为
为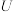 的子集,则有序集合
的子集,则有序集合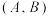 一共有
一共有
您最近半年使用:0次



