解题方法
1 . 用0，1，2，3，4，5这6个数字，求：
(1)组成没有重复数字的四位偶数的个数；
(2)组成无重复数字且大于4000的自然数的个数．
(1)组成没有重复数字的四位偶数的个数；
(2)组成无重复数字且大于4000的自然数的个数．
您最近半年使用：0次
2 . 将
六位教师分配到3所学校，若每所学校分配2人，其中
分配到同一所学校，则不同的分配方法共有（ ）
六位教师分配到3所学校，若每所学校分配2人，其中分配到同一所学校，则不同的分配方法共有（ ）| A．12种 | B．18种 | C．36种 | D．54种 |
您最近半年使用：0次
解题方法
3 . 为助力乡村振兴，九江市教科所计划选派5名党员教师前往5个乡村开展“五育”支教进乡村党建活动，每个乡村有且只有1人，则甲不派往乡村A的选派方法有________ 种.
您最近半年使用：0次
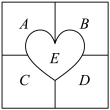
4 . 如图，某心形花坛中有A，B，C，D，E5个区域，每个区域只种植一种颜色的花．
(2)要把4种不同颜色的花种植到这5个区域中，每种颜色的花都必须种植，共有多少种不同的种植方案？
(3)要把红、黄、蓝、白4种不同颜色的花种植到这5个区域中，每种颜色的花都必须种植，要求相同颜色的花不能相邻种植，且有两个相邻的区域种植红、黄2种不同颜色的花，共有多少种不同的种植方案？
(2)要把4种不同颜色的花种植到这5个区域中，每种颜色的花都必须种植，共有多少种不同的种植方案？
(3)要把红、黄、蓝、白4种不同颜色的花种植到这5个区域中，每种颜色的花都必须种植，要求相同颜色的花不能相邻种植，且有两个相邻的区域种植红、黄2种不同颜色的花，共有多少种不同的种植方案？
您最近半年使用：0次
5 . 五人（含甲、乙）排成一排照相，排法正确的是（ ）
| A．甲、乙必须站在一起，共有48种站法 |
| B．甲、乙不站在一起，共有36种站法 |
| C．甲、乙必须站两端，共有12种站法 |
| D．甲不站排头，乙不站排尾，共有78种站法 |
您最近半年使用：0次
6 . 4名男生和3名女生站成一排．
(1)甲、乙两人必须站在两端的站法有多少种？
(2)甲、乙相邻且与丙不相邻的站法有几种？
(3)甲、乙、丙三人从左到右顺序一定的站法有多少种？
(1)甲、乙两人必须站在两端的站法有多少种？
(2)甲、乙相邻且与丙不相邻的站法有几种？
(3)甲、乙、丙三人从左到右顺序一定的站法有多少种？
您最近半年使用：0次
名校
解题方法
7 . 用0，1，2，3，4组成无重复数字的三位偶数有（ ）
| A．24个 | B．30个 | C．40个 | D．48个 |
您最近半年使用：0次
2024高二下·全国·专题练习
解题方法
8 . 有10名演员，其中8人会唱歌，5人会跳舞，现要表演一个2人唱歌2人伴舞的节目，则不同的选派方法共有______ 种.
您最近半年使用：0次
9 . 某市举行乡村振兴汇报会，六个获奖单位的负责人甲､乙､丙等六人分别上台发言，其中负责人甲､乙发言顺序必须相邻，丙不能在第一个与最后一个发言，则不同的安排方法共有（ ）
| A．240种 | B．120种 | C．156种 | D．144种 |
您最近半年使用：0次
10 . 在实验中学元旦晚会中有A、B、C、D、E，5个节目，为了考虑整体效果，对节目演出顺序有如下具体要求，节目A不能安排在第一位和最后一位，节目D、E必须安排连在一起，则这五个节目演出顺序的编排方案共有______ 种．
您最近半年使用：0次
