名校
解题方法
1 . 将甲、乙、丙、丁四人安排到篮球与演讲比赛现场进行任务工作,每个比赛现场需要两人,则甲、乙安排在一起的概率为______ .
您最近半年使用:0次
解题方法
2 . 第19届亚运会的样物由“琮琮”“宸宸”和“莲莲”三类组成,现有印着三类吉祥物的挂件各2个 同类吉祥物完全相同,无区别
同类吉祥物完全相同,无区别 ,若把这6个挂件分给3位同学,每人2个,则恰好有一位同学得到同类吉祥物挂件的概率是( )
,若把这6个挂件分给3位同学,每人2个,则恰好有一位同学得到同类吉祥物挂件的概率是( )
 同类吉祥物完全相同,无区别
同类吉祥物完全相同,无区别 ,若把这6个挂件分给3位同学,每人2个,则恰好有一位同学得到同类吉祥物挂件的概率是( )
,若把这6个挂件分给3位同学,每人2个,则恰好有一位同学得到同类吉祥物挂件的概率是( )A.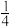 | B.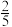 | C.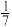 | D. |
您最近半年使用:0次
名校
解题方法
3 . 某款对战游戏,总有一定比例的玩家作弊该游戏每10个人组成一组对局,若一组对局中有作弊玩家,则认为这组对局不公平.现有50名玩家,其中有2名玩家为作弊玩家,一次性将50名玩家平均分为5组,则5组对局中,恰有一组对局为不公平对局的概率为( )
A.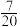 | B. | C.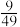 | D. |
您最近半年使用:0次
2023-11-07更新
|
814次组卷
|
2卷引用:云南师范大学附属中学2024届高三上学期高考适应性月考卷(四)数学试题
解题方法
4 . 春节前夕,某街道办事处为某小区老年人送慰问品,需招募10名志愿者,分成两组,每组5人,共有15人报了名.其中小王、小张也报了名,则两人都被选中且被分在不同组的概率为______ .
您最近半年使用:0次
5 . 下列说法正确的是( )
A.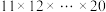 可表示为 可表示为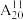 |
| B.5个朋友聚会,见面后每两人握手一次,一共握手10次 |
| C.若把英语单词“happy”的字母顺序写错,则可能出现的错误共有59种 |
| D.将4名老师分派到两个学校支教,每个学校至少派1人,则共有8种不同的分派方法 |
您最近半年使用:0次
6 . 2023年3月5号是毛泽东主席提出“向雷锋同志学习”60周年纪念日,某志愿者服务队在该日安排4位志愿者到两所敬老院开展志愿服务活动,要求每所敬老院至少安排1人,每个志愿者都要参加活动,则不同的分配方法数是( )
| A.8 | B.12 | C.14 | D.20 |
您最近半年使用:0次
7 . 将甲、乙等5位同学分别保送到北京大学、上海交通大学、浙江大学三所大学就读,则每所大学至少保送一人的不同保送方法有( )
| A.240种 | B.180种 |
| C.150种 | D.540种 |
您最近半年使用:0次
8 . 按下列要求分配6本不同的书.
(1)分成三份,1份1本,1份2本,1份3本,有___________ 种不同的分配方式;
(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本,有___________ 种不同的分配方式;
(3)平均分成三份,每份2本,有___________ 种不同的分配方式;
(4)平均分配给甲、乙、丙三人,每人2本,有___________ 种不同的分配方式;
(5)分成三份,1份4本,另外两份每份1本,有___________ 种不同的分配方式;
(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本,有___________ 种不同的分配方式;
(7)甲得1本,乙得1本,丙得4本,有___________ 种不同的分配方式.
(1)分成三份,1份1本,1份2本,1份3本,有
(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本,有
(3)平均分成三份,每份2本,有
(4)平均分配给甲、乙、丙三人,每人2本,有
(5)分成三份,1份4本,另外两份每份1本,有
(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本,有
(7)甲得1本,乙得1本,丙得4本,有
您最近半年使用:0次
9 . 将9名大学生志愿者安排在星期五、星期六及星期日3天参加社区公益活动,每天分别安排3人,每人参加一次,则不同的安排方案共有________ 种.(用数字作答)
您最近半年使用:0次



