1 . 数列 的前n项和为
的前n项和为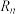 ,记
,记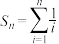 ,数列
,数列 满足
满足 ,
,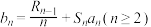 ,且数列
,且数列 的前n项和为
的前n项和为 .
.
(1)请写出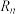 ,
, ,
, 满足的关系式,并加以证明;
满足的关系式,并加以证明;
(2)若数列 通项公式为
通项公式为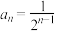 ,证明:
,证明: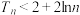 .
.
 的前n项和为
的前n项和为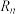 ,记
,记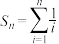 ,数列
,数列 满足
满足 ,
,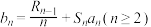 ,且数列
,且数列 的前n项和为
的前n项和为 .
.(1)请写出
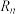 ,
, ,
, 满足的关系式,并加以证明;
满足的关系式,并加以证明;(2)若数列
 通项公式为
通项公式为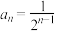 ,证明:
,证明: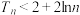 .
.
您最近半年使用:0次
2 . 若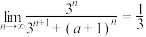 (
(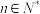 ),则实数a满足( )
),则实数a满足( )
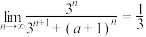 (
(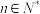 ),则实数a满足( )
),则实数a满足( )A. | B. |
C.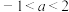 | D.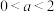 |
您最近半年使用:0次
3 . 在数列 中,
中, ,
,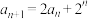 .
.
(1)设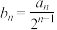 (
(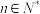 ),证明:数列
),证明:数列 是等差数列;
是等差数列;
(2)设数列 的前n项和
的前n项和 ,求
,求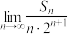 的值;
的值;
(3)设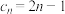 ,数列
,数列 的前n项和为
的前n项和为 ,
, ,是否存在实数t,使得对任意的正整数n和实数
,是否存在实数t,使得对任意的正整数n和实数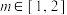 ,都有
,都有 成立?请说明理由.
成立?请说明理由.
 中,
中, ,
,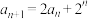 .
.(1)设
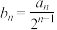 (
(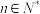 ),证明:数列
),证明:数列 是等差数列;
是等差数列;(2)设数列
 的前n项和
的前n项和 ,求
,求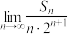 的值;
的值;(3)设
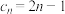 ,数列
,数列 的前n项和为
的前n项和为 ,
, ,是否存在实数t,使得对任意的正整数n和实数
,是否存在实数t,使得对任意的正整数n和实数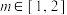 ,都有
,都有 成立?请说明理由.
成立?请说明理由.
您最近半年使用:0次
4 . Sierpinski三角形是一种分形图形,它的构造方法如下图所示:把边长为1的等边三角形分成四等份,挖掉中间那一份,然后继续对另外三个三角形进行这样的操作,并且无限地进行下去,并且将下图依次记为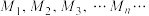

(1)求 中黑色三角形的个数
中黑色三角形的个数 和白色三角形的个数
和白色三角形的个数 ;
;
(2)求 中黑色三角形的周长
中黑色三角形的周长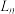 和面积
和面积 ;
;
(3)求黑色三角形面积的极限.

(1)求
 中黑色三角形的个数
中黑色三角形的个数 和白色三角形的个数
和白色三角形的个数 ;
;(2)求
 中黑色三角形的周长
中黑色三角形的周长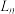 和面积
和面积 ;
;(3)求黑色三角形面积的极限.
您最近半年使用:0次
5 . 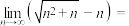
______
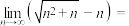
您最近半年使用:0次
6 . 若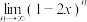 存在,则实数x的取值范围为
存在,则实数x的取值范围为________
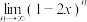 存在,则实数x的取值范围为
存在,则实数x的取值范围为
您最近半年使用:0次
2020-02-11更新
|
95次组卷
|
3卷引用:上海市新川中学2016-2017学年高二上学期9月月考数学试题
7 . 计算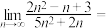
______
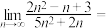
您最近半年使用:0次
8 . 若不等式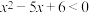 的解集为
的解集为 ,则
,则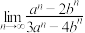 =
=_________ .
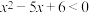 的解集为
的解集为 ,则
,则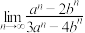 =
=
您最近半年使用:0次
2020-02-10更新
|
42次组卷
|
2卷引用:2016届上海市徐汇区、金山区、松江区高考二模(文科)数学试题
9 . 计算: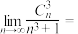
______ ;
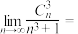
您最近半年使用:0次
2020-02-08更新
|
184次组卷
|
2卷引用:2006 年普通高等学校招生考试数学(理)试题(上海卷)
10 . (1)当n= 1,2,3,10,100,1000,10000,100000,……时,用计算工具计算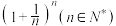 的值;
的值;
(2)当n越来越大时, 的底数越来越小,而指数越来越大,那么
的底数越来越小,而指数越来越大,那么 是否也会越来越大?有没有最大值?
是否也会越来越大?有没有最大值?
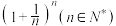 的值;
的值;(2)当n越来越大时,
 的底数越来越小,而指数越来越大,那么
的底数越来越小,而指数越来越大,那么 是否也会越来越大?有没有最大值?
是否也会越来越大?有没有最大值?
您最近半年使用:0次
2020-02-07更新
|
977次组卷
|
5卷引用:人教A版(2019) 必修第一册 逆袭之路 第四章 4.1 指数 小结
人教A版(2019) 必修第一册 逆袭之路 第四章 4.1 指数 小结(已下线)第二章+基本初等函数(Ⅰ)(基础过关)-2020-2021学年高一数学单元测试定心卷(人教A版必修1)人教A版(2019) 必修第一册 新高考名师导学 第四章 4.1 指数(已下线)4.1 指数人教A版(2019)必修第一册课本习题 习题4.1



