1 . 已知函数 及其导函数
及其导函数 的定义域均为
的定义域均为 ,若
,若 是奇函数,
是奇函数,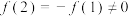 ,且对任意
,且对任意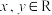 ,
,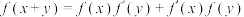 ,则( )
,则( )
 及其导函数
及其导函数 的定义域均为
的定义域均为 ,若
,若 是奇函数,
是奇函数,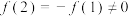 ,且对任意
,且对任意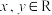 ,
,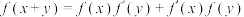 ,则( )
,则( )A.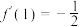 | B.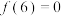 |
C. | D.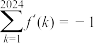 |
您最近半年使用:0次
名校
解题方法
2 . 已知函数 为定义在
为定义在 上的单调连续函数,
上的单调连续函数, ,函数
,函数 ,有以下两个命题:①存在函数
,有以下两个命题:①存在函数 使得
使得 为函数
为函数 的极大值点:②若
的极大值点:②若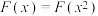 对任意
对任意 恒成立,则
恒成立,则 :则( )
:则( )
 为定义在
为定义在 上的单调连续函数,
上的单调连续函数, ,函数
,函数 ,有以下两个命题:①存在函数
,有以下两个命题:①存在函数 使得
使得 为函数
为函数 的极大值点:②若
的极大值点:②若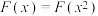 对任意
对任意 恒成立,则
恒成立,则 :则( )
:则( )| A.①为真命题,②为真命题 | B.①为真命题,②为假命题 |
| C.①为假命题,②为真命题 | D.①为假命题,②为假命题 |
您最近半年使用:0次
名校
解题方法
3 . 已知直线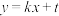 与函数
与函数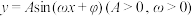 的图象恰有两个切点,设满足条件的k所有可能取值中最大的两个值分别为
的图象恰有两个切点,设满足条件的k所有可能取值中最大的两个值分别为 和
和 ,且
,且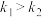 ,则( )
,则( )
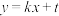 与函数
与函数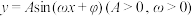 的图象恰有两个切点,设满足条件的k所有可能取值中最大的两个值分别为
的图象恰有两个切点,设满足条件的k所有可能取值中最大的两个值分别为 和
和 ,且
,且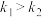 ,则( )
,则( )A.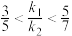 | B. | C. | D.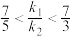 |
您最近半年使用:0次
名校
解题方法
4 . 已知直线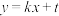 与函数
与函数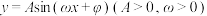 的图象恰有两个切点,设满足条件的
的图象恰有两个切点,设满足条件的 所有可能取值中最大的两个值分别为
所有可能取值中最大的两个值分别为 和
和 ,且
,且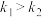 ,则( )
,则( )
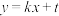 与函数
与函数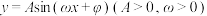 的图象恰有两个切点,设满足条件的
的图象恰有两个切点,设满足条件的 所有可能取值中最大的两个值分别为
所有可能取值中最大的两个值分别为 和
和 ,且
,且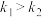 ,则( )
,则( )A.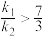 | B. | C. | D.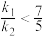 |
您最近半年使用:0次
2023-04-13更新
|
3640次组卷
|
5卷引用:湖北省武汉市2023届高三下学期四月调研数学试题
湖北省武汉市2023届高三下学期四月调研数学试题(已下线)模块六 专题3 易错题目重组卷(湖北卷)(已下线)专题05 三角函数-1广东省肇庆市肇庆中学2023届高三下学期4月月考数学试题(已下线)压轴小题15 三角函数的切线问题
5 . 已知函数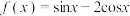 ,则
,则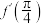 的值为( )
的值为( )
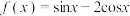 ,则
,则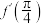 的值为( )
的值为( )A. | B.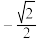 | C. | D.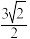 |
您最近半年使用:0次
2023-03-27更新
|
691次组卷
|
3卷引用:河南省新未来2022-2023学年高二下学期3月联考数学试题
名校
解题方法
6 . 若已知函数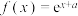 ,
,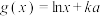 ,
,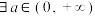 ,若函数
,若函数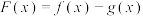 存在零点(参考数据
存在零点(参考数据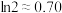 ),则
),则 的取值范围充分不必要条件为( )
的取值范围充分不必要条件为( )
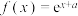 ,
,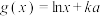 ,
,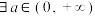 ,若函数
,若函数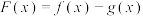 存在零点(参考数据
存在零点(参考数据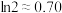 ),则
),则 的取值范围充分不必要条件为( )
的取值范围充分不必要条件为( )A.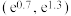 | B.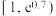 |
C.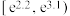 | D.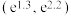 |
您最近半年使用:0次
名校
解题方法
7 . 设函数 图像上不同两点
图像上不同两点 ,
, 处的切线的斜率分别是
处的切线的斜率分别是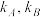 ,规定
,规定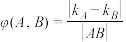 ,(
,( 为线段
为线段 的长度)称为曲线
的长度)称为曲线 在点
在点 与点
与点 之间的“弯曲度”,给出以下命题,其中所有真命题的序号为
之间的“弯曲度”,给出以下命题,其中所有真命题的序号为 __ .
①函数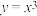 图像上两点
图像上两点 与
与 的横坐标分别为1和
的横坐标分别为1和 ,则
,则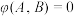 ;
;
②存在这样的函数,其图像上任意不同两点之间的“弯曲度”为常数;
③ ,
, 是抛物线
是抛物线 上任意不同的两点,都有
上任意不同的两点,都有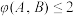 ;
;
④曲线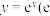 是自然对数的底数)上存在不同的两点
是自然对数的底数)上存在不同的两点 ,
, ,使
,使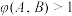 .
.
 图像上不同两点
图像上不同两点 ,
, 处的切线的斜率分别是
处的切线的斜率分别是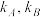 ,规定
,规定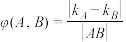 ,(
,( 为线段
为线段 的长度)称为曲线
的长度)称为曲线 在点
在点 与点
与点 之间的“弯曲度”,给出以下命题,其中所有真命题的序号为
之间的“弯曲度”,给出以下命题,其中所有真命题的序号为 ①函数
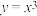 图像上两点
图像上两点 与
与 的横坐标分别为1和
的横坐标分别为1和 ,则
,则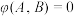 ;
;②存在这样的函数,其图像上任意不同两点之间的“弯曲度”为常数;
③
 ,
, 是抛物线
是抛物线 上任意不同的两点,都有
上任意不同的两点,都有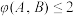 ;
;④曲线
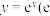 是自然对数的底数)上存在不同的两点
是自然对数的底数)上存在不同的两点 ,
, ,使
,使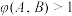 .
.
您最近半年使用:0次
真题
解题方法
8 . 设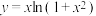 ,求
,求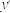 .
.
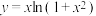 ,求
,求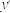 .
.
您最近半年使用:0次
9 . 记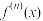 为函数
为函数 的
的 阶导数且
阶导数且 ,
, 若
若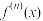 存在,则称
存在,则称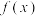
 阶可导.英国数学家泰勒发现:若
阶可导.英国数学家泰勒发现:若 在
在 附近
附近 阶可导,则可构造
阶可导,则可构造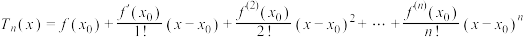 (称为
(称为 次泰勒多项式)来逼近
次泰勒多项式)来逼近 在
在 附近的函数值.据此计算
附近的函数值.据此计算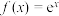 在
在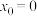 处的3次泰勒多项式为
处的3次泰勒多项式为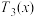 =
=_________ ; 在
在 处的10次泰勒多项式中
处的10次泰勒多项式中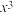 的系数为
的系数为_________
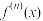 为函数
为函数 的
的 阶导数且
阶导数且 ,
, 若
若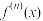 存在,则称
存在,则称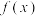
 阶可导.英国数学家泰勒发现:若
阶可导.英国数学家泰勒发现:若 在
在 附近
附近 阶可导,则可构造
阶可导,则可构造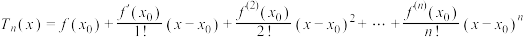 (称为
(称为 次泰勒多项式)来逼近
次泰勒多项式)来逼近 在
在 附近的函数值.据此计算
附近的函数值.据此计算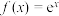 在
在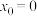 处的3次泰勒多项式为
处的3次泰勒多项式为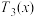 =
= 在
在 处的10次泰勒多项式中
处的10次泰勒多项式中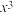 的系数为
的系数为
您最近半年使用:0次
2022-06-11更新
|
1928次组卷
|
4卷引用:广东省深圳市光明区高级中学等2022届高三下学期名校联考数学试题
广东省深圳市光明区高级中学等2022届高三下学期名校联考数学试题(已下线)专题6 “高数衔接”类型江苏省南京市宁海中学2022-2023学年高三下学期二月检测数学试题(已下线)第十章 导数与数学文化 微点2 导数与数学文化(二)
名校
解题方法
10 . 定义:若函数 在
在 上可导,即
上可导,即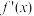 存在,且导函数
存在,且导函数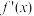 在
在 上也可导则称
上也可导则称 在
在 上存在二阶导函数记
上存在二阶导函数记 ,若
,若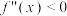 在
在 上恒成立,则称
上恒成立,则称 在
在 上为“凸函数”.①
上为“凸函数”.① ;②
;② ;③
;③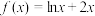 ;④
;④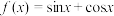 ;这四个函数在
;这四个函数在 上为“凸函数”的有( )
上为“凸函数”的有( )
 在
在 上可导,即
上可导,即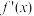 存在,且导函数
存在,且导函数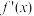 在
在 上也可导则称
上也可导则称 在
在 上存在二阶导函数记
上存在二阶导函数记 ,若
,若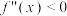 在
在 上恒成立,则称
上恒成立,则称 在
在 上为“凸函数”.①
上为“凸函数”.① ;②
;② ;③
;③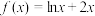 ;④
;④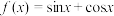 ;这四个函数在
;这四个函数在 上为“凸函数”的有( )
上为“凸函数”的有( )| A.1个 | B.2个 | C.3个 | D.4个 |
您最近半年使用:0次



