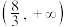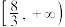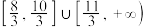解题方法
1 . 函数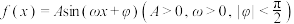 的部分图象如图所示.
的部分图象如图所示. 的解析式;
的解析式;
(2)先将函数 保持横坐标不变,纵坐标变为原来的
保持横坐标不变,纵坐标变为原来的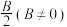 倍,再将图象向左平移
倍,再将图象向左平移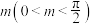 个单位,得到的函数
个单位,得到的函数 为偶函数.若对任意的
为偶函数.若对任意的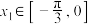 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
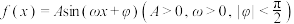 的部分图象如图所示.
的部分图象如图所示.
 的解析式;
的解析式;(2)先将函数
 保持横坐标不变,纵坐标变为原来的
保持横坐标不变,纵坐标变为原来的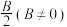 倍,再将图象向左平移
倍,再将图象向左平移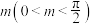 个单位,得到的函数
个单位,得到的函数 为偶函数.若对任意的
为偶函数.若对任意的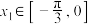 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
名校
解题方法
2 . 设函数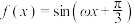 在区间
在区间 恰有三个取得最值的点、两个零点,则实数
恰有三个取得最值的点、两个零点,则实数 的取值范围是( ).
的取值范围是( ).
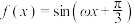 在区间
在区间 恰有三个取得最值的点、两个零点,则实数
恰有三个取得最值的点、两个零点,则实数 的取值范围是( ).
的取值范围是( ).A.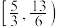 | B.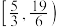 |
C.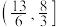 | D.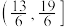 |
您最近半年使用:0次
名校
解题方法
3 . 已知函数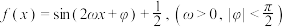 的图象关于直线
的图象关于直线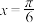 对称.其最小正周期与函数
对称.其最小正周期与函数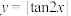 相同.
相同.
(1)求 的对称中心,
的对称中心,
(2)若函数 在
在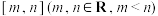 上恰有8个零点,求
上恰有8个零点,求 的最小值;
的最小值;
(3)设函数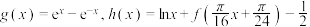 ,证明:
,证明: 有且只有一个零点
有且只有一个零点 ,且
,且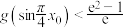 .
.
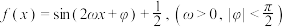 的图象关于直线
的图象关于直线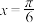 对称.其最小正周期与函数
对称.其最小正周期与函数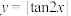 相同.
相同.(1)求
 的对称中心,
的对称中心,(2)若函数
 在
在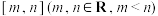 上恰有8个零点,求
上恰有8个零点,求 的最小值;
的最小值;(3)设函数
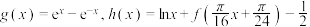 ,证明:
,证明: 有且只有一个零点
有且只有一个零点 ,且
,且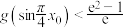 .
.
您最近半年使用:0次
4 . 湖光岩玛珥湖,位于广东省湛江市麻章区湖光镇,是中国乃至世界最大的湿玛珥湖,是中国玛珥湖研究的始发点,也是世界玛玶湖研究的关键点.某小组计划测量如图所示的湖光岩玛珥湖的东西方向的总湖长,即测量湖光岩玛珥湖湖岸的两个测量基点 之间的距离,现在湖光岩玛珥湖的湖岸取另外两个测量基点
之间的距离,现在湖光岩玛珥湖的湖岸取另外两个测量基点 ,测得
,测得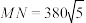 米,
米,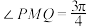 ,
,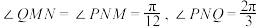 ,则( )
,则( )
 之间的距离,现在湖光岩玛珥湖的湖岸取另外两个测量基点
之间的距离,现在湖光岩玛珥湖的湖岸取另外两个测量基点 ,测得
,测得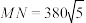 米,
米,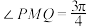 ,
,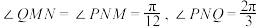 ,则( )
,则( )
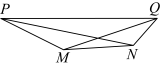
A.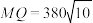 米 米 | B.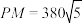 米 米 |
C.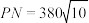 米 米 | D. 米 米 |
您最近半年使用:0次
解题方法
5 . 已知函数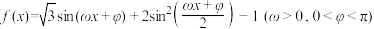 为奇函数,且
为奇函数,且 图象的相邻两对称轴间的距离为
图象的相邻两对称轴间的距离为 .
.
(1)当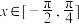 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)将函数 的图象向右平移
的图象向右平移 个单位长度,再把横坐标缩小为原来的
个单位长度,再把横坐标缩小为原来的 (纵坐标变),得到函数
(纵坐标变),得到函数 的图象,当
的图象,当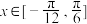 时,求函数
时,求函数 的值域.
的值域.
(3)对于第(2)问中的函数 ,记方程
,记方程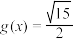 在
在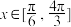 上的根从小到依次为
上的根从小到依次为 ,
, ,……,
,……, ,试确定
,试确定 的值,并求
的值,并求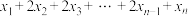 的值.
的值.
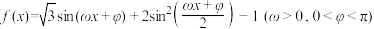 为奇函数,且
为奇函数,且 图象的相邻两对称轴间的距离为
图象的相邻两对称轴间的距离为 .
.(1)当
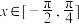 时,求
时,求 的单调递减区间;
的单调递减区间;(2)将函数
 的图象向右平移
的图象向右平移 个单位长度,再把横坐标缩小为原来的
个单位长度,再把横坐标缩小为原来的 (纵坐标变),得到函数
(纵坐标变),得到函数 的图象,当
的图象,当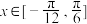 时,求函数
时,求函数 的值域.
的值域.(3)对于第(2)问中的函数
 ,记方程
,记方程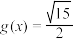 在
在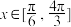 上的根从小到依次为
上的根从小到依次为 ,
, ,……,
,……, ,试确定
,试确定 的值,并求
的值,并求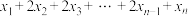 的值.
的值.
您最近半年使用:0次
名校
解题方法
6 . 在 中,
中, ,
, ,
,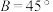 .若利用正弦定理解
.若利用正弦定理解 有两解,则
有两解,则 的取值范围是( )
的取值范围是( )
 中,
中, ,
, ,
,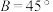 .若利用正弦定理解
.若利用正弦定理解 有两解,则
有两解,则 的取值范围是( )
的取值范围是( )A.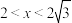 | B.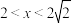 |
C. | D.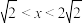 |
您最近半年使用:0次
7 . 求值: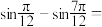
______ .
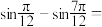
您最近半年使用:0次
解题方法
8 . 在 中,已知
中,已知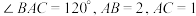 .
.
(1)求边 ;
;
(2)若 为
为 上一点,且
上一点,且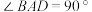 ,求
,求 的面积.
的面积.
 中,已知
中,已知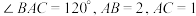 .
.(1)求边
 ;
;(2)若
 为
为 上一点,且
上一点,且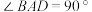 ,求
,求 的面积.
的面积.
您最近半年使用:0次
2024高三·全国·专题练习
解题方法
9 .  中,角
中,角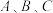 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且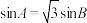 ,则角
,则角
______
 中,角
中,角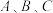 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且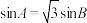 ,则角
,则角
您最近半年使用:0次

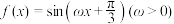 在区间
在区间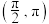 上至少有两个零点,则实数
上至少有两个零点,则实数