1 . 在空间直角坐标系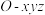 中,若
中,若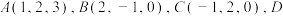 四点可以构成一个平行四边形,则
四点可以构成一个平行四边形,则 的坐标可以为( )
的坐标可以为( )
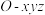 中,若
中,若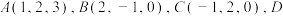 四点可以构成一个平行四边形,则
四点可以构成一个平行四边形,则 的坐标可以为( )
的坐标可以为( )A.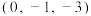 | B.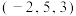 | C.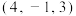 | D. |
您最近半年使用:0次
2023-10-05更新
|
291次组卷
|
7卷引用:河北省邢台市四校质检联盟2023-2024学年高二上学期第一次月考数学试题
河北省邢台市四校质检联盟2023-2024学年高二上学期第一次月考数学试题河北省邢台市河北南宫中学2023-2024学年高二上学期第一次月考数学试题贵州省遵义市2023-2024学年高二上学期10月月考数学试题贵州省普通高中部分学校2023-2024学年高二上学期第一次联考数学试题陕西省西安市昆仑中学2023-2024学年高二上学期10月月考数学试题(已下线)专题01 空间向量与空间位置关系【考题猜想】-2023-2024学年高二数学上学期期中考点大串讲(人教A版2019选择性必修第一册)陕西省咸阳市2023-2024学年高二上学期期末教学质量检测数学试题
名校
解题方法
2 . 下列命题中,正确的有( )
A.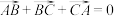 |
B.若平面向量 , , , , 两两的夹角相等,且 两两的夹角相等,且 , ,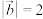 , , ,则 ,则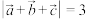 或9 或9 |
C.若平面向量 , , 是一组基底,且存在 是一组基底,且存在 使得 使得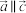 , ,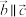 ,则 ,则 |
D.若平面向量 , , 是一组共线向量,则存在 是一组共线向量,则存在 ,使 ,使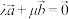 |
您最近半年使用:0次
2023-09-20更新
|
250次组卷
|
2卷引用:河北省邢台市第二中学2022-2023学年高一下学期3月月考数学试题
名校
解题方法
3 . 平面上三个力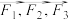 作用于同一点,且处于平衡状态,已知
作用于同一点,且处于平衡状态,已知 ,
, ,
, 与
与 的夹角为45°,则
的夹角为45°,则 的大小为
的大小为_____ N.
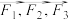 作用于同一点,且处于平衡状态,已知
作用于同一点,且处于平衡状态,已知 ,
, ,
, 与
与 的夹角为45°,则
的夹角为45°,则 的大小为
的大小为
您最近半年使用:0次
解题方法
4 . 在等腰直角 中,
中, ,
, 是
是 的中点,若点
的中点,若点 为线段
为线段 的三等分点,则
的三等分点,则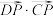 的值可能为( )
的值可能为( )
 中,
中, ,
, 是
是 的中点,若点
的中点,若点 为线段
为线段 的三等分点,则
的三等分点,则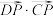 的值可能为( )
的值可能为( )| A.1 | B.2 | C. | D. |
您最近半年使用:0次
解题方法
5 . 已知平面直角坐标系中,等边 的顶点坐标为
的顶点坐标为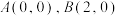 ,点
,点 在第一象限,点
在第一象限,点 是平面内任意一点.
是平面内任意一点.
(1)若 四点能构成一个平行四边形,求点
四点能构成一个平行四边形,求点 的坐标;(写出所有满足条件的情况)
的坐标;(写出所有满足条件的情况)
(2)若点 为线段
为线段 边上一动点(包含
边上一动点(包含 点),求
点),求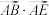 的取值范围.
的取值范围.
 的顶点坐标为
的顶点坐标为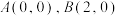 ,点
,点 在第一象限,点
在第一象限,点 是平面内任意一点.
是平面内任意一点.(1)若
 四点能构成一个平行四边形,求点
四点能构成一个平行四边形,求点 的坐标;(写出所有满足条件的情况)
的坐标;(写出所有满足条件的情况)(2)若点
 为线段
为线段 边上一动点(包含
边上一动点(包含 点),求
点),求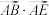 的取值范围.
的取值范围.
您最近半年使用:0次
2023高三·全国·专题练习
6 . 设△ABC外心为O,重心为G.取点H,使 .求证:
.求证:
(1)H是△ABC的垂心;
(2)O,G,H三点共线,且OG:GH=1:2.
 .求证:
.求证:(1)H是△ABC的垂心;
(2)O,G,H三点共线,且OG:GH=1:2.
您最近半年使用:0次
解题方法
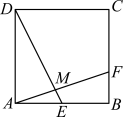
7 . 如图,正方形 的边长为
的边长为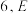 是
是 的中点,
的中点, 是
是 边上靠近点
边上靠近点 的三等分点,
的三等分点, 与
与 交于点
交于点 .
.
(1)求 的余弦值;
的余弦值;
(2)设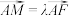 ,求
,求 的值;
的值;
(3)若点 自点A逆时针沿正方形的边再运动到点A,在这个过程中,是否存在这样的点
自点A逆时针沿正方形的边再运动到点A,在这个过程中,是否存在这样的点 ,使得
,使得 ?若存在,求出
?若存在,求出 的长度,若不存在,请说明理由.
的长度,若不存在,请说明理由.
 的边长为
的边长为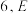 是
是 的中点,
的中点, 是
是 边上靠近点
边上靠近点 的三等分点,
的三等分点, 与
与 交于点
交于点 .
.
(1)求
 的余弦值;
的余弦值;(2)设
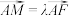 ,求
,求 的值;
的值;(3)若点
 自点A逆时针沿正方形的边再运动到点A,在这个过程中,是否存在这样的点
自点A逆时针沿正方形的边再运动到点A,在这个过程中,是否存在这样的点 ,使得
,使得 ?若存在,求出
?若存在,求出 的长度,若不存在,请说明理由.
的长度,若不存在,请说明理由.
您最近半年使用:0次
名校
解题方法
8 . 已知 ,在直角三角形
,在直角三角形 中,
中,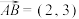 ,
,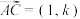 ,则实数
,则实数 的值是
的值是________ .
 ,在直角三角形
,在直角三角形 中,
中,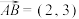 ,
,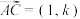 ,则实数
,则实数 的值是
的值是
您最近半年使用:0次
2023-04-21更新
|
325次组卷
|
3卷引用:江苏省镇江市扬中高级中学2022-2023学年高一下学期期中校际联考数学试题
江苏省镇江市扬中高级中学2022-2023学年高一下学期期中校际联考数学试题江苏省镇江第一中学2022-2023学年高二下学期期中校际联考数学试题(已下线)第9章 平面向量 章末题型归纳总结-【帮课堂】(苏教版2019必修第二册)
名校
解题方法
9 . 已知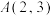 ,
,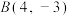 ,点P在直线AB上,且
,点P在直线AB上,且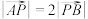 ,求点P的坐标( )
,求点P的坐标( )
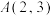 ,
,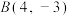 ,点P在直线AB上,且
,点P在直线AB上,且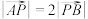 ,求点P的坐标( )
,求点P的坐标( )A.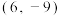 | B.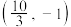 |
C. | D. |
您最近半年使用:0次
2023-04-04更新
|
875次组卷
|
6卷引用:山东省枣庄市滕州市山东省滕州市第一中学2022-2023学年高一下学期3月月考数学试题
山东省枣庄市滕州市山东省滕州市第一中学2022-2023学年高一下学期3月月考数学试题山东省临沂市第一中学文峰校区2022-2023学年高一4月月考数学试题重庆市江津第五中学校2022-2023学年高一下学期期中数学试题四川省宜宾市叙州区第二中学校2022-2023学年高一下学期期中数学试题江西省宜春市丰城市东煌学校2022-2023学年高一下学期期中数学试题(已下线)专题9.5 向量的坐标表示及运算-重难点突破及混淆易错规避(苏教版2019必修第二册)
名校
10 . 已知点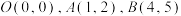 ,且
,且 .
. 试问:
试问:
(1)t为何值时,点P在坐标轴上?
(2)四点O、A、B、P能否成为平行四边形?若能,求出相应的t值,若不能,请说明理由.
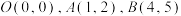 ,且
,且 .
. 试问:
试问:(1)t为何值时,点P在坐标轴上?
(2)四点O、A、B、P能否成为平行四边形?若能,求出相应的t值,若不能,请说明理由.
您最近半年使用:0次
2023-03-28更新
|
209次组卷
|
3卷引用:重庆市辅仁中学校2022-2023学年高一下学期第一次质量检测数学试题
重庆市辅仁中学校2022-2023学年高一下学期第一次质量检测数学试题内蒙古自治区乌兰察布市衡水卓远中学2022-2023学年高一下学期期中数学试题(已下线)6.3.2+6.3.3+6.3.4平面向量的正交分解及坐标表示 【第二课】“上好三节课,做好三套题“高中数学素养晋级之路



