1 . 设数列 的前
的前 项和为
项和为 ,若存在非零常数
,若存在非零常数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有 ,则称数列
,则称数列 具有性质
具有性质 :①存在等差数列
:①存在等差数列 具有性质
具有性质 ;②不存在等比数列
;②不存在等比数列 具有性质
具有性质 ;对于以上两个命题,下列判断正确的是( )
;对于以上两个命题,下列判断正确的是( )
 的前
的前 项和为
项和为 ,若存在非零常数
,若存在非零常数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有 ,则称数列
,则称数列 具有性质
具有性质 :①存在等差数列
:①存在等差数列 具有性质
具有性质 ;②不存在等比数列
;②不存在等比数列 具有性质
具有性质 ;对于以上两个命题,下列判断正确的是( )
;对于以上两个命题,下列判断正确的是( )| A.①真②真 | B.①真②假 | C.①假②真 | D.①假②假 |
您最近半年使用:0次
2 . 已知在平面直角坐标系中有一个点列: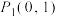 ,
,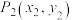 ,…,
,…,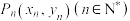 .若点
.若点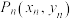 到点
到点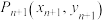 的变化关系为
的变化关系为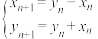 (
( ),则
),则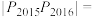
__________ .
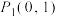 ,
,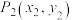 ,…,
,…,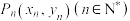 .若点
.若点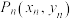 到点
到点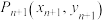 的变化关系为
的变化关系为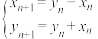 (
( ),则
),则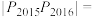
您最近半年使用:0次
3 . 数列 的前n项和为
的前n项和为 ,若数列
,若数列 与函数
与函数 满足:①
满足:① 的定义域为R;②数列
的定义域为R;②数列 与函数
与函数 均单调递增;③
均单调递增;③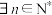 使
使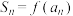 成立,则称数列
成立,则称数列 与函数
与函数 具有“单调偶遇关系”.有下面四个结论:
具有“单调偶遇关系”.有下面四个结论:
(1)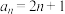 与
与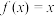 具有“单调偶遇关系”
具有“单调偶遇关系”
(2) 与
与 不具有“单调偶遇关系”
不具有“单调偶遇关系”
(3)与数列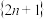 具有“单调偶遇关系的函数有有限个
具有“单调偶遇关系的函数有有限个
(4)与数列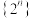 具有“单调偶遇关系”的函数有无数个
具有“单调偶遇关系”的函数有无数个
其中正确结论的序号为__________ .
 的前n项和为
的前n项和为 ,若数列
,若数列 与函数
与函数 满足:①
满足:① 的定义域为R;②数列
的定义域为R;②数列 与函数
与函数 均单调递增;③
均单调递增;③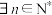 使
使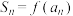 成立,则称数列
成立,则称数列 与函数
与函数 具有“单调偶遇关系”.有下面四个结论:
具有“单调偶遇关系”.有下面四个结论:(1)
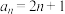 与
与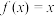 具有“单调偶遇关系”
具有“单调偶遇关系”(2)
 与
与 不具有“单调偶遇关系”
不具有“单调偶遇关系”(3)与数列
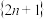 具有“单调偶遇关系的函数有有限个
具有“单调偶遇关系的函数有有限个(4)与数列
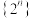 具有“单调偶遇关系”的函数有无数个
具有“单调偶遇关系”的函数有无数个其中正确结论的序号为
您最近半年使用:0次
4 . 以下四个命题,其中满足“假设当 时命题成立,则当
时命题成立,则当 时命题也成立”,但不满足“当
时命题也成立”,但不满足“当 (
(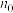 是题中给定的n的初始值)时命题成立”的是( )
是题中给定的n的初始值)时命题成立”的是( )
 时命题成立,则当
时命题成立,则当 时命题也成立”,但不满足“当
时命题也成立”,但不满足“当 (
(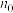 是题中给定的n的初始值)时命题成立”的是( )
是题中给定的n的初始值)时命题成立”的是( )A. |
B. |
C.凸n边形的内角和为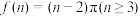 |
D.凸n边形的对角线条数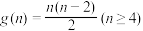 |
您最近半年使用:0次
名校
解题方法
5 . “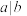 ”表示实数
”表示实数 整除实数
整除实数 ,例如:
,例如: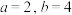 ,已知数列
,已知数列 满足:
满足: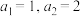 ,若
,若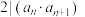 ,则
,则 ,否则
,否则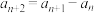 ,那么下列说法正确的有( )
,那么下列说法正确的有( )
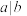 ”表示实数
”表示实数 整除实数
整除实数 ,例如:
,例如: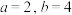 ,已知数列
,已知数列 满足:
满足: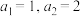 ,若
,若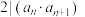 ,则
,则 ,否则
,否则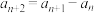 ,那么下列说法正确的有( )
,那么下列说法正确的有( )A. | B.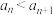 |
C.对任意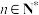 ,都有 ,都有 | D.存在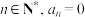 |
您最近半年使用:0次
2024高二·全国·专题练习
解题方法
6 . 意大利数学家列昂那多斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55, ,即
,即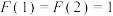 ,
,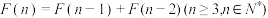 ,此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2除后的余数构成一个新数列
,此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2除后的余数构成一个新数列 ,则数列
,则数列 的前2024项的和为( )
的前2024项的和为( )
 ,即
,即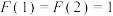 ,
,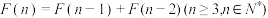 ,此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2除后的余数构成一个新数列
,此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用.若此数列被2除后的余数构成一个新数列 ,则数列
,则数列 的前2024项的和为( )
的前2024项的和为( )| A.1348 | B.675 | C.1349 | D.1350 |
您最近半年使用:0次
2024-03-09更新
|
186次组卷
|
3卷引用:1.5 数学归纳法7种常见考法归类(2)
7 . 已知数列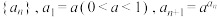 .给出下列四个结论:
.给出下列四个结论:
①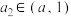 ;
;
②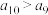 ;
;
③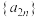 为递增数列;
为递增数列;
④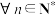 ,使得
,使得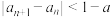 .
.
其中所有正确结论的序号是__________ .
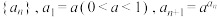 .给出下列四个结论:
.给出下列四个结论:①
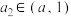 ;
;②
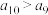 ;
;③
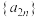 为递增数列;
为递增数列;④
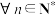 ,使得
,使得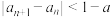 .
.其中所有正确结论的序号是
您最近半年使用:0次
8 . 设函数y=f(x)对任意实数x,y都有f(x+y)=f(x)+f(y)+2xy.
(1)求f(0)的值;
(2)若f(1)=1,求f(2),f(3),f(4)的值;
(3)在(2)的条件下,猜想f(n)(n∈N*)的表达式,并用数学归纳法加以证明.
(1)求f(0)的值;
(2)若f(1)=1,求f(2),f(3),f(4)的值;
(3)在(2)的条件下,猜想f(n)(n∈N*)的表达式,并用数学归纳法加以证明.
您最近半年使用:0次
2023-12-18更新
|
99次组卷
|
12卷引用:2010年本溪市普通高中高二下学期期末考试(理科)数学卷
(已下线)2010年本溪市普通高中高二下学期期末考试(理科)数学卷(已下线)2012-2013学年福建省莆田一中高二下学期第一学段考试理科数学试卷2015-2016学年江苏清江中学高二下期中数学(理)试卷2016-2017河北武邑中学高二上周考9.25理数学试卷安徽省宿州市十三所重点中学2020-2021学年高二下学期期中理科数学试题沪教版(2020) 一轮复习 堂堂清 第四单元 4.4 数列的通项公式(已下线)第五章 数列(A卷·知识通关练)(5)人教B版(2019) 选修第三册 北京名校同步练习册 第五章 数列 5.5 数学归纳法人教A版(2019) 选修第二册 数学奇书 第四章 数列 4.4 数学归纳法(已下线)4.4 数学归纳法(2)(已下线)第五章:数列章末重点题型复习(2)(已下线)1.5数学归纳法(分层练习,7大考点)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)
9 . 写出下列数列的一个通项公式.
(1)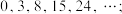
(2)
(3)0,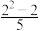 ,
,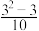 ,
,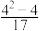 ,…;
,…;
(4)1,11,111,1 111,….
(1)
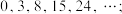
(2)

(3)0,
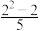 ,
,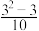 ,
,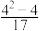 ,…;
,…;(4)1,11,111,1 111,….
您最近半年使用:0次
2023-12-18更新
|
260次组卷
|
5卷引用:人教A版(2019) 选修第二册 数学奇书 第四章 数列 4.1 数列的概念 第1课时 数列的概念与简单表示法
人教A版(2019) 选修第二册 数学奇书 第四章 数列 4.1 数列的概念 第1课时 数列的概念与简单表示法(已下线)5.1.1 数列的概念(3知识点+6题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)(已下线)1.1 数列的概念4种常见考法归类-【帮课堂】2023-2024学年高二数学同步学与练(北师大版2019选择性必修第二册)(已下线)专题15 数列10种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(苏教版2019选择性必修第一册)(已下线)1.1.1 数列的概念(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)
10 . 已知等差数列 公差为
公差为 ,其前
,其前 项和为
项和为 ,等差数列
,等差数列 公差为
公差为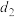 ,其前
,其前 项和为
项和为 ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )
①若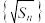 为等差数列,则
为等差数列,则 ②若
②若 为等差数列,则
为等差数列,则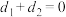
③若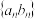 为等差数列,则
为等差数列,则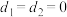 ④若
④若 ,则
,则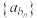 是公差为
是公差为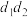 的等差数列.
的等差数列.
 公差为
公差为 ,其前
,其前 项和为
项和为 ,等差数列
,等差数列 公差为
公差为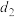 ,其前
,其前 项和为
项和为 ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( ) ①若
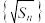 为等差数列,则
为等差数列,则 ②若
②若 为等差数列,则
为等差数列,则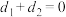
③若
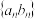 为等差数列,则
为等差数列,则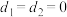 ④若
④若 ,则
,则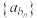 是公差为
是公差为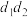 的等差数列.
的等差数列.A. | B. | C. | D. |
您最近半年使用:0次



