名校
解题方法
1 . 若实数a,b,c满足 ,
, ,则下列结论中正确的是( )
,则下列结论中正确的是( )
 ,
, ,则下列结论中正确的是( )
,则下列结论中正确的是( )A. | B. | C.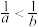 | D.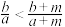 |
您最近半年使用:0次
2024-03-03更新
|
140次组卷
|
2卷引用:河南省济源市2023-2024学年高一上学期期末质量调研数学试题
2 . 已知正数 满足
满足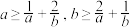 ,则( )
,则( )
 满足
满足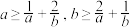 ,则( )
,则( )A.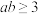 | B.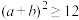 |
C.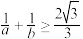 | D.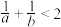 |
您最近半年使用:0次
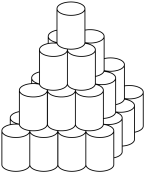
3 . 在商店里,如图分层堆砌易拉罐,最顶层放1个,第二层放4个,第三层放9个.如此下去,第六层放___________ 个.

您最近半年使用:0次
名校
解题方法
4 . 已知 ,
,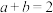 ,则( )
,则( )
 ,
,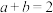 ,则( )
,则( )A. | B. |
C. | D. |
您最近半年使用:0次
解题方法
5 . 如果 ,则下列不等式中一定成立的是( )
,则下列不等式中一定成立的是( )
 ,则下列不等式中一定成立的是( )
,则下列不等式中一定成立的是( )A.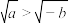 | B.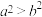 | C. | D.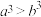 |
您最近半年使用:0次
6 . (1)已知 克糖水中含有
克糖水中含有 克糖(
克糖(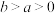 ),再添加
),再添加 克糖(
克糖( )(假设全部溶解),糖水变甜了.请将这一事实表示为一个不等式,不必证明.利用此结论证明:若
)(假设全部溶解),糖水变甜了.请将这一事实表示为一个不等式,不必证明.利用此结论证明:若 为三角形的三边长,则
为三角形的三边长,则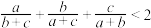 .
.
(2)超市里面提供两种糖:白糖每千克 元,红糖每千克
元,红糖每千克 元
元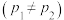 .小东买了相同质量的两种糖,小华买了相同价钱的两种糖.请问谁买的糖的平均价格比较高?请证明你的结论.(物品的平均价格
.小东买了相同质量的两种糖,小华买了相同价钱的两种糖.请问谁买的糖的平均价格比较高?请证明你的结论.(物品的平均价格 物品的总价钱
物品的总价钱 物品的总质量)
物品的总质量)
 克糖水中含有
克糖水中含有 克糖(
克糖(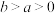 ),再添加
),再添加 克糖(
克糖( )(假设全部溶解),糖水变甜了.请将这一事实表示为一个不等式,不必证明.利用此结论证明:若
)(假设全部溶解),糖水变甜了.请将这一事实表示为一个不等式,不必证明.利用此结论证明:若 为三角形的三边长,则
为三角形的三边长,则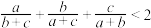 .
.(2)超市里面提供两种糖:白糖每千克
 元,红糖每千克
元,红糖每千克 元
元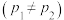 .小东买了相同质量的两种糖,小华买了相同价钱的两种糖.请问谁买的糖的平均价格比较高?请证明你的结论.(物品的平均价格
.小东买了相同质量的两种糖,小华买了相同价钱的两种糖.请问谁买的糖的平均价格比较高?请证明你的结论.(物品的平均价格 物品的总价钱
物品的总价钱 物品的总质量)
物品的总质量)
您最近半年使用:0次
7 . 已知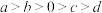 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
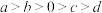 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )A. | B. | C. | D. |
您最近半年使用:0次
8 . 下列命题中,正确的是( )
A.若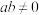 且 且 ,则 ,则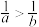 | B.若 ,则 ,则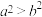 |
C.若 , , ,则 ,则 | D.若 ,则 ,则 |
您最近半年使用:0次
9 . 记 (
( 且
且 )的展开式中含x项的系数为
)的展开式中含x项的系数为 ,含
,含 项的系数为
项的系数为 .
.
(1)求 ;
;
(2)若 ,对
,对 ,3,4成立,求实数a,b,c的值;
,3,4成立,求实数a,b,c的值;
(3)对(2)中的实数a,b,c,证明:对任意 且
且 ,
, 都成立.
都成立.
 (
( 且
且 )的展开式中含x项的系数为
)的展开式中含x项的系数为 ,含
,含 项的系数为
项的系数为 .
.(1)求
 ;
;(2)若
 ,对
,对 ,3,4成立,求实数a,b,c的值;
,3,4成立,求实数a,b,c的值;(3)对(2)中的实数a,b,c,证明:对任意
 且
且 ,
, 都成立.
都成立.
您最近半年使用:0次
2023-11-01更新
|
184次组卷
|
7卷引用:江苏省常州2018届高三上学期期末数学(理)
江苏省常州2018届高三上学期期末数学(理)专题20 数学归纳法及其证明-《巅峰冲刺2020年高考之二轮专项提升》[江苏]2020届江苏省南通市如皋中学高三下学期3月线上模拟考试数学试题(已下线)专题07 计数原理-2020-2021学年高二数学下学期期末专项复习(北师大版2019选择性必修第一册、第二册)四川省雅安市天立学校2022-2023学年高二下学期第一次月考数学(理)试题上海市复旦中学2023-2024学年高二上学期期末考试数学试卷(已下线)第六章 计数原理(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)
10 . 已知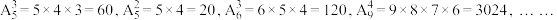 ,观察并找规律,计算
,观察并找规律,计算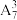 的结果是( )
的结果是( )
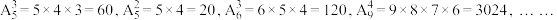 ,观察并找规律,计算
,观察并找规律,计算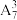 的结果是( )
的结果是( )| A.42 | B.120 | C.210 | D.840 |
您最近半年使用:0次



