名校
解题方法
1 . 图,四边形 的斜二测画法直观图为等腰梯形
的斜二测画法直观图为等腰梯形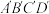 .已知
.已知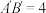 ,
,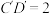 ,则下列说法正确的是( )
,则下列说法正确的是( )
 的斜二测画法直观图为等腰梯形
的斜二测画法直观图为等腰梯形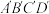 .已知
.已知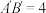 ,
,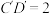 ,则下列说法正确的是( )
,则下列说法正确的是( )
A. | B. |
C.四边形 的周长为 的周长为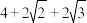 | D.四边形 的面积为 的面积为 |
您最近半年使用:0次
昨日更新
|
1120次组卷
|
16卷引用:湖北省武汉市部分重点中学2022-2023学年高一下学期期中联考数学试题
湖北省武汉市部分重点中学2022-2023学年高一下学期期中联考数学试题(已下线)第八章:立体几何初步 重点题型复习(1)第八章 立体几何初步(单元测试)-【同步题型讲义】山东省聊城市聊城第四中学2022-2023学年高一下学期5月月考数学试题安徽省滁州中学2022-2023学年高一下学期数学周测试卷(第12次)(已下线)河南省南阳市2022-2023学年高一下学期期末数学试题贵州省黔西南布依族苗族自治州兴义第一中学2022-2023学年高一下学期第三次月考数学试题(已下线)高一下学期第二次月考卷(测试范围:第6~9章平面向量、复数、立体几何、统计)(已下线)专题8.2 立体图形的直观图-举一反三系列(人教A版2019必修第二册)上海市浦东复旦附中分校2023-2024学年高三下学期3月月考数学试题(已下线)8.2立体图形的直观图(已下线)专题14 立体图形的直观图-《重难点题型·高分突破》(人教A版2019必修第二册)重庆市长寿中学校2023-2024学年高一下学期学段考试一(4月)试题(已下线)专题16 直观图的斜二测画法-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)8.2立体图形的直观图--随堂检测(已下线)专题13.1基本立体图形-重难点突破及混淆易错规避(苏教版2019必修第二册)
2024·全国·模拟预测
解题方法
2 . 已知正方体 的棱长为2,点
的棱长为2,点 为平面
为平面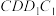 上一动点,则( )
上一动点,则( )
 的棱长为2,点
的棱长为2,点 为平面
为平面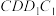 上一动点,则( )
上一动点,则( )A.当点 为 为 的中点时,直线 的中点时,直线 与 与 所成角的余弦值为 所成角的余弦值为 |
B.当点 在棱 在棱 上时, 上时,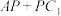 的最小值为 的最小值为 |
C.当点 在正方形 在正方形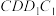 内时,若 内时,若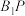 与平面 与平面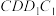 所成的角为 所成的角为 ,则点 ,则点 的轨迹长度为 的轨迹长度为 |
D.当点 在棱 在棱 (不含顶点)上时,平面 (不含顶点)上时,平面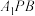 截此正方体所得的截面为梯形 截此正方体所得的截面为梯形 |
您最近半年使用:0次
2024·全国·模拟预测
3 . 如图,在四棱锥 中,
中,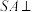 平面
平面 ,底面
,底面 是正方形,且
是正方形,且 4,点
4,点 为
为 的中点,点
的中点,点 满足
满足 ,平面
,平面 交
交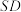 于点
于点 ,则下列说法正确的是( )
,则下列说法正确的是( )
 中,
中,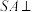 平面
平面 ,底面
,底面 是正方形,且
是正方形,且 4,点
4,点 为
为 的中点,点
的中点,点 满足
满足 ,平面
,平面 交
交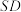 于点
于点 ,则下列说法正确的是( )
,则下列说法正确的是( )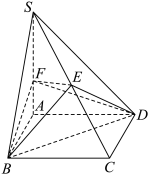
A. 的最小值为 的最小值为 |
B.三棱锥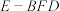 的体积不变 的体积不变 |
C.若 ,则 ,则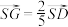 |
D.若 ,则四边形 ,则四边形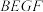 的面积为 的面积为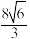 |
您最近半年使用:0次
名校
解题方法
4 . 下列物体,能够被整体放入长、宽、高分别为2,1,1(单位:m)的长方体容器(容器壁厚度忽略不计)内的有( )
| A.半径为0.6m的球体 |
| B.一组相对棱为1.4m,其余棱都为2m的四面体 |
| C.底面半径为0.005m,高为2.5m的圆柱体 |
| D.底面半径为0.6m,高为0.005m的圆柱体 |
您最近半年使用:0次
5 . 已知球 是棱长为2的正方体
是棱长为2的正方体 的内切球,
的内切球, 是
是 的中点,
的中点, 是
是 的中点,
的中点, 是球
是球 的球面上任意一点,则下列说法正确的是( )
的球面上任意一点,则下列说法正确的是( )
 是棱长为2的正方体
是棱长为2的正方体 的内切球,
的内切球, 是
是 的中点,
的中点, 是
是 的中点,
的中点, 是球
是球 的球面上任意一点,则下列说法正确的是( )
的球面上任意一点,则下列说法正确的是( )A.若 ,则动点 ,则动点 的轨迹长度为 的轨迹长度为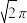 |
B.三棱锥 的体积的最大值为 的体积的最大值为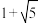 |
C.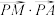 的取值范围是 的取值范围是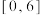 |
D.若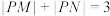 ,则 ,则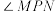 的大小为定值 的大小为定值 |
您最近半年使用:0次
6 . 在三棱锥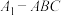 中,
中,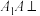 平面
平面 ,
,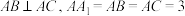 ,P为
,P为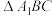 内的一个动点(包括边界),
内的一个动点(包括边界), 与平面
与平面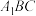 所成的角为
所成的角为 ,则( )
,则( )
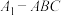 中,
中,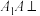 平面
平面 ,
,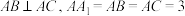 ,P为
,P为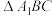 内的一个动点(包括边界),
内的一个动点(包括边界), 与平面
与平面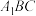 所成的角为
所成的角为 ,则( )
,则( )A.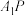 的最小值为 的最小值为 | B.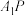 的最大值为 的最大值为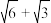 |
C.有且仅有一个点P,使得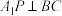 | D.所有满足条件的线段 形成的曲面面积 形成的曲面面积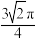 |
您最近半年使用:0次
解题方法
7 . 平行六面体 中,
中, 为
为 的中点,设
的中点,设 ,
, ,
,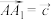 ,用
,用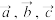 表示
表示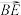 ,则( )
,则( )
 中,
中, 为
为 的中点,设
的中点,设 ,
, ,
,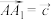 ,用
,用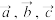 表示
表示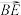 ,则( )
,则( )A.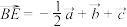 | B.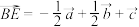 |
C.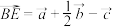 | D.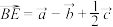 |
您最近半年使用:0次
名校
解题方法
8 . 正三棱锥 中,底面边长
中,底面边长 ,侧棱
,侧棱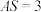 ,向量
,向量 ,
, 满足
满足 ,
,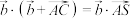 ,则
,则 的最大值为
的最大值为____________ .
 中,底面边长
中,底面边长 ,侧棱
,侧棱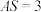 ,向量
,向量 ,
, 满足
满足 ,
,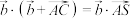 ,则
,则 的最大值为
的最大值为
您最近半年使用:0次
2024-04-15更新
|
500次组卷
|
3卷引用:上海市浦东新区2024届高三下学期期中教学质量检测数学试卷
2024·全国·模拟预测
解题方法
9 . 在三棱锥 中,底面
中,底面 是等边三角形,侧面
是等边三角形,侧面 是等腰直角三角形,
是等腰直角三角形,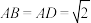 ,
, 是平面
是平面 内一点,且
内一点,且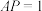 ,若
,若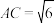 ,则点
,则点 的轨迹长度为( )
的轨迹长度为( )
 中,底面
中,底面 是等边三角形,侧面
是等边三角形,侧面 是等腰直角三角形,
是等腰直角三角形,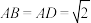 ,
, 是平面
是平面 内一点,且
内一点,且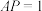 ,若
,若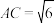 ,则点
,则点 的轨迹长度为( )
的轨迹长度为( )A. | B. | C.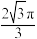 | D. |
您最近半年使用:0次
2024高三·全国·专题练习
解题方法
10 . 正三棱台 中,下底面的边长为a,侧棱与底面成角60°,过AB作截面垂直于
中,下底面的边长为a,侧棱与底面成角60°,过AB作截面垂直于 ,求截面面积.
,求截面面积.
 中,下底面的边长为a,侧棱与底面成角60°,过AB作截面垂直于
中,下底面的边长为a,侧棱与底面成角60°,过AB作截面垂直于 ,求截面面积.
,求截面面积.
您最近半年使用:0次



