2024·全国·模拟预测
1 . 已知双曲线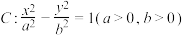 的左、右焦点分别为
的左、右焦点分别为 ,第一象限内的点
,第一象限内的点 在
在 上,点
上,点 关于坐标原点的对称点为
关于坐标原点的对称点为 ,点
,点 在
在 内且到
内且到 三边的距离相等.若点
三边的距离相等.若点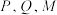 在
在 轴上的射影分别为
轴上的射影分别为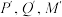 ,
,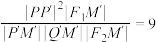 ,则
,则 的离心率为( )
的离心率为( )
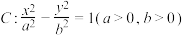 的左、右焦点分别为
的左、右焦点分别为 ,第一象限内的点
,第一象限内的点 在
在 上,点
上,点 关于坐标原点的对称点为
关于坐标原点的对称点为 ,点
,点 在
在 内且到
内且到 三边的距离相等.若点
三边的距离相等.若点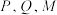 在
在 轴上的射影分别为
轴上的射影分别为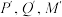 ,
,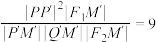 ,则
,则 的离心率为( )
的离心率为( )| A.2 | B.8 | C. | D.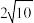 |
您最近半年使用:0次
2024·全国·模拟预测
2 . 已知过抛物线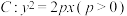 的焦点F的直线与C交于A,B两点,线段AB的中点为
的焦点F的直线与C交于A,B两点,线段AB的中点为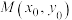 ,且
,且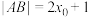 ,
,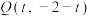 ,若点P在抛物线C上,则
,若点P在抛物线C上,则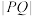 的最小值为
的最小值为______ .
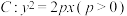 的焦点F的直线与C交于A,B两点,线段AB的中点为
的焦点F的直线与C交于A,B两点,线段AB的中点为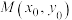 ,且
,且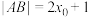 ,
,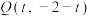 ,若点P在抛物线C上,则
,若点P在抛物线C上,则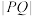 的最小值为
的最小值为
您最近半年使用:0次
2024·全国·模拟预测
解题方法
3 . 已知 为坐标原点,圆
为坐标原点,圆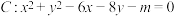 上恰好有两个点到点
上恰好有两个点到点 的距离为1,则实数
的距离为1,则实数 的取值范围为
的取值范围为______ .
 为坐标原点,圆
为坐标原点,圆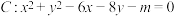 上恰好有两个点到点
上恰好有两个点到点 的距离为1,则实数
的距离为1,则实数 的取值范围为
的取值范围为
您最近半年使用:0次
解题方法
4 . 已知实数 满足
满足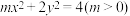 ,若
,若 的最大值为4,则
的最大值为4,则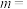 ( )
( )
 满足
满足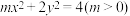 ,若
,若 的最大值为4,则
的最大值为4,则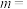 ( )
( )A. | B. | C. | D. |
您最近半年使用:0次
解题方法
5 . 已知椭圆 的短轴上端点为P,过点P作椭圆互相垂直的两弦
的短轴上端点为P,过点P作椭圆互相垂直的两弦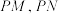 .连接
.连接 ,试求点P在
,试求点P在 上的射影Q的轨迹方程.
上的射影Q的轨迹方程.
 的短轴上端点为P,过点P作椭圆互相垂直的两弦
的短轴上端点为P,过点P作椭圆互相垂直的两弦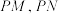 .连接
.连接 ,试求点P在
,试求点P在 上的射影Q的轨迹方程.
上的射影Q的轨迹方程.
您最近半年使用:0次
23-24高二上·全国·课后作业
名校
解题方法
6 . 已知圆系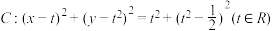 ,圆
,圆 过
过 轴上的定点
轴上的定点 ,线段
,线段 是圆
是圆 在
在 轴上截得的弦,设
轴上截得的弦,设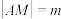 ,
,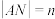 .对于下列命题:
.对于下列命题:
①不论 取何实数,圆心
取何实数,圆心 始终落在曲线
始终落在曲线 上;
上;
②不论 取何实数,弦
取何实数,弦 的长为定值1;
的长为定值1;
③不论 取何实数,圆系
取何实数,圆系 的所有圆都与直线
的所有圆都与直线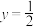 相切;
相切;
④式子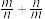 的取值范围是
的取值范围是 .
.
其中真命题的序号是________ (把所有真命题的序号都填上)
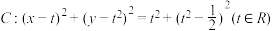 ,圆
,圆 过
过 轴上的定点
轴上的定点 ,线段
,线段 是圆
是圆 在
在 轴上截得的弦,设
轴上截得的弦,设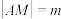 ,
,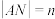 .对于下列命题:
.对于下列命题:①不论
 取何实数,圆心
取何实数,圆心 始终落在曲线
始终落在曲线 上;
上;②不论
 取何实数,弦
取何实数,弦 的长为定值1;
的长为定值1;③不论
 取何实数,圆系
取何实数,圆系 的所有圆都与直线
的所有圆都与直线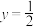 相切;
相切;④式子
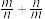 的取值范围是
的取值范围是 .
.其中真命题的序号是
您最近半年使用:0次
7 . 已知双曲线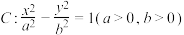 的右焦点为
的右焦点为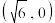 ,渐近线方程为
,渐近线方程为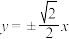 .
.
(1)求C的方程;
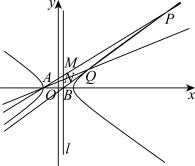
(2)记C的左顶点为A,直线
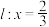 与x轴交于点B,过B的直线与C的右支于P,Q两点,直线AP,AQ分别交直线l于点M,N,证明O,A,M,N四点共圆.
与x轴交于点B,过B的直线与C的右支于P,Q两点,直线AP,AQ分别交直线l于点M,N,证明O,A,M,N四点共圆.
您最近半年使用:0次
解题方法
8 . 设点 是曲线
是曲线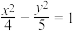 右支上一动点,
右支上一动点, 为左焦点,点
为左焦点,点 是圆
是圆 上一动点,则
上一动点,则 的最小值是
的最小值是
您最近半年使用:0次
23-24高二上·上海·课后作业
解题方法
9 . 数学家华罗庚曾说:“数缺形时少直观,形少数时难入微.”事实上,很多代数问题可以转化为几何问题加以解决.例如,与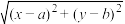 相关的代数问题,可以转化为点
相关的代数问题,可以转化为点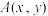 与点
与点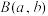 之间的距离的几何问题.结合上述观点,函数
之间的距离的几何问题.结合上述观点,函数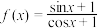 ,
,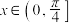 的值域为
的值域为______ .
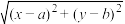 相关的代数问题,可以转化为点
相关的代数问题,可以转化为点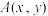 与点
与点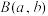 之间的距离的几何问题.结合上述观点,函数
之间的距离的几何问题.结合上述观点,函数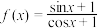 ,
,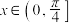 的值域为
的值域为
您最近半年使用:0次
10 . 已知点 在抛物线
在抛物线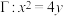 上运动,过点
上运动,过点 的两直线
的两直线 与圆
与圆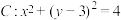 相切,切点分别为
相切,切点分别为 ,当
,当 取最小值时,直线
取最小值时,直线 的方程为
的方程为__________ .
 在抛物线
在抛物线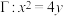 上运动,过点
上运动,过点 的两直线
的两直线 与圆
与圆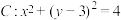 相切,切点分别为
相切,切点分别为 ,当
,当 取最小值时,直线
取最小值时,直线 的方程为
的方程为
您最近半年使用:0次



