解题方法
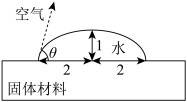
1 . 新材料是现代高新技术的基础和先导,亦是提升传统产业技术能级的关键.某科研小组研发的新材料水滴角测试结果如图所示(水滴角可看作液、固、气三相交点处气—液两相界面的切线与液—固两相交线所成的角),圆法和椭圆法是测量水滴角的常用方法,即将水滴轴截面看成圆或者椭圆(长轴平行于液—固两相交线)的一部分.设圆法和椭圆法测量所得水滴角分别为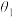 ,
,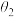 ,则( )
,则( )
附:椭圆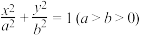 上一点
上一点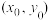 处的切线方程为
处的切线方程为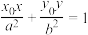 .
.
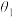 ,
,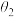 ,则( )
,则( )
附:椭圆
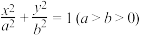 上一点
上一点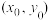 处的切线方程为
处的切线方程为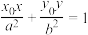 .
.A. | B. |
C.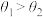 | D.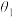 和 和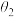 的大小关系无法确定 的大小关系无法确定 |
您最近半年使用:0次
名校
解题方法
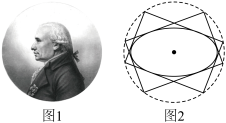
2 . 加斯帕尔·蒙日(图1)是18~19世纪法国著名的几何学家,他在研究圆锥曲线时发现:椭圆的任意两条互相垂直的切线的交点都在同一个圆上,其圆心是椭圆的中心,这个圆被称为“蒙日圆”(图2).则椭圆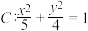 的蒙日圆的半径为
的蒙日圆的半径为___________
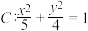 的蒙日圆的半径为
的蒙日圆的半径为
您最近半年使用:0次
解题方法
3 . 若曲线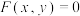 上的两点
上的两点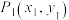 ,
,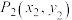 满足
满足 ,则称这两点为曲线
,则称这两点为曲线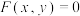 上的一对“双胞点”.下列曲线中:①
上的一对“双胞点”.下列曲线中:①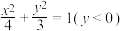 ;②
;②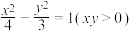 ;③
;③ ;④
;④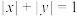 .存在“双胞点”的曲线序号是
.存在“双胞点”的曲线序号是_________ .
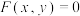 上的两点
上的两点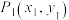 ,
,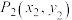 满足
满足 ,则称这两点为曲线
,则称这两点为曲线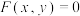 上的一对“双胞点”.下列曲线中:①
上的一对“双胞点”.下列曲线中:①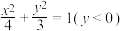 ;②
;②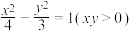 ;③
;③ ;④
;④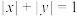 .存在“双胞点”的曲线序号是
.存在“双胞点”的曲线序号是
您最近半年使用:0次
4 . 曲线 是平面内与三个定点
是平面内与三个定点 ,
,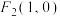 和
和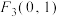 的距离的和等于
的距离的和等于 的点的轨迹.给出下列四个结论:
的点的轨迹.给出下列四个结论:
①曲线 关于
关于 轴、
轴、 轴均对称;
轴均对称;
②曲线 上存在点
上存在点 ,使得
,使得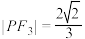 ;
;
③若点 在曲线
在曲线 上,则
上,则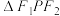 的面积最大值是1;
的面积最大值是1;
④曲线 上存在点
上存在点 ,使得
,使得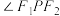 为钝角.
为钝角.
其中所有正确结论的序号是( )
 是平面内与三个定点
是平面内与三个定点 ,
,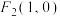 和
和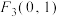 的距离的和等于
的距离的和等于 的点的轨迹.给出下列四个结论:
的点的轨迹.给出下列四个结论:①曲线
 关于
关于 轴、
轴、 轴均对称;
轴均对称;②曲线
 上存在点
上存在点 ,使得
,使得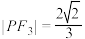 ;
;③若点
 在曲线
在曲线 上,则
上,则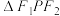 的面积最大值是1;
的面积最大值是1;④曲线
 上存在点
上存在点 ,使得
,使得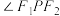 为钝角.
为钝角.其中所有正确结论的序号是( )
| A.②③④ | B.②③ | C.③④ | D.①②③④ |
您最近半年使用:0次
2024-01-25更新
|
278次组卷
|
3卷引用:四川省成都市石室中学2024届高三上学期期末数学(理)试题
名校
解题方法
5 . 下列说法中正确的是( )
| A.若直线的倾斜角越大,则直线的斜率就越大 |
B.若直线的倾斜角为 ,则直线的斜率为 ,则直线的斜率为 |
C.若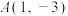 , , ,则直线 ,则直线 的倾斜角为 的倾斜角为 |
D.若直线过点 ,且它的倾斜角为 ,且它的倾斜角为 ,则这条直线必过点 ,则这条直线必过点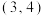 |
您最近半年使用:0次
19-20高二·全国·课后作业
解题方法
6 . 已知圆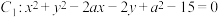 ,圆
,圆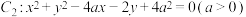 .试求
.试求 为何值时,两圆
为何值时,两圆 :
:
(1)相切;
(2)相交;
(3)外离;
(4)内含.
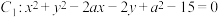 ,圆
,圆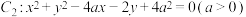 .试求
.试求 为何值时,两圆
为何值时,两圆 :
:(1)相切;
(2)相交;
(3)外离;
(4)内含.
您最近半年使用:0次
2023-10-06更新
|
587次组卷
|
9卷引用:【新教材精创】2.5.2+圆与圆的位置关系+导学案-人教A版高中数学选择性必修第一册
(已下线)【新教材精创】2.5.2+圆与圆的位置关系+导学案-人教A版高中数学选择性必修第一册北师大版(2019) 选修第一册 数学奇书 第一章 直线与圆 §2 圆与圆的方程 2.4 圆与圆的位置关系(已下线)复习题二湘教版(2019)选择性必修第一册课本习题第2章复习题(已下线)模块一 专题2 直线与圆的方程(2)(人教A)(已下线)专题10直线与圆、圆与圆的位置关系(4个知识点8种题型)-【倍速学习法】2023-2024学年高二数学核心知识点与常见题型通关讲解练(人教A版2019选修第一册)(已下线)第二章+直线与圆的方程(知识清单)(18个考点梳理+典型例题+变式训练)(已下线)2.5.2 圆与圆的位置关系【第一课】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)专题18 圆与圆的位置关系5种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)
7 . 已知点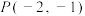 到直线l:
到直线l: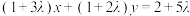 的距离为d,则d的可能取值是( )
的距离为d,则d的可能取值是( )
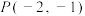 到直线l:
到直线l: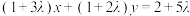 的距离为d,则d的可能取值是( )
的距离为d,则d的可能取值是( )| A.0 | B.1 | C. | D.4 |
您最近半年使用:0次
名校
解题方法
8 . 在平面直角坐标系中,已知 分别是椭圆
分别是椭圆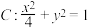 的左焦点和右焦点.
的左焦点和右焦点.
(1)设 是椭圆
是椭圆 上的任意一点,求
上的任意一点,求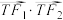 取值范围;
取值范围;
(2)设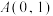 ,直线
,直线 与椭圆
与椭圆 交于
交于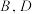 两点,若
两点,若 是以
是以 为直角顶点的等腰直角三角形,求直线
为直角顶点的等腰直角三角形,求直线 的方程.
的方程.
 分别是椭圆
分别是椭圆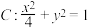 的左焦点和右焦点.
的左焦点和右焦点.(1)设
 是椭圆
是椭圆 上的任意一点,求
上的任意一点,求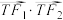 取值范围;
取值范围;(2)设
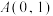 ,直线
,直线 与椭圆
与椭圆 交于
交于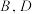 两点,若
两点,若 是以
是以 为直角顶点的等腰直角三角形,求直线
为直角顶点的等腰直角三角形,求直线 的方程.
的方程.
您最近半年使用:0次
2023-06-01更新
|
570次组卷
|
7卷引用:江苏省南京市2020-2021学年高三上学期9月期初数学试题
9 . 如图所示,在 的长方形区域(含边界)中有
的长方形区域(含边界)中有 两点,对于该区域中的点
两点,对于该区域中的点 ,若其到
,若其到 的距离不超过到
的距离不超过到 距离的一半,则称
距离的一半,则称 处于
处于 的控制下,例如原点
的控制下,例如原点 满足
满足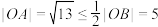 ,即有
,即有 点处于
点处于 的控制下.同理可定义
的控制下.同理可定义 处于
处于 的控制下.
的控制下.
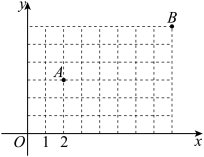
给出下列四个结论:
①点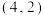 处于
处于 的控制下;
的控制下;
②若点 不处于
不处于 的控制下,则其必处于
的控制下,则其必处于 的控制下;
的控制下;
③若 处于
处于 的控制下,则
的控制下,则 ;
;
④图中所有处于 的控制下的点构成的区域面积为
的控制下的点构成的区域面积为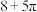 .
.
其中所有正确结论的序号是_________ .
 的长方形区域(含边界)中有
的长方形区域(含边界)中有 两点,对于该区域中的点
两点,对于该区域中的点 ,若其到
,若其到 的距离不超过到
的距离不超过到 距离的一半,则称
距离的一半,则称 处于
处于 的控制下,例如原点
的控制下,例如原点 满足
满足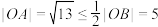 ,即有
,即有 点处于
点处于 的控制下.同理可定义
的控制下.同理可定义 处于
处于 的控制下.
的控制下.
给出下列四个结论:
①点
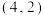 处于
处于 的控制下;
的控制下;②若点
 不处于
不处于 的控制下,则其必处于
的控制下,则其必处于 的控制下;
的控制下;③若
 处于
处于 的控制下,则
的控制下,则 ;
;④图中所有处于
 的控制下的点构成的区域面积为
的控制下的点构成的区域面积为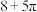 .
.其中所有正确结论的序号是
您最近半年使用:0次
2023-05-30更新
|
888次组卷
|
8卷引用:北京市师大附属中学2023届高三适应性练习数学试题
北京市师大附属中学2023届高三适应性练习数学试题北京市海淀区北京大学附属中学2023届高三三模数学试题(已下线)高二上学期第一次月考填空题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)高二上学期期中考试填空题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)四川省宜宾市叙州区叙州区第一中学校2023-2024学年高二上学期10月月考数学试题重庆市广益中学校2023-2024学年高二上学期10月月考数学试题(已下线)2.3.2 圆的一般方程(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第一册)(已下线)专题02 直线和圆的方程(5)
名校
解题方法
10 . 已知平面直角坐标系中的点集 ,给出下列四个结论:
,给出下列四个结论:
(1)当直线 为
为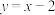 时,
时, 与
与 没有公共点;
没有公共点;
(2)存在直线 与
与 有且只有一个公共点;
有且只有一个公共点;
(3)存在直线 经过
经过 中的无穷个点;
中的无穷个点;
(4)存在直线 与
与 没有公共点,且
没有公共点,且 中存在两点在
中存在两点在 的两侧.
的两侧.
其中所有正确结论的序号是__________ .
 ,给出下列四个结论:
,给出下列四个结论:(1)当直线
 为
为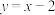 时,
时, 与
与 没有公共点;
没有公共点;(2)存在直线
 与
与 有且只有一个公共点;
有且只有一个公共点;(3)存在直线
 经过
经过 中的无穷个点;
中的无穷个点;(4)存在直线
 与
与 没有公共点,且
没有公共点,且 中存在两点在
中存在两点在 的两侧.
的两侧.其中所有正确结论的序号是
您最近半年使用:0次
2023-05-23更新
|
669次组卷
|
4卷引用:北京市海淀区2023届高三数学查缺补漏题(1)
北京市海淀区2023届高三数学查缺补漏题(1)北京市中关村中学2023届高三三模数学练习试题北京市第一零一中学2023届高三三模数学统考四试题(已下线)2.1.3 直线与圆的位置关系(八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)



