解题方法
1 . 有5把钥匙,其中有2把能打开锁,现从中任取1把能打开锁的概率是( )
A. | B. | C. | D. |
您最近半年使用:0次
名校
解题方法
2 . 有一个人在打靶中,连续射击2次,事件“至少有1次中靶”的对立事件是( ).
| A.至多有1次中靶 | B.2次都中靶 |
| C.2次都不中靶 | D.只有1次中靶 |
您最近半年使用:0次
2023-04-17更新
|
1640次组卷
|
26卷引用:沪教版(2020) 必修第三册 精准辅导 第12章 单元测试
沪教版(2020) 必修第三册 精准辅导 第12章 单元测试沪教版(2020) 必修第三册 新课改一课一练 第12章 12.2.3 事件关系与运算广东省深圳市龙岗区龙城高级中学2021-2022学年高二下学期期中数学试题湖南省邵阳市新邵县2017-2018学年高一下学期期末数学试题第12章 概率初步(单元提升卷)-2022-2023学年高二数学考试满分全攻略(沪教版2020必修第三册)陕西师范大学附属中学2022-2023学年高二上学期10月月考数学试题广西壮族自治区田阳高中2016-2017学年高二10月月考数学试题(文)广西壮族自治区田阳高中2016-2017学年高二10月月考数学试题(理)河北省高碑店市崇德实验中学2022-2023学年高二上学期期末数学试题第七章 概率 单元综合测试卷-2021-2022学年高一上学期数学北师大版(2019)必修第一册广东省珠海市斗门区第一中学2022-2023学年高二上学期期末数学试题(已下线)10.1 随机事件与概率(分层练习)(已下线)第十章概率(知识通关)(1)【单元测试卷】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第二册)第十章 概率(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第二册(已下线)10.1.1&10.1.2 有限样本空间与随机事件、事件的关系和运算(精练)-【题型分类归纳】(已下线)模块二 专题7 概率 B提升卷 (苏教版)山东省淄博实验中学2022-2023学年高二上学期期末数学试题云南省曲靖二中兴教中学2022-2023学年高二下学期第四次教学质量检测(6月)数学试题新疆乌鲁木齐市第101中学2023-2024学年高二上学期开学考试数学试题湖南省长沙市雅礼中学2023-2024学年高二下学期入学检测数学试题2023年湖南省衡阳市普通高中学业水平合格性仿真(F)数学试题湖北省武汉外国语学校2023-2024学年高二上学期9月月考数学试题广东省佛山市南海区南海中学分校2023-2024学年高二上学期10月阶段性测试数学试题海南省白沙黎族自治县白沙中学2021-2022学年高二上学期期末考试数学试题(已下线)1.4随机事件的运算-数学同步精品课堂(北师大版2019必修第一册)(已下线)艺体生一轮复习 第九章 计数原理、概率与统计 第44讲 随机事件的概率与古典概型【练】
3 . 某电视台的夏日水上闯关节目一共有三关,每一关都有两次闯关机会,第一关中每一次的过关率为 ,第二关中每一次的过关率为
,第二关中每一次的过关率为 ,只有通过前一关才能进入下一关,且通过每关相互独立.一名选手参加该节目,则该选手能进入第三关的概率为( )
,只有通过前一关才能进入下一关,且通过每关相互独立.一名选手参加该节目,则该选手能进入第三关的概率为( )
 ,第二关中每一次的过关率为
,第二关中每一次的过关率为 ,只有通过前一关才能进入下一关,且通过每关相互独立.一名选手参加该节目,则该选手能进入第三关的概率为( )
,只有通过前一关才能进入下一关,且通过每关相互独立.一名选手参加该节目,则该选手能进入第三关的概率为( )A. | B. | C.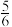 | D. |
您最近半年使用:0次
2021-09-24更新
|
168次组卷
|
4卷引用:陕西省西安市高新一中、交大附中、师大附中2019-2020学年高三上学期1月联考数学(文)试题
解题方法
4 . 对于概率是1‰(千分之一)的事件,下列说法正确的是( )
| A.概率太小,不可能发生 |
| B.1000次中一定发生1次 |
| C.1000人中,999人说不发生,1人说发生 |
| D.1000次中有可能发生1000次 |
您最近半年使用:0次
5 . 冬奥会的全称是冬季奥林匹克运动会,是世界规模最大的冬季综合性运动会,每四年举办一届.第24届冬奥会将于2022年在中国北京和张家口举行,为了弘扬奥林匹克精神,增强学生的冬奥会知识,某市多所中小学校开展了模拟冬奥会各项比赛的活动.为了了解学生在越野滑轮和旱地冰壶两项中的参与情况,在全市中小学学校中随机抽取了10所学校,10所学校的参与人数如下:
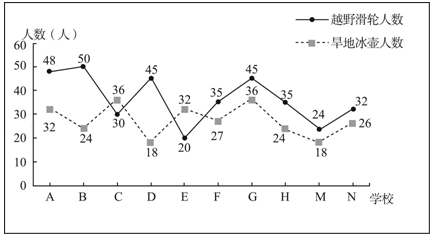
(1)现从这10所学校中随机选取2所学校进行调查,求选出的2所学校参与旱地冰壶人数在30人以下的概率.
(2)某校聘请了一名越野滑轮教练,对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导.规定:这3个动作中至少有2个动作达到“优”,总考核记为“优”.在指导前,该校甲同学3个动作中每个动作达到“优”的概率为0.1.在指导后的考核中,甲同学总考核成绩为“优”.能否认为甲同学在指导后总考核达到“优”的概率发生了变化?请说明理由.

(1)现从这10所学校中随机选取2所学校进行调查,求选出的2所学校参与旱地冰壶人数在30人以下的概率.
(2)某校聘请了一名越野滑轮教练,对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导.规定:这3个动作中至少有2个动作达到“优”,总考核记为“优”.在指导前,该校甲同学3个动作中每个动作达到“优”的概率为0.1.在指导后的考核中,甲同学总考核成绩为“优”.能否认为甲同学在指导后总考核达到“优”的概率发生了变化?请说明理由.
您最近半年使用:0次
2021-09-08更新
|
521次组卷
|
2卷引用:江苏省百校联考2021-2022学年高三上学期第一次考试数学试题
解题方法
6 . 从1,2,3,4,5,6这六个整数中任取两个数,下列各组事件中是对立事件的是( )
①恰有一个是偶数和恰有一个是奇数;②两个都是偶数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.
①恰有一个是偶数和恰有一个是奇数;②两个都是偶数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.
| A.① | B.②④ | C.③ | D.①③ |
您最近半年使用:0次
名校
解题方法
7 . 在刚刚过去的寒假,由于新冠疫情的影响,哈尔滨市的 、
、 两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取
两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取 名学生,对每名学生进行综合测试评分,记综合评分为
名学生,对每名学生进行综合测试评分,记综合评分为 及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有
及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有 名优秀学生,且
名优秀学生,且 学校的优秀学生占该校抽取总人数的
学校的优秀学生占该校抽取总人数的 .
.
(1)填写下面的列联表,并判断能否在犯错误概率不超过 的前提下认为学生综合测试评分优秀与教学方案有关.
的前提下认为学生综合测试评分优秀与教学方案有关.
(2)在 学校的
学校的 名学生中依据综合测评是否优秀进行分层抽样,抽取容量为
名学生中依据综合测评是否优秀进行分层抽样,抽取容量为 的样本,在
的样本,在 名学生中随机抽取
名学生中随机抽取 名同学,求
名同学,求 名同学都是优秀学生的概率.
名同学都是优秀学生的概率.
附:
 ,其中
,其中 .
.
 、
、 两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取
两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取 名学生,对每名学生进行综合测试评分,记综合评分为
名学生,对每名学生进行综合测试评分,记综合评分为 及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有
及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有 名优秀学生,且
名优秀学生,且 学校的优秀学生占该校抽取总人数的
学校的优秀学生占该校抽取总人数的 .
.(1)填写下面的列联表,并判断能否在犯错误概率不超过
 的前提下认为学生综合测试评分优秀与教学方案有关.
的前提下认为学生综合测试评分优秀与教学方案有关.(2)在
 学校的
学校的 名学生中依据综合测评是否优秀进行分层抽样,抽取容量为
名学生中依据综合测评是否优秀进行分层抽样,抽取容量为 的样本,在
的样本,在 名学生中随机抽取
名学生中随机抽取 名同学,求
名同学,求 名同学都是优秀学生的概率.
名同学都是优秀学生的概率.| 优秀学生 | 非优秀学生 | 合计 | |
| 甲方案 | |||
| 乙方案 | |||
| 合计 |
 | 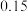 |  |  |  |  |  |  |
 | 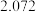 |  |  |  |  |  |  |
 ,其中
,其中 .
.
您最近半年使用:0次
2021-05-05更新
|
665次组卷
|
4卷引用:黑龙江省哈尔滨市第三中学2021届高三第三次模拟考试数学(文科)试题
黑龙江省哈尔滨市第三中学2021届高三第三次模拟考试数学(文科)试题(已下线)文科数学-2021年高考考前20天终极冲刺攻略+(三)(6月1日)全国Ⅱ卷决胜高考2021届高三数学(理)仿真卷试题(七)黑龙江省哈尔滨市第三中学校2021届高三三模数学(文)试题
19-20高三下·全国·阶段练习
解题方法
8 . 在机械化生产车间里,工人们在排列整齐的工作台旁紧张地生产同一种产品,工作台上方一条传送带在运转,带上设置若干钩子,钩子均匀排列,如图,工人将产品挂在经过他上方的钩子上带走.当生产进入稳定状态后,每个工人生产一件产品所需时间是不变的,而他挂产品的时刻是随机的.每个工人在任何时刻都能触到一只钩子,且只能触到一只,在他生产出一件产品的瞬间,如果他能触到的钩子是空的,则可将产品挂上带走;如果非空,则他只能将产品放下.放下的产品就永远退出这个传送系统.衡量这种传送系统的效率可以看它能否及时把工人的产品带走.显然,在工人数目不变的情况下传送带速度越快,带上钩子数越多,效率越高.设在一个周期内有m个钩子通过每一工作台上方,且到达第一个工作台上方的钩子都是空的.可将传送系统的效率D 定义为一个周期内(每个工人只生产一件产品)带走的产品数s与生产的全部产品数n之比,且满足关系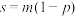 ,p为一个周期内每只钩子为空钩的概率.
,p为一个周期内每只钩子为空钩的概率.
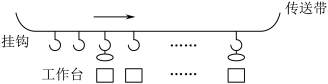
(1)当m=3,n=4时,求D的值;
(2)若m远大于n,试研究提高传送带效率的途径.
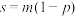 ,p为一个周期内每只钩子为空钩的概率.
,p为一个周期内每只钩子为空钩的概率.
(1)当m=3,n=4时,求D的值;
(2)若m远大于n,试研究提高传送带效率的途径.
您最近半年使用:0次
名校
解题方法
9 . 体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球;否则一直发到3次为止.设学生一次发球成功的概率为p(p≠0),发球次数为X,若X的数学期望E(X)>1.75,则p的取值可能是( )
A. | B. | C.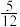 | D. |
您最近半年使用:0次
2020-10-31更新
|
1166次组卷
|
11卷引用:江苏省南京市秦淮中学2020-2021学年高三上学期10月月考数学试题
江苏省南京市秦淮中学2020-2021学年高三上学期10月月考数学试题(已下线)专题11.8 《计数原理、概率、随机变量及其分布列》单元测试卷-2021年新高考数学一轮复习学与练(已下线)4.2.4随机变量的数字特征(1)B提高练(已下线)专题4.6《随机变量》单元测试卷(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)(已下线)【新教材精创】7.3.1离散型随机变量的均值 -B提高练湖北省武汉市部分重点中学2020-2021学年高二下学期期中联考数学试题(已下线)第四章 概率与统计 4.2 随机变量 4.2.4 随机变量的数字特征江苏省苏州市常熟市2021-2022学年高二下学期期中数学试题山东学情2022-2023学年高二下学期3月联合考试数学试题B广东省东莞实验中学2022-2023学年高二下学期期中数学试题7.3.1离散型随机变量的均值练习
名校
解题方法
10 . 2019年10月20日,第六届世界互联网大会发布了15项“世界互联网领先科技成果”,其中有5项成果均属于芯片领域.现有3名学生从这15项“世界互联网领先科技成果”中分别任选1项进行了解,且学生之间的选择互不影响,则恰好有1名学生选择“芯片领域”的概率为( )
A.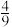 | B. | C.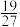 | D.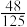 |
您最近半年使用:0次
2020-10-18更新
|
1796次组卷
|
15卷引用:湖南省益阳市2020-2021学年高三上学期9月调研考试数学试题
湖南省益阳市2020-2021学年高三上学期9月调研考试数学试题(已下线)痛点16 概率与统计中的综合问题-2021年新高考数学一轮复习考点扫描福建省莆田第二十五中学2021届高三上学期期中考试数学试题(已下线)4.2.3 二项分布与超几何分布-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第二册)(已下线)专题18 随机变量及其分布(客观题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)(已下线)专题19 随机变量及其分布(客观题)-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题27 概率与统计相结合问题(测)-2021年高三数学二轮复习讲练测(文理通用)(已下线)专题4.6《随机变量》单元测试卷(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)(已下线)专题15 随机变量的分布列与期望 -备战2021年新高考数学纠错笔记 (已下线)考点41 二项分布与正态分布-备战2022年高考数学(理)一轮复习考点微专题(已下线)7.4.1二项分布(作业)-【上好课】2020-2021学年高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)“8+4+4”小题强化训练(64)二项分布与正态分布-2022届高考数学一轮复习(江苏等新高考地区专用)人教B版(2019) 选修第二册 过关检测 第四章 4.2.3 二项分布与超几何分布(已下线)第13讲 离散型随机变量及其分布列-【寒假自学课】2022年高二数学寒假精品课(苏教版2019选择性必修第二册)(已下线)第七章 随机变量及其分布(能力提升)B卷-2021-2022学年高二数学课后培优练(人教A版2019选择性必修第三册)



