2024高三下·全国·专题练习
1 . 在 中,
中,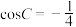 ,再从条件①、条件②、条件③中选择一个作为已知,使三角形唯一确定,求:
,再从条件①、条件②、条件③中选择一个作为已知,使三角形唯一确定,求:
(1) 的值;
的值;
(2) 的面积.
的面积.
条件①: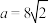 ,
,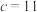 ;条件②:
;条件②: ,
,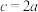 ;条件③:
;条件③: ,
, 为等腰三角形.
为等腰三角形.
 中,
中,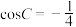 ,再从条件①、条件②、条件③中选择一个作为已知,使三角形唯一确定,求:
,再从条件①、条件②、条件③中选择一个作为已知,使三角形唯一确定,求:(1)
 的值;
的值;(2)
 的面积.
的面积.条件①:
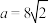 ,
,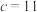 ;条件②:
;条件②: ,
,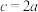 ;条件③:
;条件③: ,
, 为等腰三角形.
为等腰三角形.
您最近半年使用:0次
解题方法
2 . 如图,在五面体 中,底面
中,底面 为正方形,
为正方形,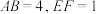 .
.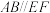 ;
;
(2)若 为
为 的中点,
的中点, 为
为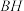 的中点,
的中点,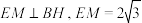 ,再从条件①、条件②这两个条件中选择一个作为已知,求直线
,再从条件①、条件②这两个条件中选择一个作为已知,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
条件①: ;
;
条件②: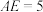 .
.
注:如果选择条件①和条件②分别解答,按第一个解答计分
 中,底面
中,底面 为正方形,
为正方形,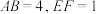 .
.
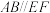 ;
;(2)若
 为
为 的中点,
的中点, 为
为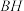 的中点,
的中点,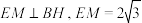 ,再从条件①、条件②这两个条件中选择一个作为已知,求直线
,再从条件①、条件②这两个条件中选择一个作为已知,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.条件①:
 ;
;条件②:
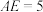 .
.注:如果选择条件①和条件②分别解答,按第一个解答计分
您最近半年使用:0次
名校
解题方法
3 . 如图,在四棱锥 中,底面ABCD是边长为2的正方形,
中,底面ABCD是边长为2的正方形, ,
, ,E为BC的中点,F为PD的中点.
,E为BC的中点,F为PD的中点.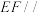 平面PAB;
平面PAB;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AD与平面AEF所成角的正弦值.
条件①: ;条件②:
;条件②: .
.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
 中,底面ABCD是边长为2的正方形,
中,底面ABCD是边长为2的正方形, ,
, ,E为BC的中点,F为PD的中点.
,E为BC的中点,F为PD的中点.
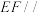 平面PAB;
平面PAB;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AD与平面AEF所成角的正弦值.
条件①:
 ;条件②:
;条件②: .
.注:如果选择条件①和条件②分别解答,按第一个解答计分.
您最近半年使用:0次
4 . 设正项数列 的前
的前 项和为
项和为 ,
, ,且满足_____.给出下列三个条件:
,且满足_____.给出下列三个条件:
① ,
, ; ②
; ② ;
;
③ .
.
请从其中任选一个将题目补充完整,并求解以下问题.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,
, ,且满足_____.给出下列三个条件:
,且满足_____.给出下列三个条件:①
 ,
, ; ②
; ② ;
;③
 .
.请从其中任选一个将题目补充完整,并求解以下问题.
(1)求数列
 的通项公式;
的通项公式;(2)若
 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近半年使用:0次
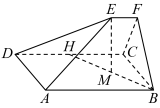
5 . 如图,边长为4的两个正三角形 ,
, 所在平面互相垂直,E,F分别为BC,CD的中点,点G在棱AD上,
所在平面互相垂直,E,F分别为BC,CD的中点,点G在棱AD上,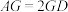 ,直线AB与平面
,直线AB与平面 相交于点H.
相交于点H.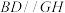 ;②直线HE,GF,AC相交于一点;
;②直线HE,GF,AC相交于一点;
注:若两个问题均作答,则按第一个计分.
(2)求直线BD与平面 的距离.
的距离.
 ,
, 所在平面互相垂直,E,F分别为BC,CD的中点,点G在棱AD上,
所在平面互相垂直,E,F分别为BC,CD的中点,点G在棱AD上,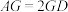 ,直线AB与平面
,直线AB与平面 相交于点H.
相交于点H.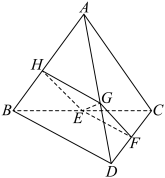
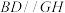 ;②直线HE,GF,AC相交于一点;
;②直线HE,GF,AC相交于一点;注:若两个问题均作答,则按第一个计分.
(2)求直线BD与平面
 的距离.
的距离.
您最近半年使用:0次
7日内更新
|
1475次组卷
|
3卷引用:江苏省南通市2024届高三第二次调研测试数学试题
6 . 在①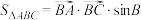 ,②
,②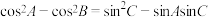 两个条件中任选一个补充在下列问题中,并解决该问题,
两个条件中任选一个补充在下列问题中,并解决该问题,
在 中,角A,B,C所对的边分别为a,b,c,_____,且
中,角A,B,C所对的边分别为a,b,c,_____,且 ,求:
,求:
(1)B;
(2) 周长的取值范围.
周长的取值范围.
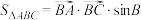 ,②
,②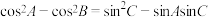 两个条件中任选一个补充在下列问题中,并解决该问题,
两个条件中任选一个补充在下列问题中,并解决该问题,在
 中,角A,B,C所对的边分别为a,b,c,_____,且
中,角A,B,C所对的边分别为a,b,c,_____,且 ,求:
,求:(1)B;
(2)
 周长的取值范围.
周长的取值范围.
您最近半年使用:0次
7 . 已知数列 ,______.在①数列
,______.在①数列 的前
的前 项和为
项和为 ,
,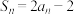 ;②数列
;②数列 的前
的前 项之积为
项之积为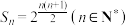 这两个条件中任选一个,补充在上面的问题中并解答(注:如果选择多个条件,按照第一个解答给分.在答题前应说明“我选______”)
这两个条件中任选一个,补充在上面的问题中并解答(注:如果选择多个条件,按照第一个解答给分.在答题前应说明“我选______”)
(1)求数列 的通项公式;
的通项公式;
(2)令 ,设数列
,设数列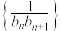 的前
的前 项和为
项和为 ,求证:
,求证: .
.
 ,______.在①数列
,______.在①数列 的前
的前 项和为
项和为 ,
,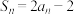 ;②数列
;②数列 的前
的前 项之积为
项之积为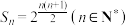 这两个条件中任选一个,补充在上面的问题中并解答(注:如果选择多个条件,按照第一个解答给分.在答题前应说明“我选______”)
这两个条件中任选一个,补充在上面的问题中并解答(注:如果选择多个条件,按照第一个解答给分.在答题前应说明“我选______”)(1)求数列
 的通项公式;
的通项公式;(2)令
 ,设数列
,设数列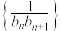 的前
的前 项和为
项和为 ,求证:
,求证: .
.
您最近半年使用:0次
8 . 记 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知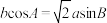 .
.
(1)求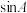 ;
;
(2)若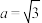 ,再从条件①,条件②,条件③中选择一个条件作为已知,使其能够确定唯一的三角形,并求
,再从条件①,条件②,条件③中选择一个条件作为已知,使其能够确定唯一的三角形,并求 的面积.
的面积.
条件① : ;条件② :
;条件② :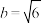 ;条件③ :
;条件③ : .
.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知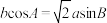 .
.(1)求
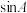 ;
;(2)若
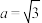 ,再从条件①,条件②,条件③中选择一个条件作为已知,使其能够确定唯一的三角形,并求
,再从条件①,条件②,条件③中选择一个条件作为已知,使其能够确定唯一的三角形,并求 的面积.
的面积.条件① :
 ;条件② :
;条件② :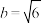 ;条件③ :
;条件③ : .
.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
您最近半年使用:0次
解题方法
9 . 已知定点 ,动点
,动点 在直线
在直线 上,过点
上,过点 作
作 的垂线,该垂线与
的垂线,该垂线与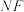 的垂直平分线交于点
的垂直平分线交于点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求 的方程;
的方程;
(2)已知点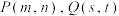 ,动点
,动点 在
在 上,满足
上,满足 ,且
,且 与
与 轴不垂直.请从①
轴不垂直.请从① 在
在 上;②
上;②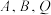 三点共线;③
三点共线;③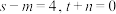 中选取两个作为条件,证明另外一个成立.
中选取两个作为条件,证明另外一个成立.
注:如果选择不同的组合分别解答,按第一个解答计分.
 ,动点
,动点 在直线
在直线 上,过点
上,过点 作
作 的垂线,该垂线与
的垂线,该垂线与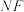 的垂直平分线交于点
的垂直平分线交于点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.(1)求
 的方程;
的方程;(2)已知点
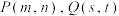 ,动点
,动点 在
在 上,满足
上,满足 ,且
,且 与
与 轴不垂直.请从①
轴不垂直.请从① 在
在 上;②
上;②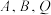 三点共线;③
三点共线;③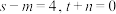 中选取两个作为条件,证明另外一个成立.
中选取两个作为条件,证明另外一个成立.注:如果选择不同的组合分别解答,按第一个解答计分.
您最近半年使用:0次
名校
解题方法
10 . 如图所示,将边长为2的正方形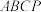 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,
, 为
为 的中点.
的中点.
(2)再从条件①、条件②这两个条件中选择一个作为已知,求二面角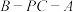 的余弦值及点
的余弦值及点 到平面
到平面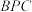 的距离.
的距离.
①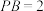 ;②
;②
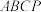 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,
, 为
为 的中点.
的中点.

(2)再从条件①、条件②这两个条件中选择一个作为已知,求二面角
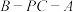 的余弦值及点
的余弦值及点 到平面
到平面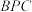 的距离.
的距离.①
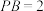 ;②
;②
您最近半年使用:0次



