名校
解题方法
1 . 下列函数中最小值为2的是( )
A. | B.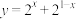 |
C.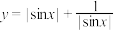 | D.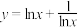 |
您最近半年使用:0次
名校
解题方法
2 . 已知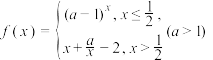 的值域为
的值域为 ,
,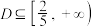 ,则
,则 的取值范围是( )
的取值范围是( )
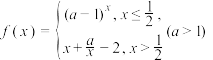 的值域为
的值域为 ,
,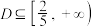 ,则
,则 的取值范围是( )
的取值范围是( )A. | B. | C.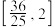 | D. |
您最近半年使用:0次
3 . 已知三角形ABC中,内角A,B,C所对边分别为a,b,c,且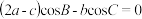 .
.
(1)求角B;
(2)若b=2,求 的取值范围.
的取值范围.
(3)若b=2,求三角形ABC面积的最大值.
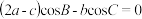 .
.(1)求角B;
(2)若b=2,求
 的取值范围.
的取值范围.(3)若b=2,求三角形ABC面积的最大值.
您最近半年使用:0次
名校
解题方法
4 . 下列结论正确的是
①当 时,
时,
②当 时,
时, 的最小值是2;
的最小值是2;
③设 ,
,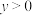 ,且
,且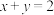 ,则
,则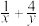 的最小值是
的最小值是 .
.
您最近半年使用:0次
解题方法
5 . 已知函数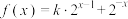 是偶函数,
是偶函数,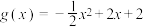 .
.
(1)求函数
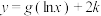 的零点;
的零点;(2)当
 时,函数
时,函数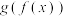 与
与 的值域相同,求
的值域相同,求 的最大值.
的最大值.
您最近半年使用:0次
名校
解题方法
6 . 求下列函数的值域:
(1)
(2)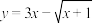
(3)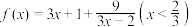
(1)

(2)
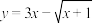
(3)
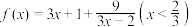
您最近半年使用:0次
解题方法
7 . 某快递公司为提高效率,引进智能机器人分拣系统,以提高分拣效率和降低物流成本.已知购买 台机器人的总成本为
台机器人的总成本为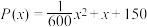 (单位:万元).若要使每台机器人的平均成本最低,则应买机器人
(单位:万元).若要使每台机器人的平均成本最低,则应买机器人___________ 台.
 台机器人的总成本为
台机器人的总成本为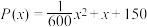 (单位:万元).若要使每台机器人的平均成本最低,则应买机器人
(单位:万元).若要使每台机器人的平均成本最低,则应买机器人
您最近半年使用:0次
名校
解题方法
8 . 已知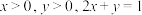 ,则( )
,则( )
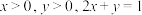 ,则( )
,则( )A. 的最小值为 的最小值为  | B. 的最大值为 的最大值为 |
C.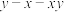 的最小值为 的最小值为  | D.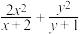 的最小值为 的最小值为 |
您最近半年使用:0次
2024-03-07更新
|
479次组卷
|
3卷引用:福建省泉州市2023-2024学年高一上学期1月期末教学质量监测数学试题
福建省泉州市2023-2024学年高一上学期1月期末教学质量监测数学试题(已下线)微考点1-1 新高考新试卷结构中不等式压轴4大考点总结江西省宜春市宜春中学2023-2024学年高一下学期开学考试数学试题
2024·全国·模拟预测
名校
解题方法
9 . 若实数a,b,c满足条件: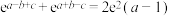 ,则
,则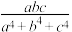 的最大值是
的最大值是______ .
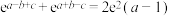 ,则
,则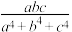 的最大值是
的最大值是
您最近半年使用:0次
2024-03-06更新
|
587次组卷
|
6卷引用:2024届数学新高考学科基地秘卷(七)
(已下线)2024届数学新高考学科基地秘卷(七)广东省广州市广东实验中学2024届高三上学期第二次阶段测试数学试题(已下线)经典好题1 积常和小 和常积大【练】(已下线)高考数学冲刺押题卷02(2024新题型)(已下线)黄金卷08(2024新题型)吉林省长春外国语学校2023-2024学年高二下学期4月月考数学试卷
解题方法
10 . 某药品可用于治疗某种疾病,经检测知每注射tml药品,从注射时间起血药浓度y(单位:ug/ml)与药品在体内时间 (单位:小时)的关系如下:
(单位:小时)的关系如下: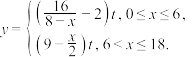 当血药浓度不低于
当血药浓度不低于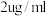 时才能起到有效治疗的作用,每次注射药品不超过
时才能起到有效治疗的作用,每次注射药品不超过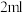 .
.
(1)若注射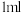 药品,求药品的有效治疗时间;
药品,求药品的有效治疗时间;
(2)若多次注射,则某一时刻体内血药浓度为每次注射后相应时刻血药浓度之和.已知病人第一次注射1ml药品,12小时之后又注射aml药品,要使随后的6小时内药品能够持续有效消疗,求 的最小值.
的最小值.
 (单位:小时)的关系如下:
(单位:小时)的关系如下: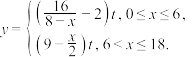 当血药浓度不低于
当血药浓度不低于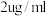 时才能起到有效治疗的作用,每次注射药品不超过
时才能起到有效治疗的作用,每次注射药品不超过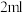 .
.(1)若注射
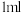 药品,求药品的有效治疗时间;
药品,求药品的有效治疗时间;(2)若多次注射,则某一时刻体内血药浓度为每次注射后相应时刻血药浓度之和.已知病人第一次注射1ml药品,12小时之后又注射aml药品,要使随后的6小时内药品能够持续有效消疗,求
 的最小值.
的最小值.
您最近半年使用:0次



