解题方法
1 . 若函数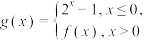 为奇函数,则函数
为奇函数,则函数 ,
, 的值域为
的值域为________ .
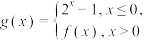 为奇函数,则函数
为奇函数,则函数 ,
, 的值域为
的值域为
您最近半年使用:0次
解题方法
2 . 早在西元前6世纪,毕达哥拉斯学派已经知道算术中项,几何中项以及调和中项,毕达哥拉斯学派哲学家阿契塔在《论音乐》中定义了上述三类中项,其中算术中项,几何中项的定义与今天大致相同.若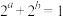 ,则
,则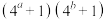 的最小值为( )
的最小值为( )
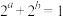 ,则
,则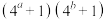 的最小值为( )
的最小值为( )A.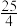 | B.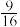 | C. | D.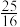 |
您最近半年使用:0次
名校
解题方法
3 . 在工程中估算平整一块矩形场地的工程量W(单位:平方米)的计算公式是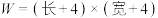 ,在不测量长和宽的情况下,若只知道这块矩形场地的面积是10000平方米,每平方米收费1元,请估算平整完这块场地所需的最少费用(单位:元)是( )
,在不测量长和宽的情况下,若只知道这块矩形场地的面积是10000平方米,每平方米收费1元,请估算平整完这块场地所需的最少费用(单位:元)是( )
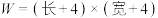 ,在不测量长和宽的情况下,若只知道这块矩形场地的面积是10000平方米,每平方米收费1元,请估算平整完这块场地所需的最少费用(单位:元)是( )
,在不测量长和宽的情况下,若只知道这块矩形场地的面积是10000平方米,每平方米收费1元,请估算平整完这块场地所需的最少费用(单位:元)是( )| A.10000 | B.10480 | C.10816 | D.10818 |
您最近半年使用:0次
今日更新
|
561次组卷
|
2卷引用:广东省韶关市2024届高三综合测试(二)数学试题
2024·全国·模拟预测
4 . 已知集合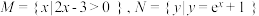 ,则( )
,则( )
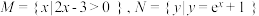 ,则( )
,则( )A. | B. | C. | D. |
您最近半年使用:0次
解题方法
5 . 设函数 ,若
,若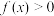 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
 ,若
,若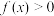 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )A. | B. |
C.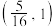 | D. |
您最近半年使用:0次
2024·全国·模拟预测
解题方法
6 . 已知 ,
, ,且
,且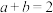 ,则( )
,则( )
 ,
, ,且
,且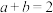 ,则( )
,则( )A.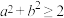 | B.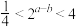 | C. | D.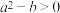 |
您最近半年使用:0次
解题方法
7 . 某乡镇为了打造“网红”城镇发展经济,因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现:某珍惜水果树的单株产量W(单位:千克)与施用肥料x(单位:千克)满足如下关系: ,肥料成本投入为10x元,其它成本投入(如培育管理、施肥等人工费)20x元.已知这种水果的市场售价大约15元/千克,且销售畅通供不应求,记该水果单株利润为
,肥料成本投入为10x元,其它成本投入(如培育管理、施肥等人工费)20x元.已知这种水果的市场售价大约15元/千克,且销售畅通供不应求,记该水果单株利润为 (单位:元)
(单位:元)
(1)写单株利润 (元)关于施用肥料x(千克)的关系式;
(元)关于施用肥料x(千克)的关系式;
(2)当施用肥料为多少千克时,该水果单株利润最大?最大利润是多少?
 ,肥料成本投入为10x元,其它成本投入(如培育管理、施肥等人工费)20x元.已知这种水果的市场售价大约15元/千克,且销售畅通供不应求,记该水果单株利润为
,肥料成本投入为10x元,其它成本投入(如培育管理、施肥等人工费)20x元.已知这种水果的市场售价大约15元/千克,且销售畅通供不应求,记该水果单株利润为 (单位:元)
(单位:元)(1)写单株利润
 (元)关于施用肥料x(千克)的关系式;
(元)关于施用肥料x(千克)的关系式;(2)当施用肥料为多少千克时,该水果单株利润最大?最大利润是多少?
您最近半年使用:0次
名校
解题方法
8 . 已知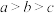 且
且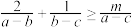 恒成立,实数
恒成立,实数 的最大值是
的最大值是_________ .
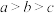 且
且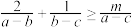 恒成立,实数
恒成立,实数 的最大值是
的最大值是
您最近半年使用:0次
名校
9 . 如图是函数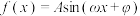 (
( ,
, ,
,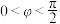 )的部分图像,M,N是它与x轴的两个不同交点,D是M,N之间的最高点且横坐标为
)的部分图像,M,N是它与x轴的两个不同交点,D是M,N之间的最高点且横坐标为 ,点
,点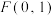 是线段DM的中点.
是线段DM的中点. 的解析式;
的解析式;
(2)若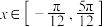 时,函数
时,函数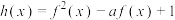 的最小值为
的最小值为 ,求实数a的值.
,求实数a的值.
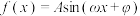 (
( ,
, ,
,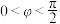 )的部分图像,M,N是它与x轴的两个不同交点,D是M,N之间的最高点且横坐标为
)的部分图像,M,N是它与x轴的两个不同交点,D是M,N之间的最高点且横坐标为 ,点
,点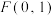 是线段DM的中点.
是线段DM的中点.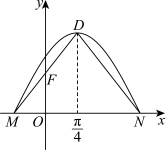
 的解析式;
的解析式;(2)若
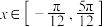 时,函数
时,函数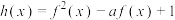 的最小值为
的最小值为 ,求实数a的值.
,求实数a的值.
您最近半年使用:0次
解题方法
10 . 已知函数 .
.
(1)判断并证明函数 在
在 上的单调性;
上的单调性;
(2)若存在 ,
,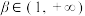 ,使得函数
,使得函数 在区间
在区间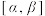 上的值域为
上的值域为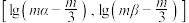 ,求实数
,求实数 的取值范围.
的取值范围.
 .
.(1)判断并证明函数
 在
在 上的单调性;
上的单调性;(2)若存在
 ,
,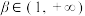 ,使得函数
,使得函数 在区间
在区间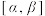 上的值域为
上的值域为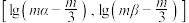 ,求实数
,求实数 的取值范围.
的取值范围.
您最近半年使用:0次



