1 . 已知函数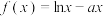 ,
,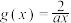 ,
, .
.
(1)求函数 的单调区间;
的单调区间;
(2)若 且
且 恒成立,求
恒成立,求 的最小值.
的最小值.
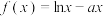 ,
,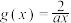 ,
, .
.(1)求函数
 的单调区间;
的单调区间;(2)若
 且
且 恒成立,求
恒成立,求 的最小值.
的最小值.
您最近半年使用:0次
2 . 已知函数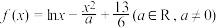 .
.
(1)讨论函数 的单调性;
的单调性;
(2)当 时,证明:对任意的
时,证明:对任意的 ,
, .
.
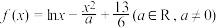 .
.(1)讨论函数
 的单调性;
的单调性;(2)当
 时,证明:对任意的
时,证明:对任意的 ,
, .
.
您最近半年使用:0次
3 . 已知 .
.
(1)讨论 的单调性;
的单调性;
(2)若 ,求
,求 的取值范围.
的取值范围.
 .
.(1)讨论
 的单调性;
的单调性;(2)若
 ,求
,求 的取值范围.
的取值范围.
您最近半年使用:0次
4 . 函数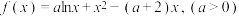 .
.
(1)函数 的单调性;
的单调性;
(2)数 在区间
在区间 上的最小值
上的最小值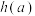 .
.
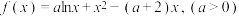 .
.(1)函数
 的单调性;
的单调性;(2)数
 在区间
在区间 上的最小值
上的最小值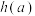 .
.
您最近半年使用:0次
5 . 已知函数 (
( ,
, ).
).
(1)讨论 的单调性;
的单调性;
(2)若 存在极值点
存在极值点 ,证明:
,证明: 随着
随着 的增大而增大.
的增大而增大.
 (
( ,
, ).
).(1)讨论
 的单调性;
的单调性;(2)若
 存在极值点
存在极值点 ,证明:
,证明: 随着
随着 的增大而增大.
的增大而增大.
您最近半年使用:0次
6 . 已知函数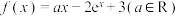 ,
,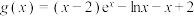 .
.
(1)求函数 的单调区间;
的单调区间;
(2)记函数 的导函数为
的导函数为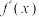 ,若不等式
,若不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
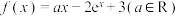 ,
,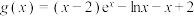 .
.(1)求函数
 的单调区间;
的单调区间;(2)记函数
 的导函数为
的导函数为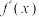 ,若不等式
,若不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
名校
7 . 函数 .
.
(1)若函数 在区间
在区间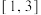 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)当 时,讨论函数
时,讨论函数 在区间
在区间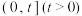 上的单调性.
上的单调性.
 .
.(1)若函数
 在区间
在区间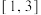 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;(2)当
 时,讨论函数
时,讨论函数 在区间
在区间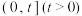 上的单调性.
上的单调性.
您最近半年使用:0次
昨日更新
|
1870次组卷
|
3卷引用:四川省遂宁市射洪中学2023-2024学年高二下学期第一次半月考数学试题
四川省遂宁市射洪中学2023-2024学年高二下学期第一次半月考数学试题广东省东莞市常平中学2023-2024学年高二下学期3月阶段检测数学试题(已下线)高二下学期期中考试(范围:数列、导数、计数原理)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
名校
8 . 已知函数 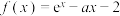 ,
, ,
, 是自然对数的底数.
是自然对数的底数.
(1)讨论函数 的单调性;
的单调性;
(2)若关于 的方程
的方程 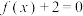 有两个不等实根,求
有两个不等实根,求 的取值范围;
的取值范围;
(3)若 ,
, 为整数,且当
为整数,且当 时,
时, 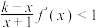 恒成立,求
恒成立,求  的最大值.
的最大值.
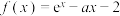 ,
, ,
, 是自然对数的底数.
是自然对数的底数.(1)讨论函数
 的单调性;
的单调性;(2)若关于
 的方程
的方程 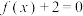 有两个不等实根,求
有两个不等实根,求 的取值范围;
的取值范围;(3)若
 ,
, 为整数,且当
为整数,且当 时,
时, 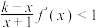 恒成立,求
恒成立,求  的最大值.
的最大值.
您最近半年使用:0次
名校
9 . 已知函数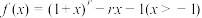 ,
, 且
且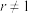 .
.
(1)讨论 的单调性;
的单调性;
(2)比较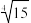 与
与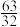 的大小,并说明理由;
的大小,并说明理由;
(3)当 时,证明:
时,证明: .
.
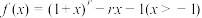 ,
, 且
且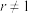 .
.(1)讨论
 的单调性;
的单调性;(2)比较
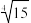 与
与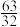 的大小,并说明理由;
的大小,并说明理由;(3)当
 时,证明:
时,证明: .
.
您最近半年使用:0次
昨日更新
|
190次组卷
|
2卷引用:河南省名校2023-2024学年高三下学期高考模拟4月联考数学试题
名校
10 . 已知函数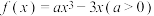 在区间
在区间 上的最小值为-2.
上的最小值为-2.
(1)求a;
(2)(ⅰ)若过点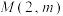 存在2条直线与曲线
存在2条直线与曲线 相切,求m的值;
相切,求m的值;
(ⅱ)问过点 ,
, ,
,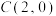 分别存在几条直线与曲线
分别存在几条直线与曲线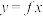 相切?(只需写出结论)
相切?(只需写出结论)
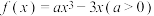 在区间
在区间 上的最小值为-2.
上的最小值为-2.(1)求a;
(2)(ⅰ)若过点
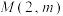 存在2条直线与曲线
存在2条直线与曲线 相切,求m的值;
相切,求m的值;(ⅱ)问过点
 ,
, ,
,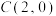 分别存在几条直线与曲线
分别存在几条直线与曲线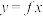 相切?(只需写出结论)
相切?(只需写出结论)
您最近半年使用:0次



