21-22高二·江苏·课后作业
1 . 椭圆经过点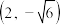 和
和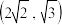 ,则该椭圆的标准方程为
,则该椭圆的标准方程为______ .
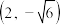 和
和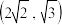 ,则该椭圆的标准方程为
,则该椭圆的标准方程为
您最近一年使用:0次
2022-03-01更新
|
677次组卷
|
3卷引用:本章测试3
21-22高二·江苏·课后作业
解题方法
2 . 求适合下列条件的椭圆的标准方程:
(1)中心在原点,焦点在x轴上,长轴长、短轴长分别为8和6;
(2)中心在原点,一个焦点坐标为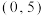 ,短轴长为4;
,短轴长为4;
(3)对称轴都在坐标轴上,长半轴长为10,离心率是0.6;
(4)中心在原点,焦点在x轴上,右焦点到短轴端点的距离为2,到右顶点的距离为1.
(1)中心在原点,焦点在x轴上,长轴长、短轴长分别为8和6;
(2)中心在原点,一个焦点坐标为
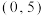 ,短轴长为4;
,短轴长为4;(3)对称轴都在坐标轴上,长半轴长为10,离心率是0.6;
(4)中心在原点,焦点在x轴上,右焦点到短轴端点的距离为2,到右顶点的距离为1.
您最近一年使用:0次
3 . 在推导椭圆的标准方程时,我们曾得到这样一个方程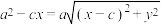 ,将其变形为
,将其变形为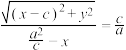 ,你能解释这个方程的几何意义吗?
,你能解释这个方程的几何意义吗?
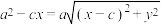 ,将其变形为
,将其变形为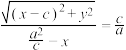 ,你能解释这个方程的几何意义吗?
,你能解释这个方程的几何意义吗?
您最近一年使用:0次
21-22高二·江苏·课后作业
解题方法
4 . 如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1处,片门位于另一个焦点F2处.从焦点F1处发出的光线,经过旋转椭圆面反射后集中到焦点F2处.已知BC⊥F1F2,F1B=3.2cm,F1F2=6cm.试建立适当的平面直角坐标系,求截口BAC所在椭圆的方程.
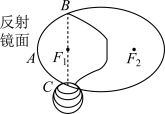
您最近一年使用:0次
21-22高二·江苏·课后作业
5 . 求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,长轴长为4,焦距为2;
(2)一个焦点坐标为 ,短轴长为2;
,短轴长为2;
(3)离心率为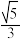 ,短轴长为4.
,短轴长为4.
(1)焦点在x轴上,长轴长为4,焦距为2;
(2)一个焦点坐标为
 ,短轴长为2;
,短轴长为2;(3)离心率为
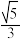 ,短轴长为4.
,短轴长为4.
您最近一年使用:0次
2022-02-28更新
|
1163次组卷
|
3卷引用:3.1.2 椭圆的几何性质
6 . 已知动点M(x,y)到定点F(3,0)的距离和点M到定直线l:x=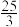 的距离之比是常数
的距离之比是常数 ,求动点M的轨迹.
,求动点M的轨迹.
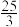 的距离之比是常数
的距离之比是常数 ,求动点M的轨迹.
,求动点M的轨迹.
您最近一年使用:0次
21-22高二·江苏·课后作业
7 . 求下列椭圆的焦点坐标:
(1)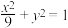
(2)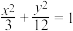 ;
;
(3)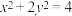 ;
;
(4)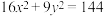 .
.
(1)
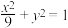
(2)
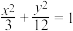 ;
;(3)
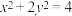 ;
;(4)
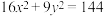 .
.
您最近一年使用:0次
21-22高二·江苏·课后作业
8 . 求焦点在坐标轴上,且经过点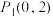 ,
,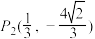 的椭圆的标准方程.
的椭圆的标准方程.
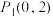 ,
,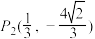 的椭圆的标准方程.
的椭圆的标准方程.
您最近一年使用:0次
21-22高二·江苏·课后作业
9 . 设m为实数,若方程 表示焦点在y轴上的椭圆,求m的取值范围.
表示焦点在y轴上的椭圆,求m的取值范围.
 表示焦点在y轴上的椭圆,求m的取值范围.
表示焦点在y轴上的椭圆,求m的取值范围.
您最近一年使用:0次
21-22高二·江苏·课后作业
10 . 求适合下列条件的椭圆的标准方程:
(1) ,
, ,焦点在x轴上;
,焦点在x轴上;
(2) ,
,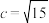 ,焦点在y轴上;
,焦点在y轴上;
(3)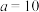 ,
, .
.
(1)
 ,
, ,焦点在x轴上;
,焦点在x轴上;(2)
 ,
,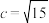 ,焦点在y轴上;
,焦点在y轴上;(3)
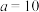 ,
, .
.
您最近一年使用:0次



