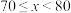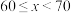解题方法
1 . 已知抛物线Γ: 的焦点为F,P为Γ上一动点.过F且斜率大于0的直线与Γ交于不同的两点A,B,且满足
的焦点为F,P为Γ上一动点.过F且斜率大于0的直线与Γ交于不同的两点A,B,且满足 ,
, .则下列说法错误的是( )
.则下列说法错误的是( )
 的焦点为F,P为Γ上一动点.过F且斜率大于0的直线与Γ交于不同的两点A,B,且满足
的焦点为F,P为Γ上一动点.过F且斜率大于0的直线与Γ交于不同的两点A,B,且满足 ,
, .则下列说法错误的是( )
.则下列说法错误的是( )| A.直线AB的倾斜角大于60° |
B.若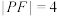 ,则 ,则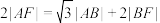 |
| C.点P可能在第一象限 |
D.直线PB的横截距不可能是 |
您最近一年使用:0次
2 . 已知抛物线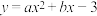 经过点
经过点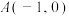 ,且与x轴右侧交于点B,对称轴为直线
,且与x轴右侧交于点B,对称轴为直线 ,与y轴交于点C.
,与y轴交于点C.
(2)如图1,过点 作直线
作直线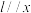 轴交抛物线于点
轴交抛物线于点 ,点
,点 在抛物线上,且
在抛物线上,且 ,求点
,求点 的坐标;
的坐标;
(3)如图2,直线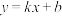 (
( )交抛物线于M,N两点,
)交抛物线于M,N两点, 轴于点H,
轴于点H,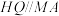 ,HQ与MN相交于点Q,求点Q的横坐标.
,HQ与MN相交于点Q,求点Q的横坐标.
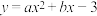 经过点
经过点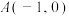 ,且与x轴右侧交于点B,对称轴为直线
,且与x轴右侧交于点B,对称轴为直线 ,与y轴交于点C.
,与y轴交于点C.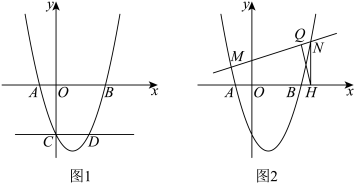
(2)如图1,过点
 作直线
作直线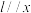 轴交抛物线于点
轴交抛物线于点 ,点
,点 在抛物线上,且
在抛物线上,且 ,求点
,求点 的坐标;
的坐标;(3)如图2,直线
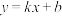 (
( )交抛物线于M,N两点,
)交抛物线于M,N两点, 轴于点H,
轴于点H,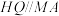 ,HQ与MN相交于点Q,求点Q的横坐标.
,HQ与MN相交于点Q,求点Q的横坐标.
您最近一年使用:0次
解题方法
3 . 为推动习近平新时代中国特色社会主义思想深入人心,促进全社会形成爱读书、读好书、善读书的新风尚,培育有坚定理想信念、爱党爱国、堪当民族复兴大任的有为青年,某学校举办了读书节活动.现从该校的2000名学生中发放调查问卷,随机调查了100名学生一周的课外阅读时间,将统计数据按照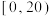 ,
,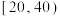 ,…
,…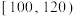 ,
,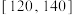 组后绘制成如图所示的频率分布直方图(单位:分钟,同一组中的数据用该组区间的中点值作代表).
组后绘制成如图所示的频率分布直方图(单位:分钟,同一组中的数据用该组区间的中点值作代表). 的值,若每周课外阅读时间60分钟以上(含60分钟)视为达标,试估计该校达标的人数;
的值,若每周课外阅读时间60分钟以上(含60分钟)视为达标,试估计该校达标的人数;
(2)估计该校学生每周课外阅读的平均时间;
(3)若样本数据在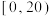 与
与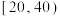 内的方差分别为
内的方差分别为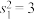 ,
,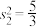 ,计样本数据在
,计样本数据在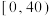 内的方差
内的方差 .
.
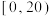 ,
,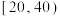 ,…
,…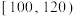 ,
,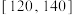 组后绘制成如图所示的频率分布直方图(单位:分钟,同一组中的数据用该组区间的中点值作代表).
组后绘制成如图所示的频率分布直方图(单位:分钟,同一组中的数据用该组区间的中点值作代表).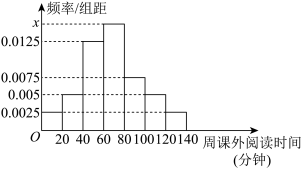
 的值,若每周课外阅读时间60分钟以上(含60分钟)视为达标,试估计该校达标的人数;
的值,若每周课外阅读时间60分钟以上(含60分钟)视为达标,试估计该校达标的人数;(2)估计该校学生每周课外阅读的平均时间;
(3)若样本数据在
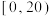 与
与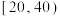 内的方差分别为
内的方差分别为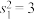 ,
,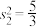 ,计样本数据在
,计样本数据在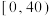 内的方差
内的方差 .
.
您最近一年使用:0次
解题方法
4 . 某企业进入中学参与学校举办的模拟招聘会,设置了笔试、面试两个环节,先笔试后面试,笔试通过了才可以进入面试,面试通过后即可录用,李明参加该企业的模拟招聘.
笔试关:有4道题,应聘者随机从中选择2道,两道题均答对即可通过笔试,否则淘汰不予录用.已知李明能答对其中的3道题;
面试关:有2道题,面试者答对第一道题,则面试通过被企业录用,否则就继续答第二道题,答对第二道题则面试通过被企业录用,否则淘汰不予录用.已知李明答对每道面试题的概率都是 ,两道题能否答对相互独立.
,两道题能否答对相互独立.
(1)李明笔试关中能答对的3道题记为 ,
, ,
, ,不能答对的题记为
,不能答对的题记为 ,请写出李明参加笔试关所有可能结果构成的样本空间,并求出李明通过笔试关的概率;
,请写出李明参加笔试关所有可能结果构成的样本空间,并求出李明通过笔试关的概率;
(2)求李明被录用的概率.
笔试关:有4道题,应聘者随机从中选择2道,两道题均答对即可通过笔试,否则淘汰不予录用.已知李明能答对其中的3道题;
面试关:有2道题,面试者答对第一道题,则面试通过被企业录用,否则就继续答第二道题,答对第二道题则面试通过被企业录用,否则淘汰不予录用.已知李明答对每道面试题的概率都是
 ,两道题能否答对相互独立.
,两道题能否答对相互独立.(1)李明笔试关中能答对的3道题记为
 ,
, ,
, ,不能答对的题记为
,不能答对的题记为 ,请写出李明参加笔试关所有可能结果构成的样本空间,并求出李明通过笔试关的概率;
,请写出李明参加笔试关所有可能结果构成的样本空间,并求出李明通过笔试关的概率;(2)求李明被录用的概率.
您最近一年使用:0次
5 . 某报刊对男女学生是否喜欢书法进行了一次随机调查,调查的数据如下表所示:
(1)根据表中的数据回答:是否喜欢书法与学生性别有关吗?
附: ,显著性水平取0.05,
,显著性水平取0.05, .
.
(2)现从上述96人中,按是否喜欢书法采用分层抽样的方法抽取12人进行问卷调查.若从这12人中任选4人,记“喜欢书法”与“不喜欢书法”的人数之差的绝对值为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
喜欢书法 | 不喜欢书法 | 总计 | |
男学生 | 24 | 32 | 56 |
女学生 | 16 | 24 | 40 |
总计 | 40 | 56 | 96 |
附:
 ,显著性水平取0.05,
,显著性水平取0.05, .
.(2)现从上述96人中,按是否喜欢书法采用分层抽样的方法抽取12人进行问卷调查.若从这12人中任选4人,记“喜欢书法”与“不喜欢书法”的人数之差的绝对值为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
您最近一年使用:0次
解题方法
6 . 已知集合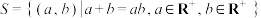 ,
,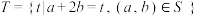 ,则有( )
,则有( )
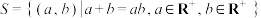 ,
,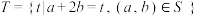 ,则有( )
,则有( )A.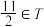 | B.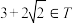 |
C.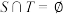 | D.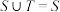 |
您最近一年使用:0次
7 . 某大学举行了百科知识竞赛,为了解此次竞赛成绩的情况,随机抽取部分参赛学生的成绩,整理并制作出如下不完整的统计表和统计图,请根据图表信息解答以下问题:
 __________;
__________;
(2)补全频数分布直方图;
(3)计算扇形统计图中“C”对应的圆心角度数;
(4)该大学共有240人参加竞赛,若成绩在80分以上(包括80分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数?
组别 | 成绩x/分 | 频数 |
A组 |
| a |
B组 |
| 12 |
C组 |
| 8 |
D组 |
| 6 |
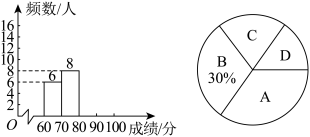
 __________;
__________;(2)补全频数分布直方图;
(3)计算扇形统计图中“C”对应的圆心角度数;
(4)该大学共有240人参加竞赛,若成绩在80分以上(包括80分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数?
您最近一年使用:0次
8 . 某工厂在春节期间为职工举办了趣味有奖灯谜活动,有6个灯谜,编号为: 个灯谜中猜对1个获“小奖”,猜对3个获“中奖”,猜对6个获“大奖”.
个灯谜中猜对1个获“小奖”,猜对3个获“中奖”,猜对6个获“大奖”.
(1)小王从6个灯谜中任取3个作答,设选中编号为 的灯谜的个数为随机变量X,求X的分布列及数学期望;
的灯谜的个数为随机变量X,求X的分布列及数学期望;
(2)若小王猜对任一编号灯谜的概率为 ,求小王在猜对编号为
,求小王在猜对编号为 的灯谜的条件下,获得“中奖”的概率.
的灯谜的条件下,获得“中奖”的概率.
 个灯谜中猜对1个获“小奖”,猜对3个获“中奖”,猜对6个获“大奖”.
个灯谜中猜对1个获“小奖”,猜对3个获“中奖”,猜对6个获“大奖”.(1)小王从6个灯谜中任取3个作答,设选中编号为
 的灯谜的个数为随机变量X,求X的分布列及数学期望;
的灯谜的个数为随机变量X,求X的分布列及数学期望;(2)若小王猜对任一编号灯谜的概率为
 ,求小王在猜对编号为
,求小王在猜对编号为 的灯谜的条件下,获得“中奖”的概率.
的灯谜的条件下,获得“中奖”的概率.
您最近一年使用:0次
9 . 某市对确诊病例在地区实行区域管控,严格履行疫情防控措施.为防范疫情,某校欲购置规格分别为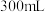 和
和 的甲、乙两种消毒液若干瓶,已知购买2瓶甲种和1瓶乙种消毒液需要61元,购买3瓶甲种和4瓶乙种消毒液需要154元.求甲、乙两种消毒液的单价.
的甲、乙两种消毒液若干瓶,已知购买2瓶甲种和1瓶乙种消毒液需要61元,购买3瓶甲种和4瓶乙种消毒液需要154元.求甲、乙两种消毒液的单价.
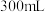 和
和 的甲、乙两种消毒液若干瓶,已知购买2瓶甲种和1瓶乙种消毒液需要61元,购买3瓶甲种和4瓶乙种消毒液需要154元.求甲、乙两种消毒液的单价.
的甲、乙两种消毒液若干瓶,已知购买2瓶甲种和1瓶乙种消毒液需要61元,购买3瓶甲种和4瓶乙种消毒液需要154元.求甲、乙两种消毒液的单价.
您最近一年使用:0次
10 . 河汉湖素有鱼米之乡的美誉,某水产养殖大户为了更好地发挥技术优势,一次性收购了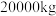 淡水鱼,计划养殖一段时间后再出售.若每天放养的费用均为400元,收购成本为300000元.设这批淡水鱼放养t天后的质量为m(
淡水鱼,计划养殖一段时间后再出售.若每天放养的费用均为400元,收购成本为300000元.设这批淡水鱼放养t天后的质量为m(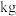 ),销售单价为y元/
),销售单价为y元/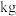 .根据以往经验可知:m与t的函数关系为
.根据以往经验可知:m与t的函数关系为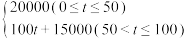 ,y与t的函数关系如图所示.
,y与t的函数关系如图所示.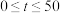 和
和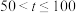 时,y与t的函数关系式;
时,y与t的函数关系式;
(2)设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润 销售总额
销售总额 总成本)
总成本)
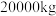 淡水鱼,计划养殖一段时间后再出售.若每天放养的费用均为400元,收购成本为300000元.设这批淡水鱼放养t天后的质量为m(
淡水鱼,计划养殖一段时间后再出售.若每天放养的费用均为400元,收购成本为300000元.设这批淡水鱼放养t天后的质量为m(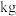 ),销售单价为y元/
),销售单价为y元/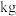 .根据以往经验可知:m与t的函数关系为
.根据以往经验可知:m与t的函数关系为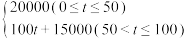 ,y与t的函数关系如图所示.
,y与t的函数关系如图所示.
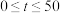 和
和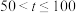 时,y与t的函数关系式;
时,y与t的函数关系式;(2)设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润
 销售总额
销售总额 总成本)
总成本)
您最近一年使用:0次