解题方法
1 . 在刚刚结束的巴黎奥运会中,国球选手再创辉煌,包揽全部5枚金牌,其中最惊险激烈的就是男单 决赛,中国选手樊振东对战日本选手张本智和.比赛采取7局4胜制,每局为11分制,每赢一球得一分.
决赛,中国选手樊振东对战日本选手张本智和.比赛采取7局4胜制,每局为11分制,每赢一球得一分.
(1)樊振东首局失利,第二局比赛双方打到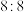 平,此时张本智和连续发球2次,然后樊振东连续发球2次.根据以往比赛结果统计,樊振东发球时他自己得分的概率为0.6,张本智和发球时樊振东得分的概率为0.5,每次发球的结果相互独立,令人遗㙳的是该局比赛结果,樊振东最终以9:11落败,求其以该比分落败的概率;
平,此时张本智和连续发球2次,然后樊振东连续发球2次.根据以往比赛结果统计,樊振东发球时他自己得分的概率为0.6,张本智和发球时樊振东得分的概率为0.5,每次发球的结果相互独立,令人遗㙳的是该局比赛结果,樊振东最终以9:11落败,求其以该比分落败的概率;
(2)在本场比赛中,张本智和先以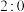 领先.根据以往比赛结果统计,在后续的每局比赛中樊振东获胜的概率为
领先.根据以往比赛结果统计,在后续的每局比赛中樊振东获胜的概率为 ,张本智和获胜的概率为
,张本智和获胜的概率为 ,且每局比赛的结果相互独立.假设两人又进行了
,且每局比赛的结果相互独立.假设两人又进行了 局后比赛结束,求
局后比赛结束,求 的分布列与数学期望
的分布列与数学期望
 决赛,中国选手樊振东对战日本选手张本智和.比赛采取7局4胜制,每局为11分制,每赢一球得一分.
决赛,中国选手樊振东对战日本选手张本智和.比赛采取7局4胜制,每局为11分制,每赢一球得一分.(1)樊振东首局失利,第二局比赛双方打到
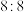 平,此时张本智和连续发球2次,然后樊振东连续发球2次.根据以往比赛结果统计,樊振东发球时他自己得分的概率为0.6,张本智和发球时樊振东得分的概率为0.5,每次发球的结果相互独立,令人遗㙳的是该局比赛结果,樊振东最终以9:11落败,求其以该比分落败的概率;
平,此时张本智和连续发球2次,然后樊振东连续发球2次.根据以往比赛结果统计,樊振东发球时他自己得分的概率为0.6,张本智和发球时樊振东得分的概率为0.5,每次发球的结果相互独立,令人遗㙳的是该局比赛结果,樊振东最终以9:11落败,求其以该比分落败的概率;(2)在本场比赛中,张本智和先以
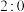 领先.根据以往比赛结果统计,在后续的每局比赛中樊振东获胜的概率为
领先.根据以往比赛结果统计,在后续的每局比赛中樊振东获胜的概率为 ,张本智和获胜的概率为
,张本智和获胜的概率为 ,且每局比赛的结果相互独立.假设两人又进行了
,且每局比赛的结果相互独立.假设两人又进行了 局后比赛结束,求
局后比赛结束,求 的分布列与数学期望
的分布列与数学期望
您最近一年使用:0次
名校
解题方法
2 . 某学校高二年级乒乓球社团举办了一次乒乓球比赛,进入决赛的9名选手来自于3个不同的班级,三个班级的选手人数分别是2,3,4,本次决赛的比赛赛制采取单循环方式,即每名选手进行8场比赛,每场比赛采取5局3胜制,先赢得三场的人为获胜者,比赛结束,根据积分选出最后的冠军.如果最终积分相同,则同分选手加赛决出排名,积分规则如下:比赛中以3:0或3:1取胜的选手积3分,失败的选手积0分;而在比赛中以3:2取胜的选手积2分,失败的选手积1分.已知第6场是甲、乙之间的比赛,设每局比赛甲取胜的概率为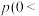
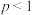 ).
).
(1)若进入决赛的9名选手获得冠亚军的概率相等,则比赛结束后冠亚军恰好来自同一个班级的概率是多少?
(2)在第6场比赛中,当 时,设甲所得积分为
时,设甲所得积分为 ,求
,求 的分布列及期望.
的分布列及期望.
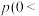
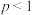 ).
).(1)若进入决赛的9名选手获得冠亚军的概率相等,则比赛结束后冠亚军恰好来自同一个班级的概率是多少?
(2)在第6场比赛中,当
 时,设甲所得积分为
时,设甲所得积分为 ,求
,求 的分布列及期望.
的分布列及期望.
您最近一年使用:0次
解题方法
3 . 一个袋子里装有除颜色以外完全相同的白球和黑球共10个,其中白球有4个,黑球有6个.
(1)若有放回地从袋中随机摸出3个球,求恰好摸到2个黑球的概率;
(2)若不放回地从袋中随机摸出2个球,用 表示摸出的黑球个数,求
表示摸出的黑球个数,求 的分布列和期望与方差.
的分布列和期望与方差.
(1)若有放回地从袋中随机摸出3个球,求恰好摸到2个黑球的概率;
(2)若不放回地从袋中随机摸出2个球,用
 表示摸出的黑球个数,求
表示摸出的黑球个数,求 的分布列和期望与方差.
的分布列和期望与方差.
您最近一年使用:0次
名校
4 . 某汽车销售公司为了提升公司的业绩,将最近一段时间内每日的汽车销售情况进行了统计,如图所示. 的值,并求该公司这段时间内每日汽车销售量的第60百分位数;
的值,并求该公司这段时间内每日汽车销售量的第60百分位数;
(2)以频率估计概率,若在这段时间内随机选择4天,设每日汽车销售量在 内的天数为
内的天数为 ,在恰有1天的汽车销售量不超过150辆的条件下,求
,在恰有1天的汽车销售量不超过150辆的条件下,求 的分布列及数学期望;
的分布列及数学期望;
(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:在三棱锥 中,
中, 、
、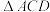 均是边长为2的正三角形,
均是边长为2的正三角形,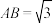 ,现从写有数字1~8的八个标签中随机选择两个分别贴在
,现从写有数字1~8的八个标签中随机选择两个分别贴在 、
、 两个顶点,记顶点
两个顶点,记顶点 、
、 上的数字分别为
上的数字分别为 和
和 ,若
,若 为侧棱
为侧棱 上一个动点,满足
上一个动点,满足 ,当“二面角
,当“二面角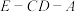 大于
大于 ”即为中奖,求中奖的概率.
”即为中奖,求中奖的概率.

 的值,并求该公司这段时间内每日汽车销售量的第60百分位数;
的值,并求该公司这段时间内每日汽车销售量的第60百分位数;(2)以频率估计概率,若在这段时间内随机选择4天,设每日汽车销售量在
 内的天数为
内的天数为 ,在恰有1天的汽车销售量不超过150辆的条件下,求
,在恰有1天的汽车销售量不超过150辆的条件下,求 的分布列及数学期望;
的分布列及数学期望;(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:在三棱锥
 中,
中, 、
、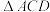 均是边长为2的正三角形,
均是边长为2的正三角形,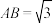 ,现从写有数字1~8的八个标签中随机选择两个分别贴在
,现从写有数字1~8的八个标签中随机选择两个分别贴在 、
、 两个顶点,记顶点
两个顶点,记顶点 、
、 上的数字分别为
上的数字分别为 和
和 ,若
,若 为侧棱
为侧棱 上一个动点,满足
上一个动点,满足 ,当“二面角
,当“二面角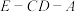 大于
大于 ”即为中奖,求中奖的概率.
”即为中奖,求中奖的概率.
您最近一年使用:0次
解题方法
5 . 如图:一张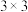 的棋盘,横行编号
的棋盘,横行编号 :竖排编号
:竖排编号 .一颗棋子目前位于棋盘的
.一颗棋子目前位于棋盘的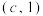 处,它的移动规则是:每次移动到与自身所在格不相邻的异色格中.例如该棋子第一次移动可以从
处,它的移动规则是:每次移动到与自身所在格不相邻的异色格中.例如该棋子第一次移动可以从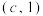 移动到
移动到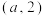 或
或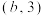 .棋子每次移动到不同目的地间的概率均为
.棋子每次移动到不同目的地间的概率均为 .
.
②假设棋子两次移动后,最终停留到第1,2,3行时,分别能获得 分,设得分为
分,设得分为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(2)现在于棋盘左下角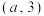 处加入一颗棋子,他们运动规则相同,并且每次移动同时行动.移动
处加入一颗棋子,他们运动规则相同,并且每次移动同时行动.移动 次后,两棋子位于同一格的概率为
次后,两棋子位于同一格的概率为 ,求
,求 的通项公式.
的通项公式.
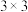 的棋盘,横行编号
的棋盘,横行编号 :竖排编号
:竖排编号 .一颗棋子目前位于棋盘的
.一颗棋子目前位于棋盘的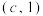 处,它的移动规则是:每次移动到与自身所在格不相邻的异色格中.例如该棋子第一次移动可以从
处,它的移动规则是:每次移动到与自身所在格不相邻的异色格中.例如该棋子第一次移动可以从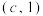 移动到
移动到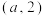 或
或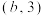 .棋子每次移动到不同目的地间的概率均为
.棋子每次移动到不同目的地间的概率均为 .
.
②假设棋子两次移动后,最终停留到第1,2,3行时,分别能获得
 分,设得分为
分,设得分为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.(2)现在于棋盘左下角
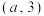 处加入一颗棋子,他们运动规则相同,并且每次移动同时行动.移动
处加入一颗棋子,他们运动规则相同,并且每次移动同时行动.移动 次后,两棋子位于同一格的概率为
次后,两棋子位于同一格的概率为 ,求
,求 的通项公式.
的通项公式.
您最近一年使用:0次
解题方法
6 . 如图,一个质点在随机外力作用下,从原点O处出发,每次等可能地向左或者向右移动一个单位.
(2)设移动5次中向右移动的次数为X,求X的分布列和期望.
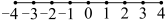
(2)设移动5次中向右移动的次数为X,求X的分布列和期望.
您最近一年使用:0次
7 . 袋子中装有5个白球和3个红球,现从袋子中不放回地摸取4个球,取到1个白球得2分,取到1个红球得1分,设摸球所得分数之和为随机变量 .
.
(1)求摸球得分不低于6分的概率;
(2)求摸球所得分数之和的方差.
 .
.(1)求摸球得分不低于6分的概率;
(2)求摸球所得分数之和的方差.
您最近一年使用:0次
8 . 随着“绿水青山就是金山银山”的环保理念不断深入人心,某地区相关部门实施了对当地现有水库及湖泊的环境改造,从而进一步提高了水中生物的生存环境,改善了当地的生态环境,为了调查某湖泊的环境保护情况,在该湖泊中随机捕捞了50条鱼进行称重,经过相关人员对数据的整理和分析发现鱼的重量 (单位:kg)近似服从以2为数学期望的正态分布.
(单位:kg)近似服从以2为数学期望的正态分布.
(1)已知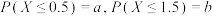 ,在该湖泊中随机捕捞一条鱼,求鱼的重量在
,在该湖泊中随机捕捞一条鱼,求鱼的重量在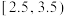 的概率;
的概率;
(2)①若从捕捞的50条鱼中随机挑出6条鱼进行称重,得到的数据如下表所示:
现从这6条鱼中随机选3条,设其重量在 的条数为
的条数为 ,求
,求 的数学期望;
的数学期望;
②为了获得更大的经济效益,当地渔民计划购买一批饲料对水体中的鱼进行喂养,试从数学建模的观点分析如何才能达到经济效益的最大化?
 (单位:kg)近似服从以2为数学期望的正态分布.
(单位:kg)近似服从以2为数学期望的正态分布.(1)已知
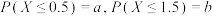 ,在该湖泊中随机捕捞一条鱼,求鱼的重量在
,在该湖泊中随机捕捞一条鱼,求鱼的重量在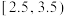 的概率;
的概率;(2)①若从捕捞的50条鱼中随机挑出6条鱼进行称重,得到的数据如下表所示:
重量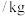 |  |  | 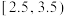 |
| 条数 | 3 | 1 | 2 |
 的条数为
的条数为 ,求
,求 的数学期望;
的数学期望;②为了获得更大的经济效益,当地渔民计划购买一批饲料对水体中的鱼进行喂养,试从数学建模的观点分析如何才能达到经济效益的最大化?
您最近一年使用:0次
名校
9 . 重庆市高考数学自 年起第
年起第 至
至 题为多选题,每道题共
题为多选题,每道题共 个选项,正确选项为两个或三个,其评分标准是:每道题满分
个选项,正确选项为两个或三个,其评分标准是:每道题满分 分,全部选对得
分,全部选对得 分,部分选对得部分分(若某道题正确选项为两个,漏选一个正确选项得
分,部分选对得部分分(若某道题正确选项为两个,漏选一个正确选项得 分;若某道题正确选项为三个,漏选一个正确选项得
分;若某道题正确选项为三个,漏选一个正确选项得 分,漏选两个正确选项得
分,漏选两个正确选项得 分),错选或不选得
分),错选或不选得 分.现甲、乙两名同学参加了有这种多选题的某次模拟考试.
分.现甲、乙两名同学参加了有这种多选题的某次模拟考试.
(1)假设第 题正确选项为三个,若甲同学完全不会,就随机地选了两项或三项作答,所有选法等可能,求甲同学第
题正确选项为三个,若甲同学完全不会,就随机地选了两项或三项作答,所有选法等可能,求甲同学第 题得
题得 分的概率;
分的概率;
(2)已知第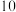 题乙同学能正确的判断出其中的一个选项是不符合题意的,他在剩下的三个选项中随机地猜选了两个选项;第
题乙同学能正确的判断出其中的一个选项是不符合题意的,他在剩下的三个选项中随机地猜选了两个选项;第 题乙同学完全不会,他在四个选项中随机地猜选了一个选项.若第
题乙同学完全不会,他在四个选项中随机地猜选了一个选项.若第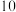 题和
题和 题正确选项是两个和三个的概率都为
题正确选项是两个和三个的概率都为 .求乙同学第
.求乙同学第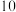 题和
题和 题得分总和
题得分总和 的分布列及数学期望.
的分布列及数学期望.
 年起第
年起第 至
至 题为多选题,每道题共
题为多选题,每道题共 个选项,正确选项为两个或三个,其评分标准是:每道题满分
个选项,正确选项为两个或三个,其评分标准是:每道题满分 分,全部选对得
分,全部选对得 分,部分选对得部分分(若某道题正确选项为两个,漏选一个正确选项得
分,部分选对得部分分(若某道题正确选项为两个,漏选一个正确选项得 分;若某道题正确选项为三个,漏选一个正确选项得
分;若某道题正确选项为三个,漏选一个正确选项得 分,漏选两个正确选项得
分,漏选两个正确选项得 分),错选或不选得
分),错选或不选得 分.现甲、乙两名同学参加了有这种多选题的某次模拟考试.
分.现甲、乙两名同学参加了有这种多选题的某次模拟考试.(1)假设第
 题正确选项为三个,若甲同学完全不会,就随机地选了两项或三项作答,所有选法等可能,求甲同学第
题正确选项为三个,若甲同学完全不会,就随机地选了两项或三项作答,所有选法等可能,求甲同学第 题得
题得 分的概率;
分的概率;(2)已知第
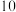 题乙同学能正确的判断出其中的一个选项是不符合题意的,他在剩下的三个选项中随机地猜选了两个选项;第
题乙同学能正确的判断出其中的一个选项是不符合题意的,他在剩下的三个选项中随机地猜选了两个选项;第 题乙同学完全不会,他在四个选项中随机地猜选了一个选项.若第
题乙同学完全不会,他在四个选项中随机地猜选了一个选项.若第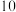 题和
题和 题正确选项是两个和三个的概率都为
题正确选项是两个和三个的概率都为 .求乙同学第
.求乙同学第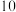 题和
题和 题得分总和
题得分总和 的分布列及数学期望.
的分布列及数学期望.
您最近一年使用:0次
名校
10 . 为响应国家使用新能源的号召,促进“碳达峰碳中和”的目标实现,某汽车生产企业在积极上市四款新能源汽车后,对它们进行了市场调研.该企业研发部门从购买这四款车的车主中随机抽取了 人,让车主对所购汽车的性能进行评分,每款车的性能都有
人,让车主对所购汽车的性能进行评分,每款车的性能都有 分、
分、 分、
分、 分、
分、 分、
分、 分五个等级,各评分及相应人数的统计结果如下表.
分五个等级,各评分及相应人数的统计结果如下表.
(1)求所抽车主对这四款车性能评分的平均数和第 百分位数;
百分位数;
(2)当评分不小于 时,认为该款车性能优秀,否则认为性能一般.根据上述样本数据,完成上面列联表,并依据
时,认为该款车性能优秀,否则认为性能一般.根据上述样本数据,完成上面列联表,并依据 的独立性检验,能否认为汽车的性能与款式有关?
的独立性检验,能否认为汽车的性能与款式有关?
(3)为提高这四款新车的性能,现从样本评分不大于 的基础版车主中,随机抽取
的基础版车主中,随机抽取 人征求意见,记
人征求意见,记 为其中基础版
为其中基础版 车主的人数,求
车主的人数,求 的分布列及数学期望.
的分布列及数学期望.
附: .
.
 人,让车主对所购汽车的性能进行评分,每款车的性能都有
人,让车主对所购汽车的性能进行评分,每款车的性能都有 分、
分、 分、
分、 分、
分、 分、
分、 分五个等级,各评分及相应人数的统计结果如下表.
分五个等级,各评分及相应人数的统计结果如下表.| 汽车性能 | 汽车款式 | 合计 | ||||
| 基础版 | 豪华版 | |||||
| 一般 | ||||||
| 优秀 | ||||||
| 合计 | ||||||
性能评分 汽车款式 |
|
|
|
|
| |
基础版 | 基础版 |
|
|
|
|
|
基础版 |
|
|
|
|
| |
豪华版 | 豪华版 |
|
|
|
|
|
豪华版 |
|
|
|
|
| |
(1)求所抽车主对这四款车性能评分的平均数和第
 百分位数;
百分位数;(2)当评分不小于
 时,认为该款车性能优秀,否则认为性能一般.根据上述样本数据,完成上面列联表,并依据
时,认为该款车性能优秀,否则认为性能一般.根据上述样本数据,完成上面列联表,并依据 的独立性检验,能否认为汽车的性能与款式有关?
的独立性检验,能否认为汽车的性能与款式有关?(3)为提高这四款新车的性能,现从样本评分不大于
 的基础版车主中,随机抽取
的基础版车主中,随机抽取 人征求意见,记
人征求意见,记 为其中基础版
为其中基础版 车主的人数,求
车主的人数,求 的分布列及数学期望.
的分布列及数学期望.附:
 .
.
|
|
|
|
|
|
|
|
|
|
您最近一年使用:0次













