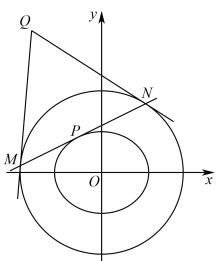
1 . 如图,P为椭圆
 上的动点,过P作椭圆
上的动点,过P作椭圆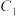 的切线交圆
的切线交圆
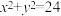 于M,N,过M,N作
于M,N,过M,N作 切线交于Q,则Q的轨迹方程为
切线交于Q,则Q的轨迹方程为_______________ ; 的最大值为
的最大值为_________________ .

 上的动点,过P作椭圆
上的动点,过P作椭圆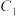 的切线交圆
的切线交圆
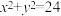 于M,N,过M,N作
于M,N,过M,N作 切线交于Q,则Q的轨迹方程为
切线交于Q,则Q的轨迹方程为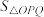 的最大值为
的最大值为
您最近一年使用:0次
2 . 设椭圆 的右焦点为
的右焦点为 ,离心率为
,离心率为 ,
, 为圆
为圆 :
: 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆左焦点 的直线
的直线 (斜率存在且不为0)交椭圆于
(斜率存在且不为0)交椭圆于 ,
, 两点,过
两点,过 且与
且与 垂直的直线
垂直的直线 与圆
与圆 交于
交于 ,
, 两点,求四边形
两点,求四边形 面积的取值范围.
面积的取值范围.
 的右焦点为
的右焦点为 ,离心率为
,离心率为 ,
, 为圆
为圆 :
: 的圆心.
的圆心.(1)求椭圆的方程;
(2)已知过椭圆左焦点
 的直线
的直线 (斜率存在且不为0)交椭圆于
(斜率存在且不为0)交椭圆于 ,
, 两点,过
两点,过 且与
且与 垂直的直线
垂直的直线 与圆
与圆 交于
交于 ,
, 两点,求四边形
两点,求四边形 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
2022-04-15更新
|
532次组卷
|
2卷引用:黑龙江省齐齐哈尔市恒昌中学校2021-2022学年高二上学期期中考试数学试题
3 . 已知椭圆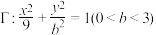 的左右焦点为
的左右焦点为 ,
, ,
, 是椭圆上半部分的动点,连接
是椭圆上半部分的动点,连接 和长轴的左右两个端点所得两直线交
和长轴的左右两个端点所得两直线交 轴的正半轴于A,
轴的正半轴于A, 两点
两点 点A在
点A在 的上方或重合
的上方或重合 .
.
(1)当 时,若B是线段OA的中点,求直线MA的方程;
时,若B是线段OA的中点,求直线MA的方程;
(2)当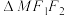 面积
面积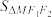 最大时,求椭圆的方程;
最大时,求椭圆的方程;
(3)当 时,在
时,在 轴上是否存在点
轴上是否存在点 使得
使得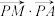 为定值,若存在,求
为定值,若存在,求 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
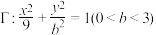 的左右焦点为
的左右焦点为 ,
, ,
, 是椭圆上半部分的动点,连接
是椭圆上半部分的动点,连接 和长轴的左右两个端点所得两直线交
和长轴的左右两个端点所得两直线交 轴的正半轴于A,
轴的正半轴于A, 两点
两点 点A在
点A在 的上方或重合
的上方或重合 .
.(1)当
 时,若B是线段OA的中点,求直线MA的方程;
时,若B是线段OA的中点,求直线MA的方程;(2)当
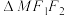 面积
面积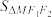 最大时,求椭圆的方程;
最大时,求椭圆的方程;(3)当
 时,在
时,在 轴上是否存在点
轴上是否存在点 使得
使得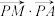 为定值,若存在,求
为定值,若存在,求 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
您最近一年使用:0次
2021·全国·模拟预测
解题方法
4 . 已知椭圆C: 的离心率为
的离心率为 ,
, ,
, 分别为椭圆C的左、右焦点,过
分别为椭圆C的左、右焦点,过 且与x轴垂直的直线与椭圆C交于点A,B,且
且与x轴垂直的直线与椭圆C交于点A,B,且 的面积为
的面积为 .
.
(1)求椭圆C的标准方程;
(2)设直线l与椭圆C交于不同于右顶点P的M,N两点,且 ,求
,求 的最大值.
的最大值.
 的离心率为
的离心率为 ,
, ,
, 分别为椭圆C的左、右焦点,过
分别为椭圆C的左、右焦点,过 且与x轴垂直的直线与椭圆C交于点A,B,且
且与x轴垂直的直线与椭圆C交于点A,B,且 的面积为
的面积为 .
.(1)求椭圆C的标准方程;
(2)设直线l与椭圆C交于不同于右顶点P的M,N两点,且
 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
5 . 已知圆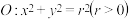 过点
过点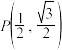 .
.
(1)求圆 的方程;
的方程;
(2)已知点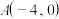 ,
, ,点
,点 是圆
是圆 上任意一点,求
上任意一点,求 的最大值,并求出此时点
的最大值,并求出此时点 的坐标.
的坐标.
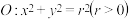 过点
过点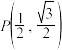 .
.(1)求圆
 的方程;
的方程;(2)已知点
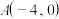 ,
, ,点
,点 是圆
是圆 上任意一点,求
上任意一点,求 的最大值,并求出此时点
的最大值,并求出此时点 的坐标.
的坐标.
您最近一年使用:0次
2021-12-24更新
|
669次组卷
|
2卷引用:贵州省2021-2022学年高二12月学业水平考试数学试题
名校
解题方法
6 . O为坐标原点椭圆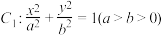 的左右焦点分别为
的左右焦点分别为 ,离心率为
,离心率为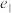 ;双曲线
;双曲线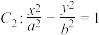 的左右焦点分别为
的左右焦点分别为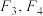 ,离心率为
,离心率为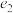 ,已知
,已知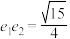 ,切
,切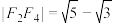 .
.
(1)求 的方程;
的方程;
(2)过 作
作 的不垂直于y轴的弦
的不垂直于y轴的弦 ,M为
,M为 的中点,当直线
的中点,当直线 与
与 交于P,Q两点时,求四边形
交于P,Q两点时,求四边形 面积的最小值.
面积的最小值.
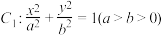 的左右焦点分别为
的左右焦点分别为 ,离心率为
,离心率为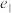 ;双曲线
;双曲线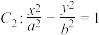 的左右焦点分别为
的左右焦点分别为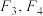 ,离心率为
,离心率为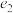 ,已知
,已知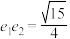 ,切
,切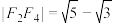 .
.(1)求
 的方程;
的方程;(2)过
 作
作 的不垂直于y轴的弦
的不垂直于y轴的弦 ,M为
,M为 的中点,当直线
的中点,当直线 与
与 交于P,Q两点时,求四边形
交于P,Q两点时,求四边形 面积的最小值.
面积的最小值.
您最近一年使用:0次
2021-11-22更新
|
1714次组卷
|
5卷引用:江苏省徐州市第一中学2021-2022学年高二上学期期中数学试题
江苏省徐州市第一中学2021-2022学年高二上学期期中数学试题(已下线)考点42 圆锥曲线中的范围与最值问题-备战2022年高考数学典型试题解读与变式(已下线)专题30 圆锥曲线三角形面积与四边形面积题型全归类-2(已下线)3.2.2 双曲线的几何性质(难点)-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)(已下线)重难点突破17 圆锥曲线中参数范围与最值问题(八大题型)
名校
解题方法
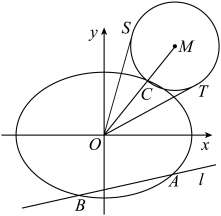
7 . 1.在平面直角坐标系 中,椭圆
中,椭圆 :
: 的离心率为
的离心率为 ,焦距为2.
,焦距为2.
(1)求椭圆 的方程;
的方程;
(2)如图,动直线 :
: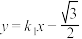 交椭圆
交椭圆 于A,
于A, 两点,
两点, 是椭圆
是椭圆 上一点,直线
上一点,直线 的斜率为
的斜率为 ,且
,且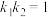 ,
, 是线段
是线段 延长线上一点,且
延长线上一点,且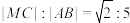 ,
,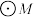 的半径为
的半径为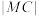 ,
,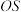 ,
,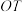 是
是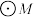 的两条切线,切点分别为S,
的两条切线,切点分别为S, .求
.求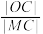 的最小值及
的最小值及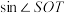 的最大值.
的最大值.
 中,椭圆
中,椭圆 :
: 的离心率为
的离心率为 ,焦距为2.
,焦距为2.
(1)求椭圆
 的方程;
的方程;(2)如图,动直线
 :
: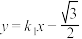 交椭圆
交椭圆 于A,
于A, 两点,
两点, 是椭圆
是椭圆 上一点,直线
上一点,直线 的斜率为
的斜率为 ,且
,且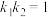 ,
, 是线段
是线段 延长线上一点,且
延长线上一点,且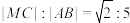 ,
,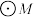 的半径为
的半径为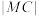 ,
,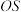 ,
,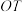 是
是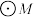 的两条切线,切点分别为S,
的两条切线,切点分别为S, .求
.求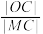 的最小值及
的最小值及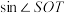 的最大值.
的最大值.
您最近一年使用:0次
2021-11-14更新
|
1573次组卷
|
5卷引用:安徽省六安市第一中学2021-2022学年高二上学期期中数学试题
8 . 1.线段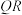 的长等于3,两端点Q、R分别在x轴和y轴上滑动,点S在线段QR上,且
的长等于3,两端点Q、R分别在x轴和y轴上滑动,点S在线段QR上,且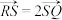 ,点S的轨迹为曲线C.
,点S的轨迹为曲线C.
(1)求曲线C的方程
(2)曲线C与x轴相交于A、B两点,P为曲线C上一动点,直线PA,PB与直线 交于M,N两点,
交于M,N两点, 与
与 的外接圆的周长分别为
的外接圆的周长分别为 ,
, ,求
,求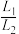 的最小值.
的最小值.
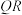 的长等于3,两端点Q、R分别在x轴和y轴上滑动,点S在线段QR上,且
的长等于3,两端点Q、R分别在x轴和y轴上滑动,点S在线段QR上,且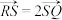 ,点S的轨迹为曲线C.
,点S的轨迹为曲线C.(1)求曲线C的方程
(2)曲线C与x轴相交于A、B两点,P为曲线C上一动点,直线PA,PB与直线
 交于M,N两点,
交于M,N两点, 与
与 的外接圆的周长分别为
的外接圆的周长分别为 ,
, ,求
,求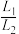 的最小值.
的最小值.
您最近一年使用:0次
2021-11-12更新
|
1139次组卷
|
7卷引用:四川省成都市树德中学2021届高三高考适应性考试数学(文)试题
四川省成都市树德中学2021届高三高考适应性考试数学(文)试题四川省成都市树德中学2021届高三高考适应性考试数学(理)试题新疆喀什市部分学校2022届高三全真模拟数学试题(已下线)专题07 不等式与线性规划-备战2022年高考数学(文)母题题源解密(全国乙卷)(已下线)考点38 椭圆-备战2022年高考数学典型试题解读与变式(已下线)考点42 圆锥曲线中的范围与最值问题-备战2022年高考数学典型试题解读与变式(已下线)专题26 圆锥曲线(理科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲
9 . 椭圆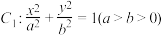 经过点
经过点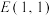 ,其右焦点为抛物线
,其右焦点为抛物线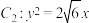 的焦点
的焦点 ;直线
;直线 与椭圆
与椭圆 交于
交于 ,
, 两点,且以
两点,且以 为直径的圆过原点.
为直径的圆过原点.

(1)求椭圆 的方程;
的方程;
(2)若过原点的直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ,求四边形
,求四边形 面积的最大值.
面积的最大值.
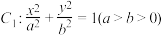 经过点
经过点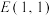 ,其右焦点为抛物线
,其右焦点为抛物线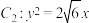 的焦点
的焦点 ;直线
;直线 与椭圆
与椭圆 交于
交于 ,
, 两点,且以
两点,且以 为直径的圆过原点.
为直径的圆过原点.
(1)求椭圆
 的方程;
的方程;(2)若过原点的直线
 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ,求四边形
,求四边形 面积的最大值.
面积的最大值.
您最近一年使用:0次
名校
解题方法
10 . 1.已知椭圆 ),离心率为
),离心率为 ,如图,
,如图, 是圆M:
是圆M: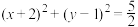 的一条直径,若椭圆E经过A、B两点.
的一条直径,若椭圆E经过A、B两点.

(1)求椭圆E的方程.
(2)点P为椭圆E上一个动点,求△ 面积的最大值.
面积的最大值.
 ),离心率为
),离心率为 ,如图,
,如图, 是圆M:
是圆M: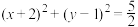 的一条直径,若椭圆E经过A、B两点.
的一条直径,若椭圆E经过A、B两点.
(1)求椭圆E的方程.
(2)点P为椭圆E上一个动点,求△
 面积的最大值.
面积的最大值.
您最近一年使用:0次



